IBDP Maths AA: Topic: SL 4.2: Presentation of data: IB style Questions SL Paper 1

IB DP PhysicsIB DP MathsIB DP ChemistryIB DP Biology

IB DP Maths AA : SL Paper -1 : All Topics

Question

On a Monday at an amusement park, a sample of 40 visitors was randomly selected as they were leaving the park. They were asked how many times that day they had been on a ride called The Dragon. This information is summarized in the following frequency table.

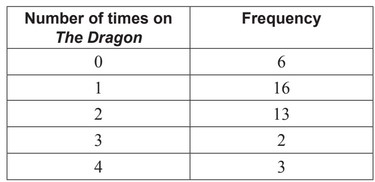
It can be assumed that this sample is representative of all visitors to the park for the following day.

(a) For the following day, Tuesday, estimate
(i) the probability that a randomly selected visitor will ride The Dragon;
(ii) the expected number of times a visitor will ride The Dragon.

It is known that 1000 visitors will attend the amusement park on Tuesday. The Dragon can carry a maximum of 10 people each time it runs.

(b) Estimate the minimum number of times The Dragon must run to satisfy demand.

Answer/Explanation

Answer:

(a) (i) summing frequencies of riders or finding complement
probability = \(\frac{34}{40}\)
(ii) attempt to find expected value
\(\frac{16}{40} + (2 \times \frac{13}{40}) + (3 \times \frac{2}{40}) + (4 \times \frac{3}{40})\)
\(\frac{60}{40}(=1.5)\)

(b) evidence of their rides/visitor \(\times \) 1000 or ÷ 10
1500 OR 0.15
150 (times)

Question

Each athlete on a running team recorded the distance ( M miles) they ran in 30 minutes.

The median distance is 4 miles and the interquartile range is 1.1 miles.

This information is shown in the following box-and-whisker plot.

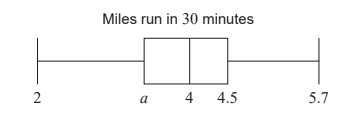
    1. Find the value of a . [2]

      The distance in miles, M , can be converted to the distance in kilometres, K , using the formula K = \(\frac{8}{5}\) .

    2. Write down the value of the median distance in kilometres (km). [1]

      The variance of the distances run by the athletes is \(\frac{16}{9}\) km2 .

      The standard deviation of the distances is b miles.

    3. Find the value of b . [4]

      A total of 600 athletes from different teams compete in a 5 km race. The times the 600 athletes

      took to run the 5 km race are shown in the following cumulative frequency graph.

      There were 400 athletes who took between 22 and m minutes to complete the 5 km race.

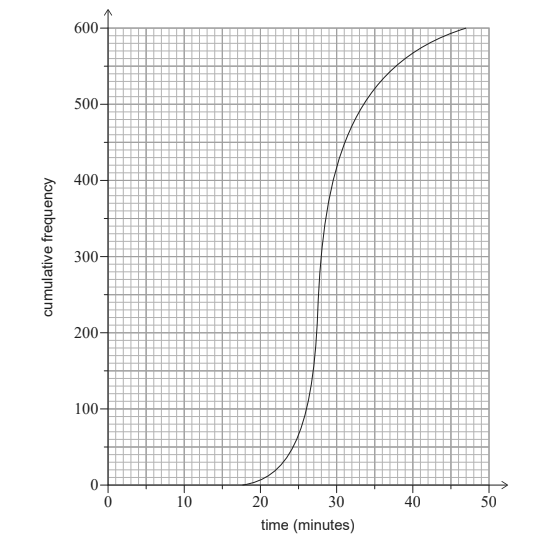
    4. Find m . [3]

      The first 150 athletes that completed the race won a prize.

    5. Given that an athlete took between 22 and m minutes to complete the 5 km race, calculate the probability that they won a prize. [5]

Answer/Explanation

Ans:

  1. (a)
      1. valid approach eg Q3-Q1 , Q3 -1.1, 4.5 – a = 1.1
      2. a = 3.4
  2. (b)\(\frac{32}{5}\)(=6.4)(km)
  3. (c)
    1. METHOD 1 (standard deviation first)
      valid approach
    2. eg standard deviation = \(\sqrt{variance}, \sqrt{\frac{16}{9}}\)
    3. standard deviation = \(\frac{4}{3}\)(km)
    4. valid approach to convert their standard deviation
    5. eg \(\frac{4}{3}\times \frac{5}{8},\sqrt{\frac{16}{9}}= \frac{8}{5}M\)
    6. \(\frac{20}{24}\)(miles)(=\(\frac{5}{6})\)
    7. METHOD 2 (variance first)
    8. valid approach to convert variance
    9. eg \((\frac{5}{8})^{2}, \frac{64}{25},\frac{16}{9}\times (\frac{5}{8})^{2}\)
    10. variance= \(\frac{25}{36}\)
    11. valid approach
    12. eg standard deviation \(\sqrt{variance}, \sqrt{\frac{25}{36}},\sqrt{\frac{16}{9}}\)\(\times (\frac{5}{8})^{2}\)
    13. \(\frac{20}{24}\)(miles)(=\(\frac{5}{6})\)
  4. (d)
    1. correct frequency for 22 minutes
    2. eg 20
    3. adding their frequency (do not accept 22 400
    4. eg 20 + 400 , 420 athletes 
    5. m = 30 (minutes)
  5. (e)
    1. 27 (minutes)
    2. correct working
    3. eg 130 athletes between 22 and 27 minutes, P(22<t<27)= \(\frac{150-20}{600}, \frac{13}{60}\)
    4. evidence of conditional probability or reduced sample space
    5. eg P(A|B),P(t<27|22<t<30), \(\frac{p(22<t<27)}{p(22<t<m)}\), \(\frac{150}{400}\)
    6. correct working
    7. eg \(\frac{\frac{130}{600}}{\frac{400}{600}}, \frac{150-20}{400}\)
    8. \(\frac{130}{400}(\frac{13}{40}= \frac{78000}{240000}= \frac{390}{1200}= 0.325)\)

Question

A box contains 100 cards. Each card has a number between one and six written on it. The following table shows the frequencies for each number.


Calculate the value of k.

[2]
a.

Find

(i)     the median;

(ii)    the interquartile range.

[5]
b(i) and (ii).
Answer/Explanation

Markscheme

evidence of using \(\sum {{f_i} = 100} \)     (M1)

\(k = 4\)     A1     N2

[2 marks]

a.

(i) evidence of median position     (M1)

e.g. 50th item, \(26 + 10 + 20 = 56\)

\({\text{median}} = 3\)     A1     N2

(ii) \({Q_1} = 1\) and \({Q_3} = 5\)     (A1)(A1)

\({\text{interquartile range}} = 4\) (accept 1 to 5 or \(5 – 1\) , etc.)     A1     N3

[5 marks]

b(i) and (ii).

Question

The ages of people attending a music concert are given in the table below.


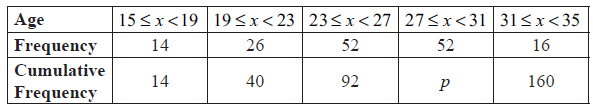
Find p .

[2]
a.

The cumulative frequency diagram is given below.


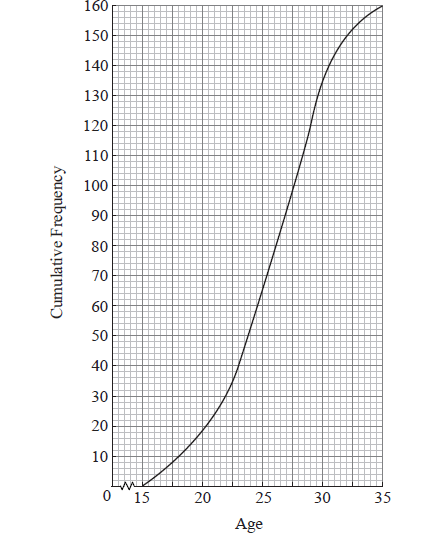
Use the diagram to estimate

(i)     the 80th percentile;

(ii)    the interquartile range.

 

[5]
b(i) and (ii).
Answer/Explanation

Markscheme

evidence of valid approach     (M1)

e.g. \(92 + 52\) , line on graph at \(x = 31\)

\(p = 144\)     A1     N2

[2 marks]

a.

(i) evidence of valid approach     (M1)

e.g. line on graph, \(0.8 \times 160\) , using complement

\( = 29.5\)     A1     N2

(ii) \({Q_1} = 23\) ; \({Q_3} = 29\)      (A1)(A1)

\({\text{IQR}} = 6\) (accept any notation that suggests an interval)     A1     N3

[5 marks]

b(i) and (ii).

Question

[Maximum mark: 5] [without GDC]
The following diagram is a box and whisker plot for a set of data.

The interquartile range is 20 and the range is 40.
(a) Write down the median value.
(b) Find the value of    (i) \(a\);          (ii) \(b\).

Answer/Explanation

(a) 18
(b) (i)   10
(ii)   44

More DP Math AA SL Paper 1 Questions..
Scroll to Top