Question
Aayush places the nine labelled balls shown below into a box.

Aayush then chooses two balls at random, one at a time, from the box. The first ball is not replaced before he chooses the second.
Find the probability that the first ball chosen is
labelled A;
labelled A or labelled N. [2]
Find the probability that the second ball chosen is labelled A, given that the first ball chosen was labelled N. [2]
Find the probability that both balls chosen are labelled N. [2]
Answer/Explanation
Ans:
(a)
(i) \(\frac{3}{9}(\frac{1}{3}\),0.333,0.333333….,33.3%)
(ii)\(\frac{5}{9}\)(0.556,0.555555…,55.6%)
(b)\(\frac{3}{8}\)(0.375,37.5%)
(c)
\(\frac{2}{9}\times \frac{1}{8}\)
\(\frac{2}{72}(\frac{1}{36,}\)0.0278,0.0277777….,2.78%)
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
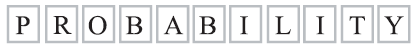
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
Find \({\rm{P}}(A)\) .
Find \({\rm{P}}(B|A)\) .
Find \({\rm{P}}(A \cap B)\) .
Answer/Explanation
Markscheme
\({\rm{P}}(A) = \frac{1}{{11}}\) A1 N1
[1 mark]
\({\rm{P}}(B|A) = \frac{2}{{10}}\) A2 N2
[2 marks]
recognising that \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B|A)\) (M1)
correct values (A1)
e.g. \({\rm{P}}(A \cap B) = \frac{1}{{11}} \times \frac{2}{{10}}\)
\({\rm{P}}(A \cap B) = \frac{2}{{110}}\) A1 N3
[3 marks]
Question
Two boxes contain numbered cards as shown below.
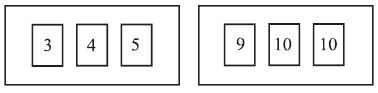
Two cards are drawn at random, one from each box.
Copy and complete the table below to show all nine equally likely outcomes.

Let S be the sum of the numbers on the two cards.
Find the probability of each value of S.
Find the expected value of S.
Anna plays a game where she wins \(\$ 50\) if S is even and loses \(\$ 30\) if S is odd.
Anna plays the game 36 times. Find the amount she expects to have at the end of the 36 games.
Answer/Explanation
Markscheme
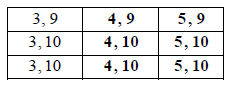 A2 N2
A2 N2
[2 marks]
\({\rm{P}}(12) = \frac{1}{9}\) , \({\rm{P}}(13) = \frac{3}{9}\) , \({\rm{P}}(14) = \frac{3}{9}\) , \({\rm{P}}(15) = \frac{2}{9}\) A2 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) A1
e.g. \({\rm{E}}(S) = 12 \times \frac{1}{9} + 13 \times \frac{3}{9} + 14 \times \frac{3}{9} + 15 \times \frac{2}{9}\)
\({\rm{E}}(S) = \frac{{123}}{9}\) A2 N2
[3 marks]
METHOD 1
correct expression for expected gain E(A) for 1 game (A1)
e.g. \(\frac{4}{9} \times 50 – \frac{5}{9} \times 30\)
\({\rm{E}}(A) = \frac{{50}}{9}\)
amount at end = expected gain for 1 game \( \times 36\) (M1)
= 200 (dollars) A1 N2
METHOD 2
attempt to find expected number of wins and losses (M1)
e.g. \(\frac{4}{9} \times 36\) , \(\frac{5}{9} \times 36\)
attempt to find expected gain E(G) (M1)
e.g. \(16 \times 50 – 30 \times 20\)
\({\text{E}}(G) = 200\) (dollars) A1 N2
[3 marks]
Question
Two boxes contain numbered cards as shown below.

Two cards are drawn at random, one from each box.
Copy and complete the table below to show all nine equally likely outcomes.

Let S be the sum of the numbers on the two cards.
Find the probability of each value of S.
Find the expected value of S.
Anna plays a game where she wins \(\$ 50\) if S is even and loses \(\$ 30\) if S is odd.
Anna plays the game 36 times. Find the amount she expects to have at the end of the 36 games.
Answer/Explanation
Markscheme
 A2 N2
A2 N2
[2 marks]
\({\rm{P}}(12) = \frac{1}{9}\) , \({\rm{P}}(13) = \frac{3}{9}\) , \({\rm{P}}(14) = \frac{3}{9}\) , \({\rm{P}}(15) = \frac{2}{9}\) A2 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) A1
e.g. \({\rm{E}}(S) = 12 \times \frac{1}{9} + 13 \times \frac{3}{9} + 14 \times \frac{3}{9} + 15 \times \frac{2}{9}\)
\({\rm{E}}(S) = \frac{{123}}{9}\) A2 N2
[3 marks]
METHOD 1
correct expression for expected gain E(A) for 1 game (A1)
e.g. \(\frac{4}{9} \times 50 – \frac{5}{9} \times 30\)
\({\rm{E}}(A) = \frac{{50}}{9}\)
amount at end = expected gain for 1 game \( \times 36\) (M1)
= 200 (dollars) A1 N2
METHOD 2
attempt to find expected number of wins and losses (M1)
e.g. \(\frac{4}{9} \times 36\) , \(\frac{5}{9} \times 36\)
attempt to find expected gain E(G) (M1)
e.g. \(16 \times 50 – 30 \times 20\)
\({\text{E}}(G) = 200\) (dollars) A1 N2
[3 marks]
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must play at least one sport from football and rugby.
(i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
Explain why A and B are not mutually exclusive.
Show that A and B are not independent.
Answer/Explanation
Markscheme
(i) evidence of substituting into \(n(A \cup B) = n(A) + n(B) – n(A \cap B)\) (M1)
e.g. \(75 + 55 – 100\) , Venn diagram
30 A1 N2
(ii) 45 A1 N1
[3 marks]
(i) METHOD 1
evidence of using complement, Venn diagram (M1)
e.g. \(1 – p\) , \(100 – 30\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
METHOD 2
attempt to find P(only one sport) , Venn diagram (M1)
e.g. \(\frac{{25}}{{100}} + \frac{{45}}{{100}}\)
\(\frac{{70}}{{100}}\) \(\left( { = \frac{7}{{10}}} \right)\) A1 N2
(ii) \(\frac{{45}}{{70}}\) \(\left( { = \frac{9}{{14}}} \right)\) A2 N2
[4 marks]
valid reason in words or symbols (R1)
e.g. \({\rm{P}}(A \cap B) = 0\) if mutually exclusive, \({\rm{P}}(A \cap B) \ne 0\) if not mutually exclusive
correct statement in words or symbols A1 N2
e.g. \({\rm{P}}(A \cap B) = 0.3\) , \({\rm{P}}(A \cup B) \ne {\rm{P}}(A) + {\rm{P}}(B)\) , \({\rm{P}}(A) + {\rm{P}}(B) > 1\) , some students play both sports, sets intersect
[2 marks]
valid reason for independence (R1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B)\) , \({\rm{P}}(B|A) = {\rm{P}}(B)\)
correct substitution A1A1 N3
e.g. \(\frac{{30}}{{100}} \ne \frac{{75}}{{100}} \times \frac{{55}}{{100}}\) , \(\frac{{30}}{{55}} \ne \frac{{75}}{{100}}\)
[3 marks]