Question
A bakery makes two types of muffins: chocolate muffins and banana muffins.
The weights, C grams, of the chocolate muffins are normally distributed with a mean of 62g and standard deviation of 2.9g.
(a) Find the probability that a randomly selected chocolate muffin weighs less than 61g.
(b) In a random selection of 12 chocolate muffins, find the probability that exactly 5 weigh less than 61g.
The weights, B grams, of the banana muffins are normally distributed with a mean of 68 g and standard deviation of 3.4g.
Each day 60% of the muffins made are chocolate.
On a particular day, a muffin is randomly selected from all those made at the bakery.
(c) (i) Find the probability that the randomly selected muffin weighs less than 61 g .
(ii) Given that a randomly selected muffin weighs less than 61g, find the probability that it is chocolate.
The machine that makes the chocolate muffins is adjusted so that the mean weight of the chocolate muffins remains the same but their standard deviation changes to σ g. The machine that makes the banana muffins is not adjusted. The probability that the weight of a randomly selected muffin from these machines is less than 61g is now 0.157.
(d) Find the value of σ .
Answer/Explanation
Ans:
(a) P(C< 61)
= 0.365112…
= 0.365
(b) recognition of binomial eg X ˜ B(12,0.365…)
P( x = 5) = 0.213666…
= 0.214
(c) (i) Let CM represent ‘chocolate muffin’ and BM represent ‘banana muffin’
P(B<61) = 0.0197555…
EITHER
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) (or equivalent in words)
OR
tree diagram showing two ways to have a muffin weigh < 61
THEN
(0.6 × 0.365…) + (0.4 × 0.0197…)
= 0.226969…
= 0.227
(ii) recognizing conditional probability
Note: Recognition must be shown in context either in words or symbols, not just P (A|B) .
\(\frac{0.6\times 0.365112…}{0.22699…}\)
= 0.965183…
= 0.965
(d) METHOD 1
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) = 0.157
(0.6 × P(C<61))+ (0.4 × 0.0197555….) = 0.157
P(C<61) = 0.248496….
attempt to solve for σ using GDC
Note: Award (M1) for a graph or table of values to show their P (C<61) with a variable standard deviation.
σ =1.47225…
σ = 1.47 (g)
METHOD 2
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) = 0.157
(0.6 × P(C<61))+ (0.4 × 0.0197555….) = 0.157
P(C<61) = 0.248496….
use of inverse normal to find z score of their P(C< 61)
z = −0.679229…
correct substitution
\(\frac{61-62}{\sigma }\) = -0.679229…
σ =1.47225…
σ = 1.47 (g)
Question
A company produces a large number of water containers. Each container has two parts, a bottle and a cap. The bottles and caps are tested to check that they are not defective.
A cap has a probability of 0.012 of being defective. A random sample of 10 caps is selected for inspection.
Find the probability that exactly one cap in the sample will be defective.
The sample of caps passes inspection if at most one cap is defective. Find the probability that the sample passes inspection.
The heights of the bottles are normally distributed with a mean of \(22{\text{ cm}}\) and a standard deviation of \(0.3{\text{ cm}}\).
(i) Copy and complete the following diagram, shading the region representing where the heights are less than \(22.63{\text{ cm}}\).
(ii) Find the probability that the height of a bottle is less than \(22.63{\text{ cm}}\).
(i) A bottle is accepted if its height lies between \(21.37{\text{ cm}}\) and \(22.63{\text{ cm}}\). Find the probability that a bottle selected at random is accepted.
(ii) A sample of 10 bottles passes inspection if all of the bottles in the sample are accepted. Find the probability that the sample passes inspection.
The bottles and caps are manufactured separately. A sample of 10 bottles and a sample of 10 caps are randomly selected for testing. Find the probability that both samples pass inspection.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on whether candidates use tables or GDCs, or their 3 sf answers in subsequent parts. Do not penalise answers that are consistent with their working and check carefully for FT.
evidence of recognizing binomial (seen anywhere in the question) (M1)
e.g. \(_n{C_r}{p^r}{q^{n – r}}\) , \({\text{B}}(n{\text{, }}p)\) , \(^{10}{C_1}{(0.012)^1}{(0.988)^9}\)
\(p = 0.108\) A1 N2
[2 marks]
valid approach (M1)
e.g. \({\rm{P}}(X \le 1)\) , \(0.88627 \ldots + 0.10764 \ldots \)
\(p = 0.994\) A1 N2
[2 marks]
(i)
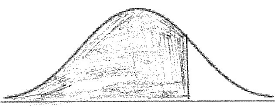A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to left of their vertical line.
(ii) valid approach (M1)
e.g. \({\rm{P}}(X < 22.63)\)
working to find standardized value (A1)
e.g. \(\frac{{22.63 – 22}}{{0.3}}\) , 2.1
\(p = 0.982\) A1 N3
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(21.37 < X < 22.63)\) , \({\rm{P}}( – 2.1 < z < 2.1)\)
correct working (A1)
e.g. \(0.982 – (1 – 0.982)\)
\(p = 0.964\) A1 N3
(ii) correct working (A1)
e.g. \(X \sim {\rm{B}}(10,0.964)\) , \({(0.964)^{10}}\)
\(p = 0.695\) (accept 0.694 from tables) A1 N2
[5 marks]
valid approach (M1)
e.g. \({\rm{P}}(A \cap B) = {\rm{P}}(A){\rm{P}}(B)\) , \((0.994) \times {(0.964)^{10}}\)
\(p = 0.691\) (accept \(0.690\) from tables) A1 N2
[2 marks]
Question
A factory has two machines, A and B. The number of breakdowns of each machine is independent from day to day.
Let \(A\) be the number of breakdowns of Machine A on any given day. The probability distribution for \(A\) can be modelled by the following table.
Let \(B\) be the number of breakdowns of Machine B on any given day. The probability distribution for \(B\) can be modelled by the following table.
On Tuesday, the factory uses both Machine A and Machine B. The variables \(A\) and \(B\) are independent.
Find \(k\).
(i) A day is chosen at random. Write down the probability that Machine A has no breakdowns.
(ii) Five days are chosen at random. Find the probability that Machine A has no breakdowns on exactly four of these days.
Find \({\text{E}}(B)\).
(i) Find the probability that there are exactly two breakdowns on Tuesday.
(ii) Given that there are exactly two breakdowns on Tuesday, find the probability that both breakdowns are of Machine A.
Answer/Explanation
Markscheme
evidence of summing to 1 (M1)
eg\(\,\,\,\,\,\)\(0.55 + 0.3 + 0.1 + k = 1\)
\(k = 0.05{\text{ (exact)}}\) A1 N2
[2 marks]
(i) 0.55 A1 N1
(ii) recognizing binomial probability (M1)
eg\(\,\,\,\,\,\)\(X:{\text{ }}B(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} 5 \\ 4 \end{array}} \right),{\text{ }}{(0.55)^4}(1 – 0.55),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{q^{n – r}}\)
\(P(X = 4) = 0.205889\)
\(P(X = 4) = 0.206\) A1 N2
[3 marks]
correct substitution into formula for \({\text{E}}(X)\) (A1)
eg\(\,\,\,\,\,\)\(0.2 + (2 \times 0.08) + (3 \times 0.02)\)
\({\text{E}}(B) = 0.42{\text{ (exact)}}\) A1 N2
[2 marks]
(i) valid attempt to find one possible way of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)\(2A,{\text{ }}2B,{\text{ }}1A\) and \(1B\), tree diagram
one correct calculation for 1 way (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(0.1 \times 0.7,{\text{ }}0.55 \times 0.08,{\text{ }}0.3 \times 0.2\)
recognizing there are 3 ways of having 2 breakdowns (M1)
eg\(\,\,\,\,\,\)A twice or B twice or one breakdown each
correct working (A1)
eg\(\,\,\,\,\,\)\((0.1 \times 0.7) + (0.55 \times 0.08) + (0.3 \times 0.2)\)
\({\text{P(2 breakdowns)}} = 0.174{\text{ (exact)}}\) A1 N3
(ii) recognizing conditional probability (M1)
eg\(\,\,\,\,\,\)\({\text{P}}(A|B),{\text{ P}}(2A|{\text{2breakdowns}})\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\frac{{0.1 \times 0.7}}{{0.174}}\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402298\)
\({\text{P}}(A = 2|{\text{two breakdowns}}) = 0.402\) A1 N2
[8 marks]