Question
A particle P moves along a straight line. Its velocity \({v_{\text{P}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{P}}} = \sqrt t \sin \left( {\frac{\pi }{2}t} \right)\), for \(0 \leqslant t \leqslant 8\). The following diagram shows the graph of \({v_{\text{P}}}\).
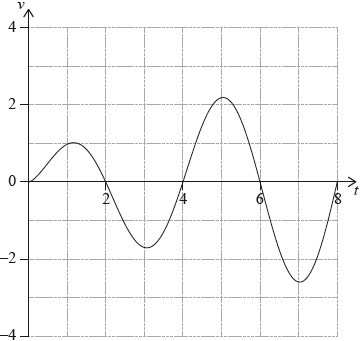
Write down the first value of \(t\) at which P changes direction.
Find the total distance travelled by P, for \(0 \leqslant t \leqslant 8\).
A second particle Q also moves along a straight line. Its velocity, \({v_{\text{Q}}}{\text{ m}}\,{{\text{s}}^{ – 1}}\) after \(t\) seconds is given by \({v_{\text{Q}}} = \sqrt t \) for \(0 \leqslant t \leqslant 8\). After \(k\) seconds Q has travelled the same total distance as P.
Find \(k\).
Answer/Explanation
Markscheme
\(t = 2\) A1 N1
[1 mark]
substitution of limits or function into formula or correct sum (A1)
eg\(\,\,\,\,\,\)\(\int_0^8 {\left| v \right|{\text{d}}t,{\text{ }}\int {\left| {{v_Q}} \right|{\text{d}}t,{\text{ }}\int_0^2 {v{\text{d}}t – \int_2^4 {v{\text{d}}t + \int_4^6 {v{\text{d}}t – \int_6^8 {v{\text{d}}t} } } } } } \)
9.64782
distance \( = 9.65{\text{ (metres)}}\) A1 N2
[2 marks]
correct approach (A1)
eg\(\,\,\,\,\,\)\(s = \int {\sqrt t ,{\text{ }}\int_0^k {\sqrt t } } {\text{d}}t,{\text{ }}\int_0^k {\left| {{v_{\text{Q}}}} \right|{\text{d}}t} \)
correct integration (A1)
eg\(\,\,\,\,\,\)\(\int {\sqrt t = \frac{2}{3}{t^{\frac{3}{2}}} + c,{\text{ }}\left[ {\frac{2}{3}{x^{\frac{3}{2}}}} \right]_0^k,{\text{ }}\frac{2}{3}{k^{\frac{3}{2}}}} \)
equating their expression to the distance travelled by their P (M1)
eg\(\,\,\,\,\,\)\(\frac{2}{3}{k^{\frac{3}{2}}} = 9.65,{\text{ }}\int_0^k {\sqrt t {\text{d}}t = 9.65} \)
5.93855
5.94 (seconds) A1 N3
[4 marks]
