Question
Consider the curve \(y = \sqrt{x}\).
(a) (i) Find \(\frac{dy}{dx}\).
(ii) Hence show that the equation of the tangent to the curve at the point (0.16, 0.4) is y = 1.25x + 0.2.
The shape of a piece of metal can be modelled by the region bounded by the functions f , g,
the x-axis and the line segment [AB], as shown in the following diagram. The units on the x
and y axes are measured in metres.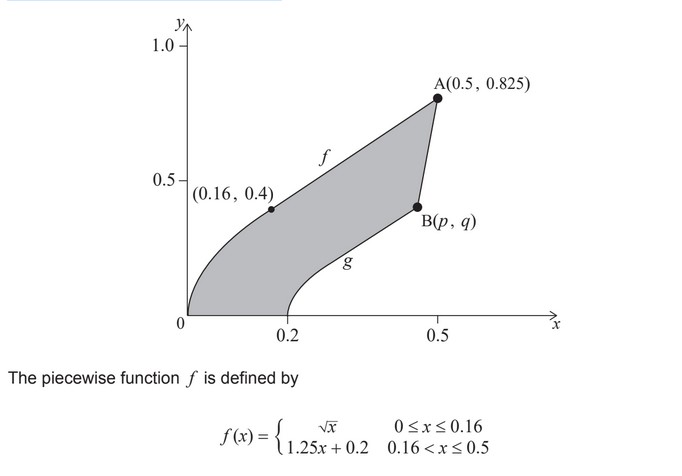
The graph of g is obtained from the graph of f by:
- a sketch scale factor of \(\frac{1}{2}\) in the x direction,
- followed by a stretch scale factor \(\frac{1}{2}\) in the y direction,
- followed by a translation of 0.2 units to the right.
Point A lies on the graph of f and has coordinates (0.5, 0.825). Point B is the image of A
under the given transformations and has coordinates (p , q).
(b) Find the value of p and the value of q.
The piecewise function g is given by
\(g(x)=\left\{\begin{matrix}
h(x) & 0.2 \leq x \leq a\\
1.25x + b & a<x \leq p
\end{matrix}\right.\)
(c) Find
(i) an expression for h(x).
(ii) the value of a.
(iii) the value of b.
(d) (i) Find the area enclosed by y = f (x), the x-axis and the line x = 0.5.
The area enclosed by y = g(x), the x-axis and the line x = p is 0.0627292 \(m^2\) correct to six significant figures.
(ii) Find the area of the shaded region on the diagram.
▶️Answer/Explanation
Ans:
(a) (i) \(y=x^{\frac{1}{2}}\)
\(\frac{dy}{dx}=\frac{1}{2} x^{-\frac{1}{2}}\)
(ii) gradient at x = 0.16 is \(\frac{1}{2} \times \frac{1}{\sqrt{0.16}}\)
= 1.25
EITHER
y – 0.4 = 1.25 (x – 0.16)
OR
0.4 = 1.25(0.16) + b
THEN
hence y = 1.25x + 0.2
(b) p q = = 0.45, 0.4125 ( 0.413) or (accept “(0.45, 0.4125)”)
(c) (i) \((h(x)=) \frac{1}{2} \sqrt{2(x-0.2)}\)
(ii) (a=) 0.28
(iii) EITHER
correct substitution of their part (b) (or (0.28, 0.2)) into the given expression
OR
\(\frac{1}{2}(1.25 \times 2 (x – 0.2)+0.2)\)
THEN
(b=) – 0.15
(d) (i) recognizing need to add two integrals
\(\int_{0}^{0.16} \sqrt{x}dx + \int_{0.16}^{0.5}(1.25x + 0.2)dx\)
0.251 \(m^2\) (0.250916…)
(ii) EITHER
area of trapezoid \(\frac{1}{2} \times 0.05(0.4125 + 0.825) = 0.0309375\)
OR
\(\int_{0.45}^{0.5}(8.25x – 3.3)dx = 0.0309375\)
THEN
shaded area = 0.250916… – 0.627292 – 0.0309375
= 0.157 \(m^2\) (0.15725)
Question
The transformations T1, T2, T3, T4, in the plane are defined as follows:
T1 : A rotation of 360° about the origin
T2 : An anticlockwise rotation of 270° about the origin
T3 : A rotation of 180° about the origin
T4 : An anticlockwise rotation of 90° about the origin.
The transformation T5 is defined as a reflection in the \(x\)-axis.
The transformation T is defined as the composition of T3 followed by T5 followed by T4.
a.Copy and complete the following Cayley table for the transformations of T1, T2, T3, T4, under the operation of composition of transformations.
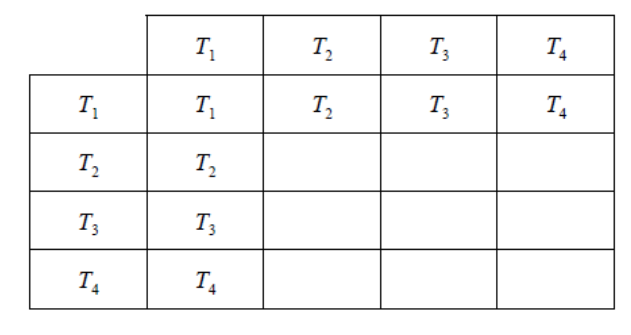 [2]
[2]
b.i.Show that T1, T2, T3, T4 under the operation of composition of transformations form a group. Associativity may be assumed.[3]
b.ii.Show that this group is cyclic.[1]
c.Write down the 2 × 2 matrices representing T3, T4 and T5.[3]
d.i.Find the 2 × 2 matrix representing T.[2]
d.ii.Give a geometric description of the transformation T.[1]
▶️Answer/Explanation
Markscheme
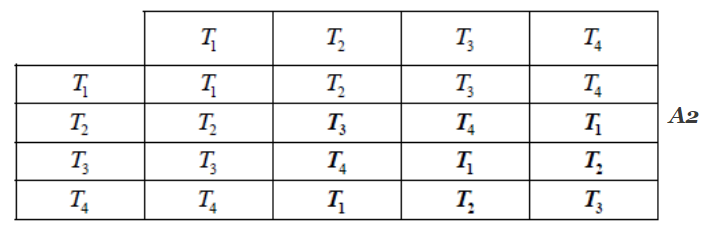
[2 marks]
Note: Award A1 for 6, 7 or 8 correct.
the table is closed – no new elements A1
T1 is the identity A1
T3 (and T1) are self-inverse; T2 and T4 are an inverse pair. Hence every element has an inverse A1
hence it is a group AG
[3 marks]
all elements in the group can be generated by T2 (or T4) R1
hence the group is cyclic AG
[1 mark]
T3 is represented by \(\left( {\begin{array}{*{20}{c}}
{ – 1}&0 \\
0&{ – 1}
\end{array}} \right)\) A1
T4 is represented by \(\left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
1&0
\end{array}} \right)\) A1
T5 is represented by \(\left( {\begin{array}{*{20}{c}}
1&0 \\
0&{ – 1}
\end{array}} \right)\) A1
[3 marks]
\(\left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
1&0
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&0 \\
0&{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{ – 1}&0 \\
0&{ – 1}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
{ – 1}&0
\end{array}} \right)\) (M1)A1
Note: Award M1A0 for multiplying the matrices in the wrong order.
[2 marks]
a reflection in the line \(y = – x\) A1
[1 mark]
Question
The hyperbola with equation \({x^2} – 4xy – 2{y^2} = 3\) is rotated through an acute anticlockwise angle \(\alpha \) about the origin.
a.The point \((x,{\text{ }}y)\) is rotated through an anticlockwise angle \(\alpha \) about the origin to become the point \((X,{\text{ }}Y)\). Assume that the rotation can be represented by
\[\left[ {\begin{array}{*{20}{c}} X \\ Y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right].\]
Show, by considering the images of the points \((1,{\text{ }}0)\) and \((0,{\text{ }}1)\) under this rotation that
\[\left[ {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos \alpha }&{ – \sin \alpha } \\ {\sin \alpha }&{\cos \alpha } \end{array}} \right].\][3]
b.i.By expressing \((x,{\text{ }}y)\) in terms of \((X,{\text{ }}Y)\), determine the equation of the rotated hyperbola in terms of \(X\) and \(Y\).[3]
b.ii.Verify that the coefficient of \(XY\) in the equation is zero when \(\tan \alpha = \frac{1}{2}\).[3]
b.iii.Determine the equation of the rotated hyperbola in this case, giving your answer in the form \(\frac{{{X^2}}}{{{A^2}}} – \frac{{{Y^2}}}{{{B^2}}} = 1\).[3]
b.iv.Hence find the coordinates of the foci of the hyperbola prior to rotation.[5]
▶️Answer/Explanation
Markscheme
consider \(\left[ {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} a \\ c \end{array}} \right]\) (M1)
the image of \((1,{\text{ }}0)\) is \((\cos \alpha ,{\text{ }}\sin \alpha )\) A1
therefore \(a = \cos \alpha ,{\text{ }}c = \sin \alpha \) AG
consider \(\left[ {\begin{array}{*{20}{c}} a&b \\ c&d \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} b \\ d \end{array}} \right]\)
the image of \((0,{\text{ }}1)\) is \(( – \sin \alpha ,{\text{ }}\cos \alpha )\) A1
therefore \(b = – \sin \alpha ,{\text{ }}d = \cos \alpha \) AG
[3 marks]
\(\left[ {\begin{array}{*{20}{c}} X \\ Y \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos \alpha }&{ – \sin \alpha } \\ {\sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \end{array}} \right] \Rightarrow \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha } \\ { – \sin \alpha }&{\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X \\ Y \end{array}} \right]\)
or \(x = X\cos \alpha + Y\sin \alpha ,{\text{ }}y = – X\sin \alpha + Y\cos \alpha \) A1
substituting in the equation of the hyperbola, M1
\({(X\cos \alpha + Y\sin \alpha )^2} – 4(X\cos \alpha + Y\sin \alpha )( – X\sin \alpha + Y\cos \alpha )\)
\( – 2{( – X\sin \alpha + Y\cos \alpha )^2} = 3\) A1
\({X^2}({\cos ^2}\alpha – 2{\sin ^2}\alpha + 4\sin \alpha \cos \alpha ) + \)
\(XY(2\sin \alpha \cos \alpha – 4{\cos ^2}\alpha + 4{\sin ^2}\alpha + 4\sin \alpha \cos \alpha ) + \)
\({Y^2}({\sin ^2}\alpha – 2{\cos ^2}\alpha – 4\sin \alpha \cos \alpha ) = 3\)
[??? marks]
when \(\tan \alpha = \frac{1}{2},{\text{ }}\sin \alpha = \frac{1}{{\sqrt 5 }}\) and \(\cos \alpha = \frac{2}{{\sqrt 5 }}\) A1
the \(XY{\text{ term}} = 6\sin \alpha \cos \alpha – 4{\cos ^2}\alpha + 4{\sin ^2}\alpha \) M1
\( = 6 \times \frac{1}{{\sqrt 5 }} \times \frac{2}{{\sqrt 5 }} – 4 \times \frac{4}{5} + 4 \times \frac{1}{5}\left( {\frac{{12}}{5} – \frac{{16}}{5} + \frac{4}{5}} \right)\) A1
\( = 0\) AG
[??? marks]
the equation of the rotated hyperbola is
\(2{X^2} – 3{Y^2} = 3\) M1A1
\(\frac{{{X^2}}}{{{{\left( {\sqrt {\frac{3}{2}} } \right)}^2}}} – \frac{{{Y^2}}}{{{{(1)}^2}}} = 1\) A1
\(\left( {{\text{accept }}\frac{{{X^2}}}{{\frac{3}{2}}} – \frac{{{Y^2}}}{1} = 1} \right)\)
[??? marks]
the coordinates of the foci of the rotated hyperbola
are \(\left( { \pm \sqrt {\frac{3}{2} + 1} ,{\text{ }}0} \right) = \left( { \pm \sqrt {\frac{5}{2}} ,{\text{ }}0} \right)\) M1A1
the coordinates of the foci prior to rotation were given by
\(\left[ {\begin{array}{*{20}{c}} {\frac{2}{{\sqrt 5 }}}&{\frac{1}{{\sqrt 5 }}} \\ { – \frac{1}{{\sqrt 5 }}}&{\frac{2}{{\sqrt 5 }}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { \pm \sqrt {\frac{5}{2}} } \\ 0 \end{array}} \right]\)
M1A1
\(\left[ {\begin{array}{*{20}{c}} { \pm \sqrt 2 } \\ { \mp \frac{1}{{\sqrt 2 }}} \end{array}} \right]\) A1
[??? marks]
Question
a.By considering the points \((1,{\text{ }}0)\) and \((0,{\text{ }}1)\) determine the \(2 \times 2\) matrix which represents
(i) an anticlockwise rotation of \(\theta \) about the origin;
(ii) a reflection in the line \(y = (\tan \theta )x\).[5]
b.Determine the matrix \(A\) which represents a rotation from the direction \(\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)\) to the direction \(\left( {\begin{array}{*{20}{c}} 1 \\ 3 \end{array}} \right)\).[2]
c.A triangle whose vertices have coordinates \((0,{\text{ }}0)\), \((3,{\text{ }}1)\) and \((1,{\text{ }}5)\) undergoes a transformation represented by the matrix \({A^{ – 1}}XA\), where \(X\) is the matrix representing a reflection in the \(x\)-axis. Find the coordinates of the vertices of the transformed triangle.[6]
d.The matrix \(B = {A^{ – 1}}XA\) represents a reflection in the line \(y = mx\). Find the value of \(m\).[6]
▶️Answer/Explanation
Markscheme
(i) under an anti-clockwise rotation of \(\theta \)
\((1,{\text{ }}0) \to (\cos \theta ,{\text{ }}\sin \theta )\)
\((0,{\text{ }}1) \to ( – \sin \theta ,{\text{ }}\cos \theta )\) M1
rotation matrix is \(\left( {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta } \\ {\sin \theta }&{\cos \theta } \end{array}} \right)\) A1
(ii) 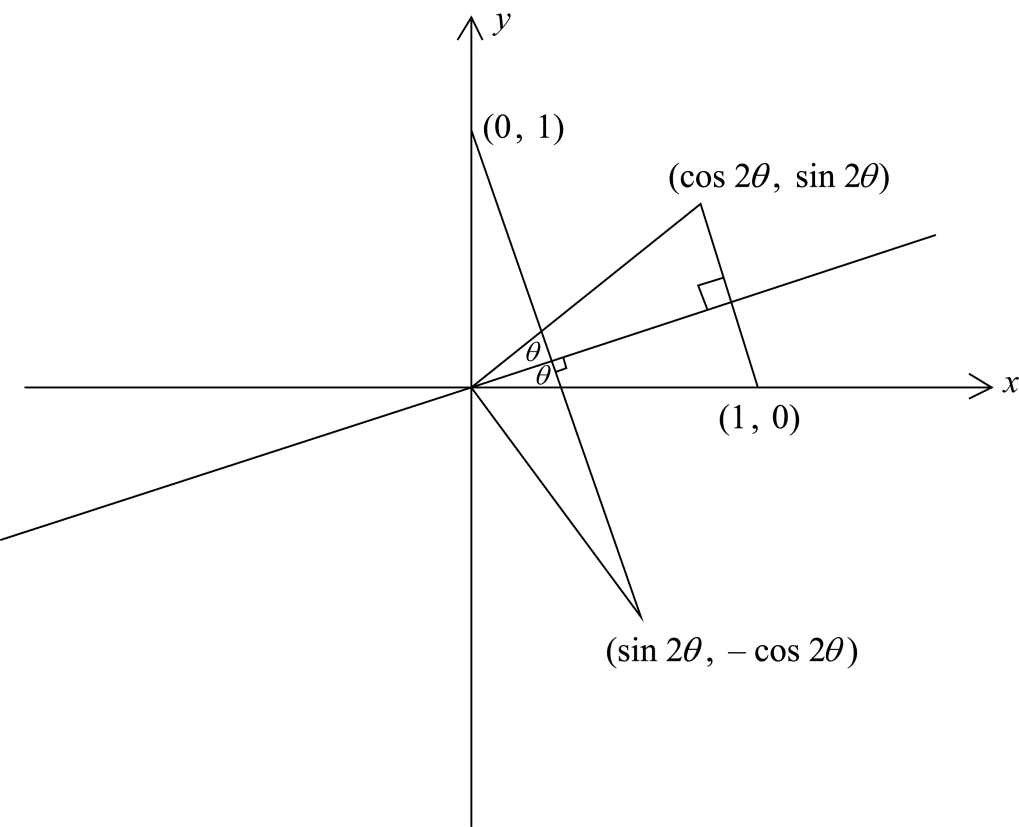 M1
M1
under a reflection in the line \(y = (\tan \theta )x\)
\((1,{\text{ }}0) \to (\cos 2\theta ,{\text{ }}\sin 2\theta )\)
\((0,{\text{ }}1) \to (\sin 2\theta ,{\text{ }} – \cos 2\theta )\) M1
matrix for reflection in the line \(y = (\tan \theta )x: \left( {\begin{array}{*{20}{c}} {\cos 2\theta }&{\sin 2\theta } \\ {\sin 2\theta }&{ – \cos 2\theta } \end{array}} \right)\) A1
in this case \(\tan \theta = 3\) (M1)
\(\Rightarrow \sin \theta = \frac{3}{{\sqrt {10} }}\)
hence rotation matrix is \(\left( {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt {10} }}}&{ – \frac{3}{{\sqrt {10} }}} \\ {\frac{3}{{\sqrt {10} }}}&{\frac{1}{{\sqrt {10} }}} \end{array}} \right)\) A1
\({A^{ – 1}} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt {10} }}}&{\frac{3}{{\sqrt {10} }}} \\ { – \frac{3}{{\sqrt {10} }}}&{\frac{1}{{\sqrt {10} }}} \end{array}} \right)\) (A1)
\(X = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ – 1} \end{array}} \right)\) (A1)
\( \Rightarrow {A^{ – 1}}XA = \left( {\begin{array}{*{20}{c}} { – \frac{8}{{10}}}&{ – \frac{6}{{10}}} \\ { – \frac{6}{{10}}}&{\frac{8}{{10}}} \end{array}} \right)\) (M1)A1
\( \Rightarrow {A^{ – 1}}XA(G) = \left( {\begin{array}{*{20}{c}} { – \frac{8}{{10}}}&{ – \frac{6}{{10}}} \\ { – \frac{6}{{10}}}&{\frac{8}{{10}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0&3&1 \\ 0&1&5 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0&{ – 3}&{ – \frac{{19}}{5}} \\ 0&{ – 1}&{\frac{{17}}{5}} \end{array}} \right)\) (M1)
hence coordinates are \((0,{\text{ }}0)\), \(( – 3,{\text{ }} – 1)\) and \(\left( { – \frac{{19}}{5},{\text{ }}\frac{{17}}{5}} \right)\) A1
\(B = \left( {\begin{array}{*{20}{c}} { – \frac{8}{{10}}}&{ – \frac{6}{{10}}} \\ { – \frac{6}{{10}}}&{\frac{8}{{10}}} \end{array}} \right)\)
the matrix for the reflection in the line \(y = (\tan \theta )x\) is \(\left( {\begin{array}{*{20}{c}} {\cos 2\theta }&{\sin 2\theta } \\ {\sin 2\theta }&{ – \cos 2\theta } \end{array}} \right)\)
\(\cos 2\theta = – \frac{4}{5},{\text{ }}\sin 2\theta = – \frac{3}{5}\) (A1)(A1)
\(\cos 2\theta = 2{\cos ^2}\theta – 1\) (M1)
\( \Rightarrow 2{\cos ^2}\theta = \frac{2}{{10}}\)
\( \Rightarrow \cos \theta = \pm \frac{1}{{\sqrt {10} }}\) (A1)
\( \Rightarrow \cos \theta = – \frac{1}{{\sqrt {10} }}\) and \(\sin \theta = \frac{3}{{\sqrt {10} }}\) (A1)
\( \Rightarrow \tan \theta = – 3\)
\( \Rightarrow m = – 3\) A1
