Question
Charlie and Daniella each began a fitness programme. On day one, they both ran 500 m. On each subsequent day, Charlie ran 100 m more than the previous day whereas Daniella increased her distance by 2 % of the distance ran on the previous day.
(a) Calculate how far
(i) Charlie ran on day 20 of his fitness programme.
(ii) Daniella ran on day 20 of her fitness programme. [5]
(iii) On day n of the fitness programmes Daniella runs more than Charlie for the first time.
Find the value of n . [3]
▶️Answer/Explanation
(a) (i) attempt to find u20 using an arithmetic sequence e.g. u1 = 500 and d = 100 OR u20= 500+ 1900 OR 500,600,700,… (Charlie ran) 2400 m (ii) (r = ) 1.02 attempt to find u20 using a geometric sequence e.g. identifying u1 = 500 and a value for r OR 500 × r19 OR 500, 510, 520.2,… (Daniella ran) 728 m (728.405…) (b) 500 × 1.02 n-1 > 500 + (n-1) × 100 attempt to solve inequality n >184.215… n =185
Question
Charlie and Daniella each began a fitness programme. On day one, they both ran 500 m. On each subsequent day, Charlie ran 100 m more than the previous day whereas Daniella increased her distance by 2 % of the distance ran on the previous day.
(a) Calculate how far
(i) Charlie ran on day 20 of his fitness programme.
(ii) Daniella ran on day 20 of her fitness programme. [5]
(iii) On day n of the fitness programmes Daniella runs more than Charlie for the first time.
Find the value of n . [3]
▶️Answer/Explanation
(a) (i) attempt to find u20 using an arithmetic sequence e.g. u1 = 500 and d = 100 OR u20= 500+ 1900 OR 500,600,700,… (Charlie ran) 2400 m (ii) (r = ) 1.02 attempt to find u20 using a geometric sequence e.g. identifying u1 = 500 and a value for r OR 500 × r19 OR 500, 510, 520.2,… (Daniella ran) 728 m (728.405…) (b) 500 × 1.02 n-1 > 500 + (n-1) × 100 attempt to solve inequality n >184.215… n =185
Question
5. A ball is dropped from a height of 1.8 metres and bounces on the ground. The maximum
height reached by the ball, after each bounce, is 85% of the previous maximum height.
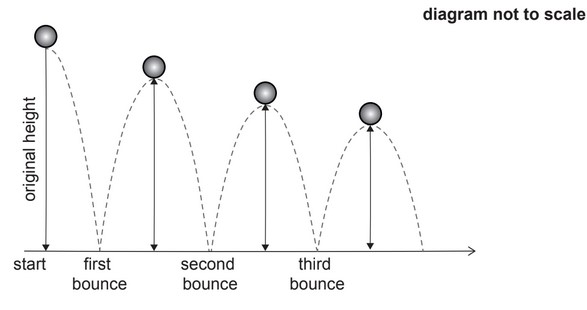
(a) Show that the maximum height reached by the ball after it has bounced for the sixth
time is 68cm, to the nearest cm.
(b) Find the number of times, after the first bounce, that the maximum height reached is
greater than 10cm.
(c) Find the total vertical distance travelled by the ball from the point at which it is dropped
until the fourth bounce.
▶️Answer/Explanation
Ans:
(a) use of geometric sequence with r = 0.85
EITHER
\((0.85)^6(1.8)\) OR 0.678869… OR \((0.85)^5 (1.53)\)
= 0.68m
= 68 cm
OR
\((0.85)^6(180)\) OR \((0.85)^5(153)\)
= 68 cm
(b) EITHER
\((0.85)^n (1.8) > 0.1\) OR \((0.85)^{n-1}(1.53)>0.1\)
17
OR
\((0.85)^{17}(1.8 = 0.114m\) and \((0.85)^{18}(1.8)=0.0966m\)
17
OR
solving \((0.85)^n(1.8)=0.1\) to find n = 17.8
17
(c) EITHER
distance (in one direction) travelled between first and fourth bounce
\(=\frac{(1.8 \times 0.86)(1-0.85^3)}{1-0.85}(=3.935925)\)
recognizing distances are travelled twice except first distance
1.8 + 2 (3.935925)
= 9.67 m (9.67185…m)
OR
distance (in one direction) travelled between drop and fourth bounce
\(=\frac{(1.8)(1-0.85^4)}{1-0.85}(=5.735925)\)
recognizing distances are travelled twice except first distance
2(5.735925)-1.8
= 9.67m (9.67185…m)
OR
distance (in one direction) travelled between first and fourth bounce
\((0.85)(1.8)+(0.85)^2(1.8) (=3.935925…)\)
recognizing distances are travelled twice except first distance
\(1.8+2(0.85)(1.8)+2(0.85)^2(1.8)+2(0.85)^3(1.8)\)
= 9.67m (9.67185…m)
Question
The first term of an arithmetic sequence is \(0\) and the common difference is \(12\).
a.Find the value of the \({96^{{\text{th}}}}\) term of the sequence.[2]
b.The first term of a geometric sequence is \(6\). The \({6^{{\text{th}}}}\) term of the geometric sequence is equal to the \({17^{{\text{th}}}}\) term of the arithmetic sequence given above.
Write down an equation using this information.[2]
c.The first term of a geometric sequence is \(6\). The \\({6^{{\text{th}}}}\) term of the geometric sequence is equal to the \({17^{{\text{th}}}}\) term of the arithmetic sequence given above.
Calculate the common ratio of the geometric sequence.[2]
▶️Answer/Explanation
Markscheme
\({u_{96}} = {u_1} + 95d\) (M1)
\( = 0 + 95 \times 12\)
\( = 1140\) (A1) (C2)
[2 marks]
\(6{r^5} = 16d\) (A1)
\(6{r^5} = 16 \times 12\) (\(192\)) (A1) (C2)
Note: (A1) only, if both terms seen without an equation.[2 marks]
\({r^5} = 32\) (A1)(ft)
Note: (ft) from their (b).
\(r = 2\) (A1)(ft) (C2)[2 marks]
Question
The annual fees paid to a school for the school years 2000, 2001 and 2002 increase as a geometric progression. The table below shows the fee structure.
a.Calculate the common ratio for the increasing sequence of fees.[2]
b.Give your answer correct to 2 decimal places.
The fees continue to increase in the same ratio.
Find the fees paid for 2006.[2]
c.Give your answer correct to 2 decimal places.
The fees continue to increase in the same ratio.
A student attends the school for eight years, starting in 2000.
Find the total fees paid for these eight years.[2]
▶️Answer/Explanation
Markscheme
\(r = \frac{{8320}}{{8000}}\) (or equivalent) (M1)
Note: Award (M1) for dividing correct terms.
r = 1.04 (A1) (C2)
Notes: In (b) and (c) (ft) from candidate’s r.
Allow lists, graphs etc. as working in (b) and (c).[2 marks]
Financial penalty (FP) applies in this part
Fees = 8000 (1.04)6 (M1)
Note: Award (M1) for correct substitution into correct formula.(FP) Fees = 10122.55 USD (USD not required) (A1)(ft) (C2)
Note: Special exception to the note above.
Award maximum of (M1)(A0) if 5 is used as the power.[2 marks]
Financial penalty (FP) applies in this part
\({\text{Total}} = \frac{{8000({{1.04}^8} – 1)}}{{1.04 – 1}}\) (M1)
Notes: Award (M1) for correct substitution into correct formula.
Give full credit for solution by lists.
(FP) Total = 73713.81 USD (USD not required) (A1)(ft) (C2)[2 marks]
Question
The population of big cats in Africa is increasing at a rate of 5 % per year. At the beginning of 2004 the population was \(10\,000\).
a.Write down the population of big cats at the beginning of 2005.[1]
b.Find the population of big cats at the beginning of 2010.[2]
c.Find the number of years, from the beginning of 2004, it will take the population of big cats to exceed \(50\,000\).[3]
▶️Answer/Explanation
Markscheme
\(10\,000 \times 1.05\)
\( = 10\,500\) (A1) (C1)[1 mark]
\(10\,000 \times {1.05^6}\) (M1)
Note: Award (M1) for correct substitution into correct formula.
\( = 13\,400\) (A1) (C2)[2 marks]
\(50\,000 = 10\,000 \times 1.05”\) (M1)(A1)
Note: Award (M1) for \(10\,000 \times 1.05”\) or equivalent, (A1) for \(50\,000\)
\(n = 33.0\) (Accept 33) (A1) (C3)[3 marks]
