Question 10. [Maximum mark: 6]
Tommaso and Pietro have each been given 1500 euro to save for college.
Pietro invests his money in an account that pays a nominal annual interest rate of 2.75 %,
compounded half-yearly.
a. Calculate the amount Pietro will have in his account after 5 years. Give your answer
correct to 2 decimal places. [3]
Tommaso wants to invest his money in an account such that his investment will increase to
1.5 times the initial amount in 5 years. Assume the account pays a nominal annual interest of r % compounded quarterly.
b. Determine the value of r . [3]
Answer/Explanation
(a) METHOD 1
N=5 or N = 10
I%=2.75 or l%= 2.75
PV = -1500 or PV =- 1500
PMY =0 or PMT = 0
P/Y = 2 or P/Y=1
C/Y = 2 or C/Y=2
METHOD 2
\(1500(1+\frac{2.75}{2\times 100})^{2\times 5}1719.49\) euro
(b) METHOD 1

METHOD 2
\(1500(1+\frac{r}{4\times 100})^{4\times 5}= 2250 (1+\frac{r}{4\times 100})^{4\times 5}= 1.5\) r = 8.19 (8.19206…)
Note: Accept r = 8.19% . Accept a trial and error method which leads to r = 8.19 .
Question
A ball is dropped from a height of 1.8 metres and bounces on the ground. The maximum
height reached by the ball, after each bounce, is 85% of the previous maximum height.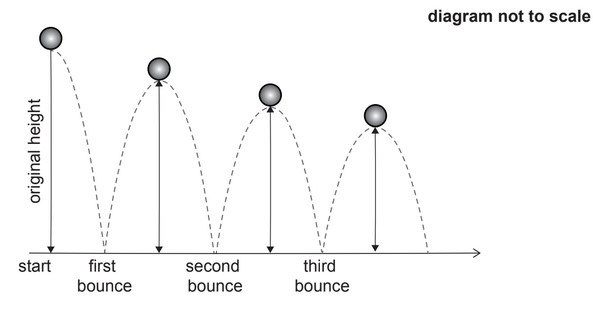
(a) Show that the maximum height reached by the ball after it has bounced for the sixth
time is 68cm, to the nearest cm.
(b) Find the number of times, after the first bounce, that the maximum height reached is
greater than 10cm.
(c) Find the total vertical distance travelled by the ball from the point at which it is dropped
until the fourth bounce.
Answer/Explanation
Ans:
(a) use of geometric sequence with r = 0.85
EITHER
\((0.85)^6(1.8)\) OR 0.678869… OR \((0.85)^5(1.53)\)
= 0.68 m
= 68 cm
OR
\((0.85)^6(180)\) OR \((0.85)^5(153)\)
= 68 cm
(b) EITHER
\((0.85)^n(1.8) > 0.1\) OR \((0.85)^{n-1}(1.53)>0.1\)
17
OR
\((0.85)^{17}(1.8)=0.114m \) and \((0.85)^{18}(1.8)=0.0966 m\)
17
OR
solving \((0.85)^n(1.8)=0.1\) to find n = 17.8
17
(c) EITHER
distance (in one direction) travelled between first and fourth bounce
\(=\frac{(1.8 \times 0.85)(1-0.85^3)}{1-0.85} (=3.935925)\)
recognizing distances are travelled twice except first distance
1.8 + 2(3.935925)
= 9.67 m (9.67185… m)
OR
distance (in one direction) travelled between drop and fourth bounce
\(=\frac{(1.8)(1-0.85^4)}{1-0.85}(=5.735925)\)
recognizing distances are travelled twice except first distance
2(5.735925)-1.8
=9.67m (9.67185…m)
OR
distance (in one direction) travelled between first and fourth bounce
\((0.85)(1.8)+(0.85)^2(1.8)+(0.85)^3(1.8) (=3.935925…)\)
recognizing distances are travelled twice except first distance
\(1.8 + 2(0.85)(1.8)+2(0.85)^2(1.8)+2(0.85)^3(1.8)\)
=9.67 m (9.67185…m)
Question
Ben inherits $6500. Ben invests his money in a bank that pays compound interest at a rate of 4.5% per annum.
Calculate the value of Ben’s investment at the end of 6 years. Give your answer correct to 2 decimal places.
Answer/Explanation
Markscheme
\({\text{Ben Amount}} = 6500{\left( {1 + \frac{{4.5}}{{100}}} \right)^6}\) (M1)(A1)
\( = $8464.69\) (A1)
(M1)(A1)(A0) if interest only found (=$1964.69) (C3)[3 marks]
Question
Charles invests \(3000{\text{ USD}}\) in a bank that offers compound interest at a rate of \(3.5\% \) per annum, compounded half-yearly.
Calculate the number of years that it takes for Charles’s money to double.
Answer/Explanation
Markscheme
\(6000 = 3000{\left( {1 + \frac{{3.5}}{{200}}} \right)^{2n}}\) (M1)(A1)
Note: (M1) for substituting values into a compound interest formula, (A1) for correct values with a variable for the power.
\(n = 20{\text{ years}}\) (A1) (C3)
Note: If \(n\) used in formula instead of \(2n\), can allow as long as final answer is halved to get \(20\).[3 marks]
Question
Emma places \({\text{€}}8000\) in a bank account that pays a nominal interest rate of \(5\% \) per annum, compounded quarterly.
Calculate the amount of money that Emma would have in her account after 15 years. Give your answer correct to the nearest Euro.[3]
After a period of time she decides to withdraw the money from this bank. There is \({\text{€}}9058.17\) in her account. Find the number of months that Emma had left her money in the account.[3]
Answer/Explanation
Markscheme
\(FV = 8000{(1.0125)^{60}}\) (M1)(A1)
Note: (M1) for substituting in compound interest formula, (A1) for correct substitution.
\({\text{€}}16857\) only (A1) (C3)[3 marks]
\(8000{(1.0125)^n} = 9058.17\) (M1)
Note: (M1) for equating compound interest formula to \(9058.17\)
\(n = 10\) correct answer only (A1)
So 30 months, (ft) on their \(n\) (A1)(ft) (C3)
Note: Award (C2) for \(2.5\) seen with no working.[3 marks]