Question
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
a.(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.[3]
b.Calculate \(\sqrt {{{3.87}^5} – {{8.73}^{ – 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .[3]
▶️Answer/Explanation
Markscheme
(i) Mean = (5.96 + 5.95 + 6.02 + 5.95 + 5.99) / 5 = 5.974 (5.97) (A1)
(ii) \({\text{% error}} = \frac{{error}}{{actualvalue}} \times 100\% \)
\( = \frac{{6 – 5.974}}{{5.974}} \times 100\% = 0.435\% \) (M1)(A1)(ft)
(M1) for correctly substituted formula.
Allow 0.503% as follow through from 5.97
Note: An answer of 0.433% is incorrect. (C3)
[3 marks]
number is 29.45728613
(i) Nearest integer = 29 (A1)
(ii) Standard form = 2.95 × 101 (accept 2.9 × 101) (A1)(ft)(A1)
Award (A1) for each correct term
Award (A1)(A0) for 2.95 × 10 (C3)
[3 marks]
Question
a.Write down the following numbers in increasing order.
\(3.5\), \(1.6 \times 10^{−19}\), \(60730\), \(6.073 \times 10^{5}\), \(0.006073 \times 10^6\), \(\pi\), \(9.8 \times 10^{−18}\).[3]
b.Write down the median of the numbers in part (a).[1]
c.State which of the numbers in part (a) is irrational.[1]
▶️Answer/Explanation
Markscheme
\(1.6 \times 10^{−19}\), \(9.8 \times 10^{−18}\), \(\pi\), \(3.5\), \(0.006073 \times 10^6\), \(60730\), \(6.073 \times 10^{5}\) (A4)
Award (A1) for \(\pi\) before 3.5
Award (A1) for \(1.6 \times 10^{−19}\) before \(9.8 \times 10^{−18}\)
Award (A1) for the three numbers containing 6073 in the correct order.
Award (A1) for the pair with negative indices placed before 3.5 and \(\pi\) and the remaining three numbers placed after (independently of the other three marks).
Award (A3) for numbers given in correct decreasing order.
Award (A2) for decreasing order with at most 1 error (C4)
[3 marks]
The median is 3.5. (A1)(ft)
Follow through from candidate’s list. (C1)
[1 mark]
\(\pi\) is irrational. (A1) (C1)
[1 mark]
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
a.Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.
.
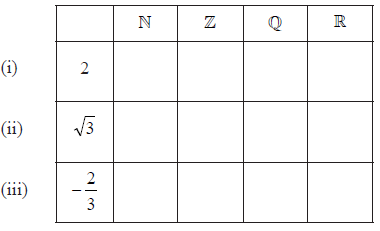[3]
b.A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).[1]
▶️Answer/Explanation
Markscheme
(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.
[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.
[1 mark]
Question
Consider the numbers \(\sqrt 3 \), \(6\), \(2\frac{1}{2}\), \(\pi \), \( – 5\), and the sets \(\mathbb{N}\), \(\mathbb{Z}\), and \(\mathbb{Q}\). Complete the following table by placing a tick in the appropriate box if the number is an element of the set.
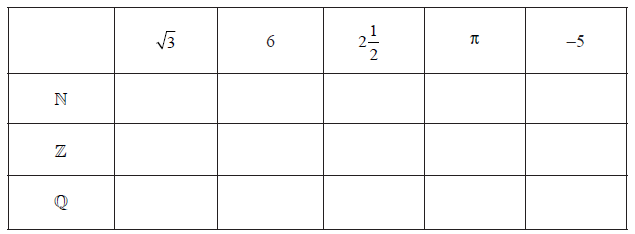
▶️Answer/Explanation
Markscheme
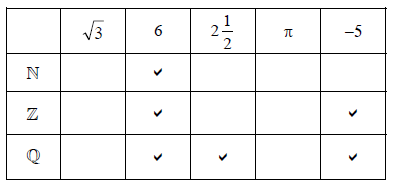
Note: Accept any symbol for ticks. Do not penalize if candidate had also indicated, by a different symbol, that the number is not an element of the set.
Row \(\mathbb{N}\) correct, no extra entries. (A1) (C1)
Row \(\mathbb{Z}\) (A1)(A1) (C2)
Note: Award (A1) for each correct tick and no extra entries. Award (A1) only for both ticks correct and 1 extra entry, (A0) otherwise.
Row \(\mathbb{Q}\) (A1)(A1)(A1) (C3)
Note: Award (A1) for each correct tick and no extra entries. Award (A2) only for all 3 correct and one extra entry. Award (A1) only for 2 correct and one extra entry. (A0) otherwise.
[6 marks]
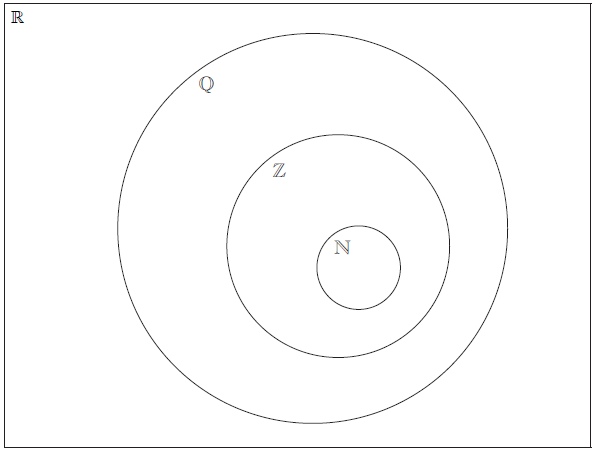
Question
The Venn diagram shows the number sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\). Place each of the following numbers in the appropriate region of the Venn diagram.
\(\frac{{1}}{{4}}\), −3, π, cos 120°, 2.7 × 103, 3.4 × 10–2
▶️Answer/Explanation
Markscheme
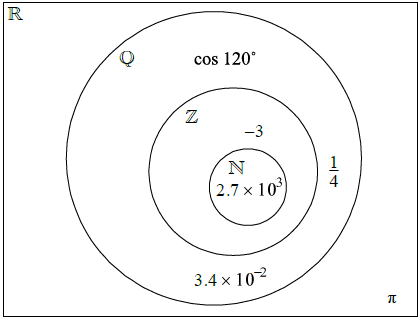(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number placed once in the correct section. Accept equivalent forms for numbers.
[6 marks]