Question
A function is defined by f (x)\( = 2 – \frac{12}{x+5}\) for −7 ≤ x ≤ 7, x ≠ −5.
a. Find the range of f . [3]
b. Find an for the inverse function f −1 (x). The domain is not required. [3]
c. Write down the range of f −1 (x) . [1]
▶️Answer/Explanation
(a) ( f ( −7) =8 ) and ( f (7) 1 = 1) r
ange is f (x ) ≤ 1, f (x ) ≥ 8
(b) interchanging x, y at any stage
\(y= 2 – \frac{12}{x+5}\0
\(\frac{12}{x+5}= 2-y\)
\(\frac{12}{(2-y)}= x+5\)
\frac{12}{(2-y)}- 5=x
\((f^{-1}(x)\frac{12}{2-x}-5)\)
\(= \frac{2+5x}{2-x}\)
(c) range is -7 ≤ f-1 (x) ≤ 7, f-1 (x)≠ 5
Question
1. The height of a baseball after it is hit by a bat is modelled by the function
\(h(t)=-4.8t^2 + 21t + 1.2\)
where h(t) is the height in metres above the ground and t is the time in seconds after the ball was hit.
(a) Write down the height of the ball above the ground at the instant it is hit by the bat.
(b) Find the value of t when the ball hits the ground.
(c) State an appropriate domain for t in this model.
▶️Answer/Explanation
Ans:
(a) 1.2 metres
(b) \(-4.8 t^2 + 21t + 1.2 = 0\)
(t=) 4.43 s (4.431415…s)
(c) \(0 \leq t \leq 4.43\) OR [0, 4.43]
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
a.Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.
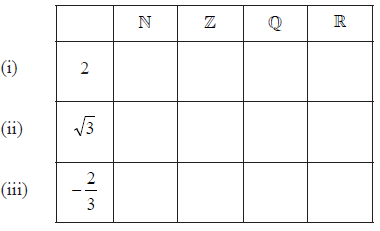[3]
b.A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).[1]
▶️Answer/Explanation
Markscheme
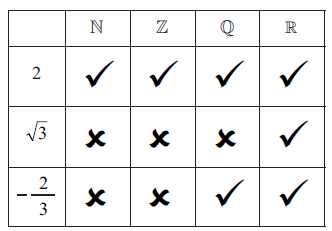(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.[1 mark]
Question
a.Factorise the expression \({x^2} – 3x – 10\).[2]
b.A function is defined as \(f(x) = 1 + {x^3}\) for \(x \in \mathbb{Z}{\text{, }} {- 3} \leqslant x \leqslant 3\).
(i) List the elements of the domain of \(f(x)\).
(ii) Write down the range of \(f(x)\).[4]
▶️Answer/Explanation
Markscheme
\((x – 5)(x + 2)\) (A1)(A1) (C2)
Note: Award (A1) for \((x + 5)(x – 2)\), (A0) otherwise. If equation is equated to zero and solved by factorizing award (A1) for both correct factors, followed by (A0).[2 marks]
(i) \( – 3\), \( – 2\), \( – 1\), \(0\), \(1\), \(2\), \(3\) (A1)(A1) (C2)
Note: Award (A2) for all correct answers seen and no others. Award (A1) for 3 correct answers seen.
(ii) \( – 26\), \( – 7\), 0,1, 2, 9, 28 (A1)(A1) (C2)
Note: Award (A2) for all correct answers seen and no others. Award (A1) for 3 correct answers seen. If domain and range are interchanged award (A0) for (b)(i) and (A1)(ft)(A1)(ft) for (b)(ii).[4 marks]
Question
The graph of a quadratic function \(y = f (x)\) is given below.
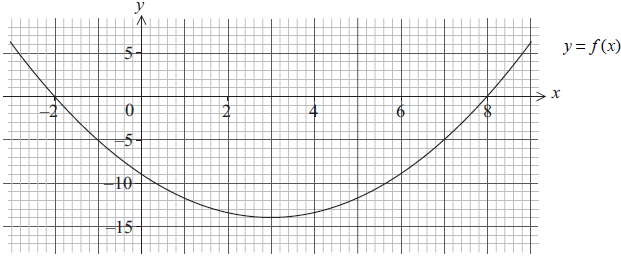
a.Write down the equation of the axis of symmetry.[2]
b.Write down the coordinates of the minimum point.[2]
c.Write down the range of \(f (x)\).[2]
▶️Answer/Explanation
Markscheme
x = 3 (A1)(A1) (C2)
Notes: Award (A1) for “ x = ” (A1) for 3.
The mark for x = is not awarded unless a constant is seen on the other side of the equation.[2 marks]
(3, −14) (Accept x = 3, y = −14) (A1)(ft)(A1) (C2)Note: Award (A1)(A0) for missing coordinate brackets.[2 marks]
y ≥ −14 (A1)(A1)(ft) (C2)
Notes: Award (A1) for y ≥ , (A1)(ft) for –14.
Accept alternative notation for intervals.[2 marks]