Question
The function \(f(x) = 5 – 3({2^{ – x}})\) is defined for \(x \geqslant 0\).
On the axes below sketch the graph of f (x) and show the behaviour of the curve as x increases.[3]
Write down the coordinates of any intercepts with the axes.
[1]
Draw the line y = 5 on your sketch.[1]
Write down the number of solutions to the equation f (x) = 5 .[1]
Answer/Explanation
Markscheme
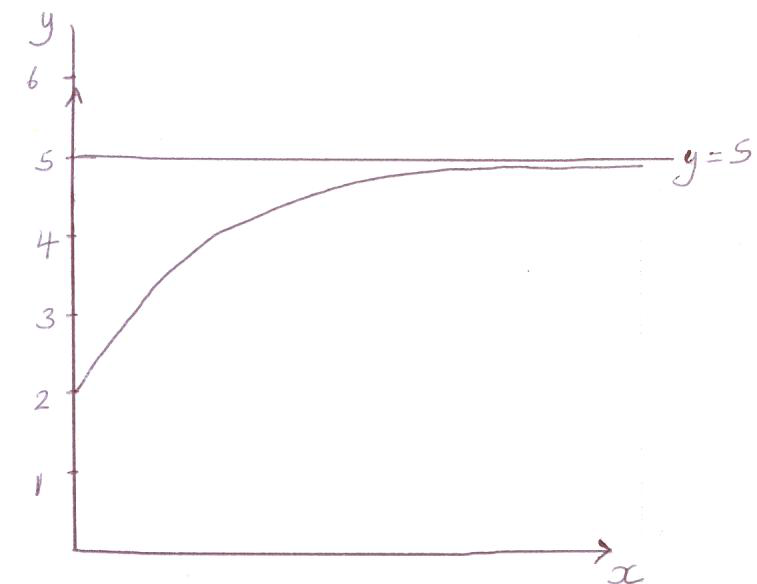(A1)(A1)(A1)
Notes: Award (A1) for labels and scale on y-axis.
Award (A1) for smooth increasing curve in the given domain.
Award (A1) for asymptote implied (\({\text{gradient}} \to {\text{0}}\)).[3 marks]
(0, 2) accept x = 0, y = 2 (A1) (C4)
Note: If incorrect domain used and both (0, 2) and (\( – \)0.737, 0) seen award (A1)(ft).[1 mark]
line passing through (0, 5), parallel to x axis and not intersecting their graph. (A1) (C1)[1 mark]
zero (A1) (C1)[1 mark]
Question
The \(x\)-coordinate of the minimum point of the quadratic function \(f(x) = 2{x^2} + kx + 4\) is \(x =1.25\).
(i) Find the value of \(k\) .
(ii) Calculate the \(y\)-coordinate of this minimum point.[4]
Sketch the graph of \(y = f(x)\) for the domain \( – 1 \leqslant x \leqslant 3\).
[2]
Answer/Explanation
Markscheme
(i) \(1.25 = – \frac{k}{{2(2)}}\) (M1)
OR
\(f'(x) = 4x + k = 0\) (M1)
Note: Award (M1) for setting the gradient function to zero.
\(k = – 5\) (A1) (C2)
(ii) \(2{(1.25)^2} – 5(1.25) + 4\) (M1)
\( = 0.875\) (A1)(ft) (C2)
Note: Follow through from their \(k\).[4 marks]
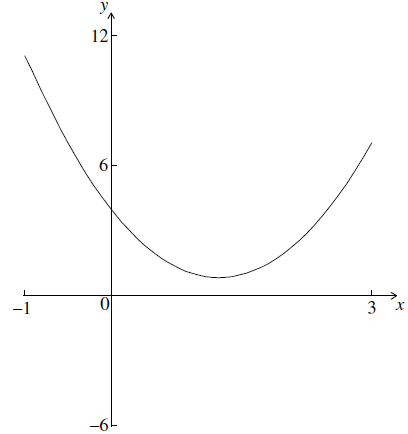(A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for a curve with correct concavity consistent with their \(k\) passing through (0, 4).
(A1)(ft) for minimum in approximately the correct place. Follow through from their part (a).[2 marks]
Question
y = f (x) is a quadratic function. The graph of f (x) intersects the y-axis at the point A(0, 6) and the x-axis at the point B(1, 0). The vertex of the graph is at the point C(2, –2).
Write down the equation of the axis of symmetry.[2]
Sketch the graph of y = f (x) on the axes below for 0 ≤ x ≤ 4 . Mark clearly on the sketch the points A , B , and C.
[3]
The graph of y = f (x) intersects the x-axis for a second time at point D.
Write down the x-coordinate of point D.[1]
Answer/Explanation
Markscheme
x = 2 (A1)(A1) (C2)
Notes: Award (A1)(A0) for “ x = constant” (other than 2). Award (A0)(A1) for y = 2. Award (A0)(A0) for only seeing 2. Award (A0)(A0) for 2 = –b / 2a.[2 marks]
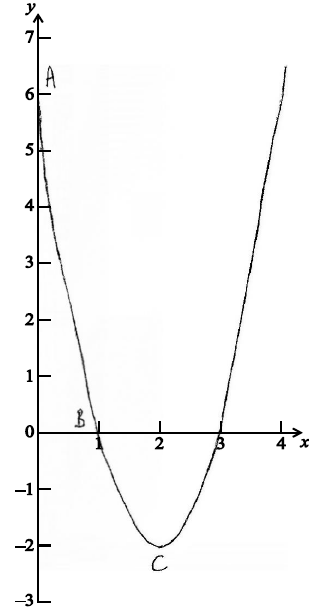
(A1) for correctly plotting and labelling A, B and C
(A1) for a smooth curve passing through the three given points
(A1) for completing the symmetry of the curve over the domain given. (A3) (C3)
Notes: For A marks to be awarded for the curve, each segment must be a reasonable attempt at a continuous curve. If straight line segments are used, penalise once only in the last two marks.[3 marks]
3 (A1)(ft) (C1)
Notes: (A0) for coordinates. Accept x = 3 or D = 3 .[1 mark]
Question
Consider the two functions, \(f\) and \(g\), where
\(f(x) = \frac{5}{{{x^2} + 1}}\)
\(g(x) = {(x – 2)^2}\)
Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the axes below. Indicate clearly the points where each graph intersects the y-axis.
[4]Use your graphic display calculator to solve \(f(x) = g(x)\).[2]
Answer/Explanation
Markscheme
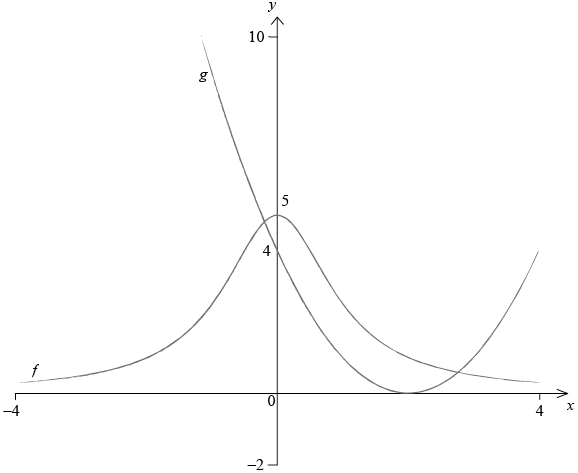
\(f(x)\): a smooth curve symmetrical about y-axis, \(f(x) > 0\) (A1)
Note: If the graph crosses the x-axis award (A0).
Intercept at their numbered \(y = 5\) (A1)
Note: Accept clear scale marks instead of a number.
\(g(x)\): a smooth parabola with axis of symmetry at about \(x = 2\) (the 2 does not need to be numbered) and \(g(x) \geqslant 0\) (A1)
Note: Right hand side must not be higher than the maximum of \(f(x)\) at \(x = 4\).
Accept the quadratic correctly drawn beyond \(x = 4\).
Intercept at their numbered \(y = 4\) (A1) (C4)
Note: Accept clear scale marks instead of a number.[4 marks]
\(–0.195, 2.76\) \((–0.194808…, 2.761377…)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A0)(A1)(ft) if both coordinates are given.
Follow through only if \(f(x) = \frac{5}{{{x^2}}} + 1\) is sketched; the solutions are \(–0.841, 3.22\) \((–0.840913…, 3.217747…)\)[2 marks]
Question
Consider the functions \(f(x) = x + 1\) and \(g(x) = {3^x} – 2\).
Write down
(i) the \(x\)-intercept of the graph of \(y = {\text{ }}f(x)\);
(ii) the \(y\)-intercept of the graph of \(y = {\text{ }}g(x)\).[2]
Solve \(f(x) = g(x)\).[2]
Write down the interval for the values of \(x\) for which \(f(x) > g(x)\).[2]
Answer/Explanation
Markscheme
(i) \(( – 1,{\text{ }}0)\) (A1)
Note: Accept \( – 1\).
(ii) \((0,{\text{ }} – 1)\) (A1) (C2)
Note: Accept \( – 1\).
\((x = ){\text{ }} – 2.96{\text{ }}( – 2.96135 \ldots )\) (A1)
\((x = ){\text{ }}1.34{\text{ }}(1.33508 \ldots )\) (A1) (C2)
\( – 2.96 < x < 1.34\;\;\;{\mathbf{OR}}\;\;\;\left] { – 2.96,{\text{ }}1.34} \right[\;\;\;{\mathbf{OR}}\;\;\;( – 2.96,{\text{ }}1.34)\) (A1)(ft)(A1) (C2)
Notes: Award (A1)(ft) for both correct endpoints of the interval, (A1) for correct strict inequalities (or correct open interval notation).
Follow through from part (b).