Question
A submarine is located in a sea at coordinates (0.8, 1.3, −0.3) relative to a ship positioned at the origin O. The x direction is due east, the y direction is due north and the z direction is vertically upwards.
All distances are measured in kilometres.
The submarine travels with direction vector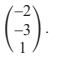 
( a ) Assuming the submarine travels in a straight line, write down an equation for the line
along which it travels. [2]
b (i) Find the coordinates of P.
(ii) Find OP. [5]
▶️Answer/Explanation
(a) r =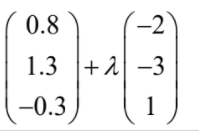 
(b) (i) 0.3 + λ = 0 ⇒ λ = 0.3 
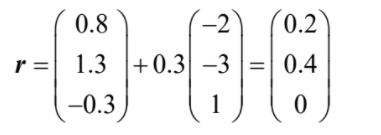P has coordinates (0.2, 0.4, 0) (ii) \(\sqrt{0.2^{2}+ 0.4^{2}}= 0.447 km (=447m)\)
Question
(a) (i) Expand \((\frac{1}{u} + 1)^2\).
(ii) Find \(\int (\frac{1}{x+2}+1)^2 dx\).
The region bounded by \(y = \frac{1}{(x+2)}+1\), x = 0, x = 2 and the x-axis is rotated through \(2\pi\) about the x-axis to form a solid.
(b) Find the volume of the solid formed. Give your answer in the fomr \(\frac{\pi}{4}(a+b In (c))\), where \(a, b , c\epsilon \mathbb{Z}\).
▶️Answer/Explanation
Ans:
(a) (i) \(\frac{1}{u^2}+\frac{2}{u}+1\)
(ii) \(\int (\frac{1}{(x+2)}+1)^2dx
=\int (\frac{1}{(x+2)^2}+\frac{2}{x+2}+1)dx OR \int (\frac{1}{u^2}+\frac{2}{u})du
=-\frac{1}{(x+2)} + 2 In |x+2| + x(+c)\)
Question
P (4, 1) and Q (0, –5) are points on the coordinate plane.
a.Determine the
(i) coordinates of M, the midpoint of P and Q.
(ii) gradient of the line drawn through P and Q.
(iii) gradient of the line drawn through M, perpendicular to PQ.[4]
Find k.[2]
▶️Answer/Explanation
Markscheme
(i) (2, – 2) parentheses not required. (A1)
(ii) gradient of PQ \( = \left( {\frac{{ – 5 – 1}}{{0 – 4}}} \right) = \frac{6}{4} = \frac{3}{2}(1.5)\) (M1)(A1)
(M1) for gradient formula with correct substitution
Award (A1) for \(y = \frac{3}{2}x – 5\) with no other working
(iii) gradient of perpendicular is \( – \frac{2}{3}\) (A1)(ft) (C4)[4 marks]
\(\left( {\frac{{k + 2}}{{0 – 2}}} \right) = – \frac{2}{3}\), \(k = – \frac{2}{3}\) or \(y = – \frac{2}{3}x + c\), \(c = – \frac{2}{3}\therefore k = – \frac{2}{3}\) (M1)(A1)(ft)
Allow (\(0, – \frac{2}{3}\))
(M1) is for equating gradients or substituting gradient into \(y = mx + c\) (C2)[2 marks]
Question
The length of one side of a rectangle is 2 cm longer than its width.
a.If the smaller side is x cm, find the perimeter of the rectangle in terms of x.[1]
b.The length of one side of a rectangle is 2 cm longer than its width.
The perimeter of a square is equal to the perimeter of the rectangle in part (a).
Determine the length of each side of the square in terms of x.[1]
c.The length of one side of a rectangle is 2 cm longer than its width.
The perimeter of a square is equal to the perimeter of the rectangle in part (a).
The sum of the areas of the rectangle and the square is \(2x^2 + 4x +1\) (cm2).
(i) Given that this sum is 49 cm2, find x.
(ii) Find the area of the square.[4]
▶️Answer/Explanation
Markscheme
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) \({\text{P (rectangle)}} = 2x + 2(x + 2) = 4x + 4{\text{ cm}}\) (A1) (C1)
(UP) Simplification not required[1 mark]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) Side of square = (4x + 4)/4 = x + 1 cm (A1)(ft) (C1)[1 mark]
(i) \(2x^2 + 4x + 1 = 49\) or equivalent (M1)
\((x + 6)(x – 4) = 0\)
\(x = – 6\) and \(4\) (A1)
Note: award (A1) for the values or for correct factors
Choose \(x = 4\) (A1)(ft)
Award (A1)(ft) for choosing positive value. (C3)
(ii) \({\text{Area of square}} = 5 \times 5 = 25{\text{ c}}{{\text{m}}^2}\) (A1)(ft)
Note: Follow through from both (b) and (c)(i). (C1)[4 marks]
Question
The mid-point, M, of the line joining A(s , 8) to B(−2, t) has coordinates M(2, 3).
a.Calculate the values of s and t.[2]
b.Find the equation of the straight line perpendicular to AB, passing through the point M.[4]
▶️Answer/Explanation
Markscheme
\(s = 6\) (A1)
\(t = – 2\) (A1) (C2)[2 marks]
\({\text{gradient of AB}} = \frac{{ – 2 – 8}}{{ – 2 – 6}} = \frac{{ – 10}}{{ – 8}} = \frac{5}{4}\) (A1)(ft)
(A1) for gradient of AM or BM \( = \frac{5}{4}\)
\({\text{Perpendicular gradient}} = – \frac{4}{5}\) (A1)(ft)
Equation of perpendicular bisector is
\(y = – \frac{4}{5}x + c\)
\(3 = – \frac{4}{5}(2) + c\) (M1)
\(c = 4.6\)
\(y = -0.8x + 4.6\)
or \(5y = -4x + 23\) (A1)(ft) (C4)[4 marks]