Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.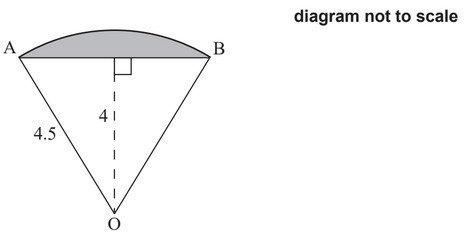
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment.
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.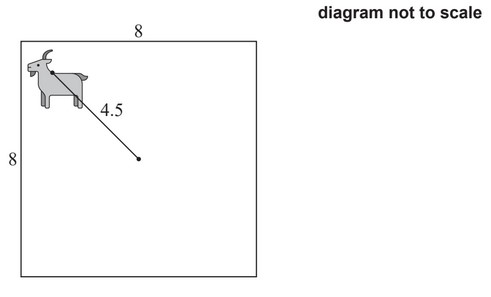
(b) Find the area of the field that can be reached by the goat.
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate.
The goat is tied in the field for 8 hours.
(d) Find the total volume of grass eaten by the goat during this time.
▶️Answer/Explanation
Ans:


Question
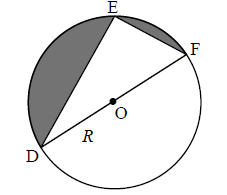
A new triangle DEF is positioned within a circle radius R such that DF is a diameter as shown in the following diagram.
a.i.In a triangle ABC, prove \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}}\).[4]
a.ii.Prove that the area of the triangle ABC is \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\).[2]
a.iii.Given that R denotes the radius of the circumscribed circle prove that \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}} = 2R\).[2]
a.iv.Hence show that the area of the triangle ABC is \(\frac{{abc}}{{4R}}\).[2]
b.i.Find in terms of R, the two values of (DE)2 such that the area of the shaded region is twice the area of the triangle DEF.[9]
b.ii.Using two diagrams, explain why there are two values of (DE)2.[2]
c.A parallelogram is positioned inside a circle such that all four vertices lie on the circle. Prove that it is a rectangle.[3]
▶️Answer/Explanation
Markscheme
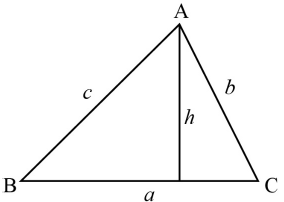
\({\text{sin}}\,{\text{B}} = \frac{h}{c}\) and \({\text{sin}}\,{\text{C}} = \frac{h}{b}\) M1A1
hence \(h = c\,{\text{sin}}\,{\text{B}} = b\,{\text{sin}}\,{\text{C}}\) A1
by dropping a perpendicular from B, in exactly the same way we find \(c\,{\text{sin}}\,{\text{A}} = a\,{\text{sin}}\,{\text{C}}\) R1
hence \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}}\)
[4 marks]
area = \(\frac{1}{2}ah\) M1A1
= \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\) AG
[2 marks]

since the angle at the centre of circle is twice the angle at the circumference \({\text{sin}}\,A = \frac{a}{{2R}}\) M1A1
hence \(\frac{a}{{{\text{sin}}\,A}} = 2R\) and therefore \(\frac{a}{{{\text{sin}}\,A}} = \frac{b}{{{\text{sin}}\,B}} = \frac{c}{{{\text{sin}}\,C}} = 2R\) AG
[2 marks]
area of the triangle is \(\frac{1}{2}ab\,{\text{sin}}\,{\text{C}}\) M1
since \({\text{sin}}\,{\text{C}} = \frac{c}{{2R}}\) A1
area of the triangle is \(\frac{1}{2}ab\,\frac{c}{{2R}} = \frac{{abc}}{{4R}}\) AG
[2 marks]
area of the triangle is \(\frac{{\pi {R^2}}}{6}\) (M1)A1
(DE)2 + (EF)2 = 4R2 M1
(DE)2 = 4R2 − (EF)2
\(\frac{1}{2}\left( {{\text{DE}}} \right)\left( {{\text{EF}}} \right) = \frac{{\pi {R^2}}}{6} \Rightarrow \left( {{\text{EF}}} \right) = \frac{{\pi {R^2}}}{{3\left( {{\text{DE}}} \right)}}\) M1A1
\({\left( {{\text{DE}}} \right)^2} = 4{R^2} – \frac{{{\pi ^2}{R^4}}}{{9{{\left( {{\text{DE}}} \right)}^2}}}\) A1
\(9{\left( {{\text{DE}}} \right)^4} – 36{\left( {{\text{DE}}} \right)^2}{R^2} + {\pi ^2}{R^4} = 0\) A1
\({\left( {{\text{DE}}} \right)^2} = \frac{{36{R^2} \pm \sqrt {1296{R^4} – 36{\pi ^2}{R^4}} }}{{18}}\) M1
\({\left( {{\text{DE}}} \right)^2} = \frac{{36{R^2} \pm 6{R^2}\sqrt {36 – {\pi ^2}} }}{{18}}\left( { = \frac{{6{R^2} \pm {R^2}\sqrt {36 – {\pi ^2}} }}{3}} \right)\) A1
[9 marks]
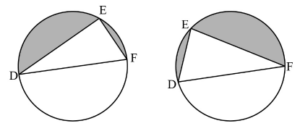 A1A1
A1A1
[2 marks]
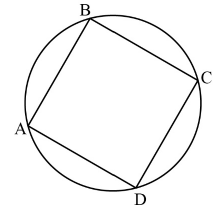
\(\mathop {\text{A}}\limits^ \wedge + \mathop {\text{C}}\limits^ \wedge = 180^\circ \) (cyclic quadrilateral) R1
however \(\mathop {\text{A}}\limits^ \wedge = \mathop {\text{C}}\limits^ \wedge \) (ABCD is a parallelogram) R1
\(\mathop {\text{A}}\limits^ \wedge = \mathop {\text{C}}\limits^ \wedge = 90^\circ \) A1
\(\mathop {\text{B}}\limits^ \wedge = \mathop {\text{D}}\limits^ \wedge = 90^\circ \)
hence ABCD is a rectangle AG
[3 marks]
Question
A circle \(C\) passes through the point \((1,{\text{ }}2)\) and has the line \(3x – y = 5\) as the tangent at the point \((3,{\text{ }}4)\).
a.Find the coordinates of the centre of \(C\) and its radius.[9]
b.Write down the equation of \(C\).[1]
c.Find the coordinates of the second point on \(C\) on the chord through \((1,{\text{ }}2)\) parallel to the tangent at \((3,{\text{ }}4)\).[5]
▶️Answer/Explanation
Markscheme
METHOD 1
attempt to exploit the fact that the normal to a tangent passes through the centre \((a,{\text{ }}b)\) (M1)
EITHER
equation of normal is \(y – 4 = – \frac{1}{3}(x – 3)\) (A1)
obtain \(a + 3b = 15\) A1
attempt to exploit the fact that a circle has a constant radius: (M1)
obtain \({(1 – a)^2} + {(2 – b)^2} = {(3 – a)^2} + {(4 – b)^2}\) A1
leading to \(a + b = 5\) A1
centre is \((0,{\text{ }}5)\) (M1)A1
radius \( = \sqrt {{1^2} + {3^2}} = \sqrt {10} \) A1
OR
gradient of normal \( = – \frac{1}{3}\) A1
general point on normal \( = (3 – 3\lambda ,{\text{ }}4 + \lambda )\) (M1)A1
this point is equidistant from \((1,{\text{ }}2)\) and \((3,{\text{ }}4)\) M1
if \(10{\lambda ^2} = {(2 – 3\lambda )^2} + {(2 + \lambda )^2}\)
\(10{\lambda ^2} = 4 – 12\lambda + 9{\lambda ^2} + 4 + 4\lambda + {\lambda ^2}\) A1
\(\lambda = 1\) A1
centre is \((0,{\text{ }}5)\) A1
radius \( = \sqrt {10\lambda } = \sqrt {10} \) A1
METHOD 2
attempt to substitute two points in the equation of a circle (M1)
\({(1 – h)^2} + {(2 – k)^2} = {r^2},{\text{ }}{(3 – h)^2} + {(4 – k)^2} = {r^2}\) A1
Note: The A1 is for the two LHSs, which may be seen equated.
equate or subtract the equations
obtain \(h + k = 5\) or equivalent A1
attempt to differentiate the circle equation implicitly (M1)
obtain \(2(x – h) + 2(y – k)\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) A1
Note: Similarly, M1A1 if direct differentiation is used.
substitute \((3,{\text{ }}4)\) and gradient \( = 3\) to obtain \(h + 3k = 15\) A1
obtain centre \( = (0,{\text{ }}5)\) (M1)A1
radius \( = \sqrt {10} \) A1
[9 marks]
equation of circle is \({x^2} + {(y – 5)^2} = 10\) A1
[1 mark]
the equation of the chord is \(3x – y = 1\) A1
attempt to solve the equation for the chord and that for the circle simultaneously (M1)
for example \({x^2} + {(3x – 1 – 5)^2} = 10\) A1
coordinates of the second point are \(\left( {\frac{{13}}{5},{\text{ }}\frac{{34}}{5}} \right)\) (M1)A1
[5 marks]
Question
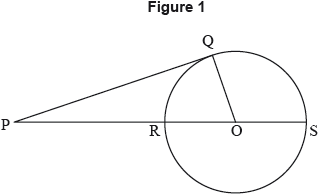
Figure 1 shows a tangent [PQ] at the point Q of a circle and a line [PS] meeting the circle at the points R , S and passing through the centre O of the circle.
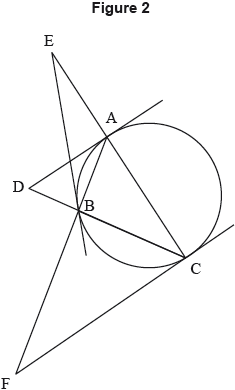
Figure 2 shows a triangle ABC inscribed in a circle. The tangents at the points A , B , C meet the opposite sides of the triangle externally at the points D , E , F respectively.
a.i.Show that \({\text{P}}{{\text{Q}}^2} = {\text{PR}} \times {\text{PS}}\).[2]
a.ii.State briefly how this result can be generalized to give the tangent-secant theorem.[2]
b.i.Show that \(\frac{{{\text{A}}{{\text{D}}^2}}}{{{\text{B}}{{\text{D}}^2}}} = \frac{{{\text{CD}}}}{{{\text{BD}}}}\).[2]
b.ii.By considering a pair of similar triangles, show that
\(\frac{{{\text{AD}}}}{{{\text{BD}}}} = \frac{{{\text{AC}}}}{{{\text{AB}}}}\) and hence that \(\frac{{{\text{CD}}}}{{{\text{BD}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}}\).[2]
b.iii.By writing down and using two further similar expressions, show that the points D, E, F are collinear.[6]
▶️Answer/Explanation
Markscheme
let \(r = \) radius of circle. Consider
\({\text{PR}} \times {\text{PS}} = ({\text{PO}} – r)({\text{PO}} + r)\) M1
\( = {\text{P}}{{\text{O}}^2} – {\text{O}}{{\text{Q}}^2}\) A1
\( = {\text{P}}{{\text{Q}}^2}\) because POQ is a right angled triangle R1
[2 marks]
the result is true even if PS does not pass through O A1
[2 marks]
using the tangent-secant theorem, M1
\({\text{A}}{{\text{D}}^2} = {\text{BD}} \times {\text{CD}}\) A1
so \(\frac{{{\text{A}}{{\text{D}}^2}}}{{{\text{B}}{{\text{D}}^2}}} = \frac{{{\text{CD}}}}{{{\text{BD}}}} \ldots {\text{ (1)}}\) AG
[??? marks]
consider the triangles CAD and ABD. They are similar because M1
\({\rm{D\hat AB}} = {\rm{A\hat CD}}\), angle \({\rm{\hat D}}\) is common therefore the third angles must be equal A1
Note: Beware of the assumption that AC is a diameter of the circle.
therefore
\(\frac{{{\text{AD}}}}{{{\text{BD}}}} = \frac{{{\text{AC}}}}{{{\text{AB}}}} \ldots {\text{ (2)}}\) AG
it follows from (1) and (2) that
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}}\) AG
[??? marks]
two similar expressions are
\(\frac{{{\text{AE}}}}{{{\text{CE}}}} = \frac{{{\text{B}}{{\text{A}}^2}}}{{{\text{B}}{{\text{C}}^2}}}\) M1A1
\(\frac{{{\text{BF}}}}{{{\text{AF}}}} = \frac{{{\text{C}}{{\text{B}}^2}}}{{{\text{C}}{{\text{A}}^2}}}\) A1
multiplying the three expressions,
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} \times \frac{{{\text{AE}}}}{{{\text{CE}}}} \times \frac{{{\text{BF}}}}{{{\text{AF}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}} \times \frac{{{\text{B}}{{\text{A}}^2}}}{{{\text{B}}{{\text{C}}^2}}} \times \frac{{{\text{C}}{{\text{B}}^2}}}{{{\text{C}}{{\text{A}}^2}}}\) M1
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} \times \frac{{{\text{AE}}}}{{{\text{CE}}}} \times \frac{{{\text{BF}}}}{{{\text{AF}}}} = 1\) A1
it follows from the converse of Menelaus’ theorem (ignoring signs) R1
that D, E, F are collinear AG
[??? marks]
Question
A.Prove that the interior bisectors of two of the angles of a non-isosceles triangle and the exterior bisector of the third angle, meet the sides of the triangle in three collinear points.[8]
B.a.An equilateral triangle QRT is inscribed in a circle. If S is any point on the arc QR of the circle,
(i) prove that \({\rm{ST}} = {\rm{SQ}} + {\rm{SR}}\) ;
(ii) show that triangle RST is similar to triangle PSQ where P is the intersection of [TS] and [QR];
(iii) using your results from parts (i) and (ii) deduce that \(\frac{1}{{{\rm{SP}}}} = \frac{1}{{{\rm{SQ}}}} + \frac{1}{{{\rm{SR}}}}\) .[10]
B.b.Perpendiculars are drawn from a point P on the circumcircle of triangle LMN to the three sides. The perpendiculars meet the sides [LM], [MN] and [LN] at the points E, F and G respectively.
Prove that \({\rm{PL}} \times {\rm{PF}} = {\rm{PM}} \times {\rm{PG}}\) .[8]
▶️Answer/Explanation
Markscheme
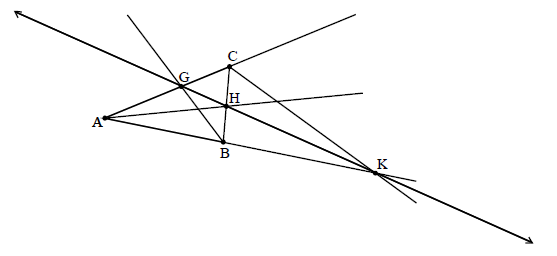
triangle ABC has interior angle bisectors AH, BG and exterior angle bisector CK
using the angle bisector theorem, M1
\(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} = \frac{{{\rm{CA}}}}{{{\rm{AB}}}}\) , \(\frac{{{\rm{AG}}}}{{{\rm{GC}}}} = \frac{{{\rm{AB}}}}{{{\rm{CB}}}}\) , \(\frac{{{\rm{BK}}}}{{{\rm{AK}}}} = \frac{{{\rm{CB}}}}{{{\rm{CA}}}}\) A2
hence, \(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} \times \frac{{{\rm{AG}}}}{{{\rm{GC}}}} \times \frac{{{\rm{BK}}}}{{{\rm{AK}}}} = \frac{{{\rm{CA}}}}{{{\rm{AB}}}} \times \frac{{{\rm{AB}}}}{{{\rm{CB}}}} \times \frac{{{\rm{CB}}}}{{{\rm{CA}}}} = 1\) M1A1
but \(\frac{{{\rm{BK}}}}{{{\rm{AK}}}} = – \frac{{{\rm{BK}}}}{{{\rm{KA}}}}\) R1
so, \(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} \times \frac{{{\rm{AG}}}}{{{\rm{GC}}}} \times \frac{{{\rm{BK}}}}{{{\rm{AK}}}} = – 1\) A1
hence, by converse Menelaus’ theorem, G, H and K are collinear R1[8 marks]
(i)
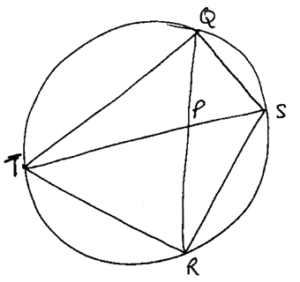
\({\rm{ST}} \bullet {\rm{QR}} = {\rm{SQ}} \bullet {\rm{RT}} + {\rm{SR}} \bullet {\rm{QT}}\) M1A1
but \({\rm{QT = QR = RT}}\) R1
hence \({\rm{ST = SQ + SR}}\) AG
(ii) \(\angle {\rm{STR = }}\angle {\rm{SQR}}\) R1
\(\angle {\rm{QST = }}\angle {\rm{QRT = }}{60^ \circ }\) A1
\(\angle {\rm{RST = }}\angle {\rm{RQT = }}{60^ \circ }\) A1
hence \(\angle {\rm{QST = }}\angle {\rm{RST}}\) and \(\Delta {\rm{RST}} \sim \Delta {\rm{PSQ}}\) R1
(iii) \(\frac{{{\rm{ST}}}}{{{\rm{SQ}}}} = \frac{{{\rm{SR}}}}{{{\rm{SP}}}} \to {\rm{ST}} \times {\rm{SP}} = {\rm{SR}} \times {\rm{SQ}}\) M1A1
but \({\rm{ST = (SQ + SR)}}\)
\({\rm{(SQ}} + {\rm{SR) \times SP}} = {\rm{SR}} \times {\rm{SQ}}\) A1
\({\rm{SQ}} \times {\rm{SP}} + {\rm{SR}} \times {\rm{SP}} = {\rm{SR}} \times {\rm{SQ}}\)
hence \(\frac{1}{{{\rm{SP}}}} = \frac{1}{{{\rm{SQ}}}} + \frac{1}{{{\rm{SR}}}}\) AG
[10 marks]
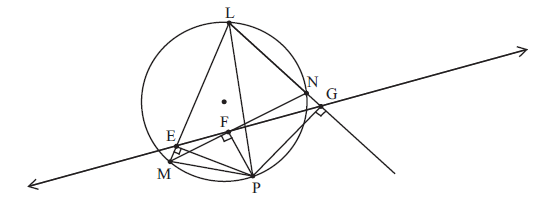
sine \(m\angle {\rm{PEM}} \cong m\angle {\rm{PFM}} \cong {90^ \circ }\)
then quadrilateral PFEM is cyclic M1A1
so \(m\angle {\rm{PME}} \cong m\angle {\rm{PFG}}\)
since \(m\angle {\rm{PGL}} \cong m\angle {\rm{PEL}} \cong {90^ \circ }\)
then quadrilateral PGLE is cyclic
so \(m\angle {\rm{PGE}} \cong m\angle {\rm{PLE}}\) R1A1
now E, F and G are collinear since they are on the Simson line of \(\Delta {\rm{LMN}}\) R1
hence \(\Delta {\rm{PFG}} \sim \Delta {\rm{PML}}\) A1
so \(\frac{{{\rm{PL}}}}{{{\rm{PM}}}} = \frac{{{\rm{PG}}}}{{{\rm{PF}}}} \Rightarrow {\rm{PL}} \times {\rm{PF}} = {\rm{PM}} \times {\rm{PG}}\) R1AG
[8 marks]
B.b.
