Question
A vertical pole stands on horizontal ground. The bottom of the pole is taken as the origin, O,
of a coordinate system in which the top, F, of the pole has coordinates (0, 0, 5.8). All units
are in metres.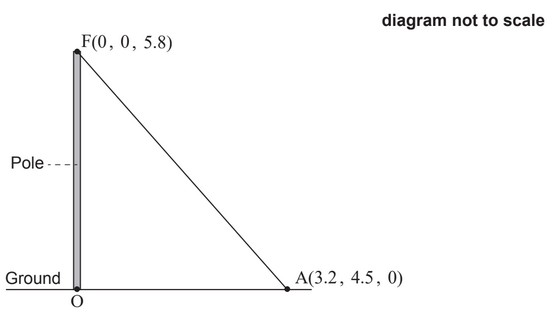
The pole is held in place by ropes attached at F.
One of the ropes is attached to the ground at a point A with coordinates (3.2, 4.5, 0).
The rope forms a straight line from A to F.
(a) Find the length of the rope connecting A to F.
(b) Find \(F \widehat{A} O\), the angle the rope makes with the ground.
Answer/Explanation
Ans:
(a) \(\sqrt{3.2^2 + 4.5^2 +5.8^2}\)
=8.01 (8.00812…) m
(b) \(F\widehat{A} O = sin^{-1} (\frac{5.8}{8.00812…})\) OR \(cos^{-1}(\frac{5.52177…}{8.00812…})\) OR \(tan^{-1}(\frac{5.8}{5.52177…})\)
\(46.4^o (46.4077…^o)\)
Question
State which of the following sets of data are discrete.
(i) Speeds of cars travelling along a road.
(ii) Numbers of members in families.
(iii) Maximum daily temperatures.
(iv) Heights of people in a class measured to the nearest cm.
(v) Daily intake of protein by members of a sporting team.[2]
The boxplot below shows the statistics for a set of data.
For this data set write down the value of
(i) the median
(ii) the upper quartile
(iii) the minimum value present[3]
Write down three different integers whose mean is 10.[1]
Answer/Explanation
Markscheme
(ii) and (iv) are discrete. (A1)(A1)
Award (A1)(A0) for both correct and one incorrect.
Award (A1)(A0) for one correct and two incorrect.
Otherwise, (A0)(A0). (C2)[2 marks]
(i) Median = 10 (A1)
(ii) Q3 = 12 (A1)
(iii) Min value = 1 (±0.2) (A1) (C3)[3 marks]
Any three different integers whose mean is 10 e.g. 9, 10, 11. (A1) (C1)[1 mark]
Question
A survey was conducted of the number of bedrooms in \(208\) randomly chosen houses. The results are shown in the following table.
State whether the data is discrete or continuous.[1]
Write down the mean number of bedrooms per house.[2]
Write down the standard deviation of the number of bedrooms per house.[1]
Find how many houses have a number of bedrooms greater than one standard deviation above the mean.[2]
Answer/Explanation
Markscheme
Discrete (A1) (C1)[1 mark]
For attempting to find \(\sum fx/\sum f\) (M1)
\(2.73\) (A1) (C2)
Note: for (b) and (c), if both mean and standard deviation given to 2 significant figures.
Award (C1)(C0)(AP) for \(2.7\). Award (A1)(ft) for \(1.3\) ((AP) already deducted).[2 marks]
\(1.34\) (A1) (C1)
Note: for (b) and (c), if both mean and standard deviation given to 2 significant figures.
Award (C1)(C0)(AP) for \(2.7\). Award (A1)(ft) for \(1.3\) ((AP) already deducted).[1 mark]
Attempt to find their mean \( + \) their standard deviation (can be implied) (M1)
\(23\), (ft) their mean and standard deviation. (A1)(ft) (C2)[2 marks]
Question
The following table shows the number of errors per page in a 100 page document.
State whether the data is discrete, continuous or neither.[1]
Find the mean number of errors per page.[2]
Find the median number of errors per page.[2]
Write down the mode.[1]
Answer/Explanation
Markscheme
Discrete (A1) (C1)[1 mark]
\(\frac{{0 + 24 + 40 + 51 + 44}}{{100}} = \frac{{159}}{{100}} = 1.59\) (M1)(A1) (C2)
Notes: Award (M1) for correctly substituted formula.
Award (M1)(A1) for 1 or 2 if 1.59 is seen.
Award (M0)(A0) for 1 or 2 seen with no working.[2 marks]
1 (M1)(A1) (C2)
Note: Award (M1) for attempt to order raw data (if frequency table not used) or (M1) for indicating halfway between 50th and 51st result or (M1) for 50th percentile seen.[2 marks]
0 (A1) (C1)[1 mark]
Question
A survey was carried out on a road to determine the number of passengers in each car (excluding the driver). The table shows the results of the survey.

State whether the data is discrete or continuous.[1]
Write down the mode.[1]
Use your graphic display calculator to find
(i) the mean number of passengers per car;
(ii) the median number of passengers per car;
(iii) the standard deviation.[4]
Answer/Explanation
Markscheme
discrete (A1) (C1)[1 mark]
(i) \(1.47\) \((1.46666…)\) (A2)
Note: Award (M1) for \(\frac{{176}}{{120}}\) seen.
Accept \(1\) or \(2\) as a final answer if \(1.4666…\) or \(1.47\) seen.
(ii) \(1.5\) (A1)
(iii) \(1.25\) \((1.25122…)\) (A1) (C4)[4 marks]
Question
In a particular week, the number of eggs laid by each hen on a farm was counted. The results are summarized in the following table.

State whether these data are discrete or continuous.[1]
Write down
(i) the number of hens on the farm;
(ii) the modal number of eggs laid.[2]
Calculate
(i) the mean number of eggs laid;
(ii) the standard deviation.[3]
Answer/Explanation
Markscheme
discrete (A1) (C1)
(i) 60 (A1)
(ii) 5 (A1) (C2)
(i) \(\frac{{1 \times 4 + 2 \times 7 + 3 \times 12 \ldots }}{{60}}\) (M1)
Notes: Award (M1) for an attempt to substitute into the “mean of a set of data” formula, with at least three correct terms in the numerator.
Denominator must be 60.
Follow through from part (b)(i), only if work is seen.
\( = 4.03{\text{ }}(4.03333 \ldots )\) (A1)
Notes: Award at most (M1)(A0) for an answer of 4 but only if working seen.
(ii) \(1.54{\text{ }}(1.53803 \ldots )\) (A1) (C3)
