Question 5. [Maximum mark: 5]
The number of sick days taken by each employee in a company during a year was recorded. The data was organized in a box and whisker diagram as shown below:
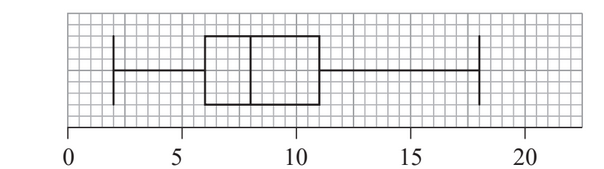
For this data,
(i)write down the minimum number of sick days taken during the year.
(ii)the lower quartile.
(iii)the median. [3]
Paul claims that this box and whisker diagram can be used to infer that the percentage of employees who took fewer than six sick days is smaller than the percentage of employees who took more than eleven sick days.
b. State whether Paul is correct. Justify your answer. [2]
▶️Answer/Explanation
(a) (i) 2 (ii) 6 (iii) 8
(b) EITHER Each of these percentages represent approximately 25% of the employees. OR
The diagram is not explicit enough to show what is happening at the quartiles regarding 6 and 11 / we do not have the data points OR
Discrete data not clear how to interpret “fewer”. THEN Hence, Paul is not correct (OR no such inference can be made).
Question 2 [Maximum mark: 4]
Deb used a thermometer to record the maximum daily temperature over ten consecutive days. Her results, in degrees Celsius (°C), are shown below.
14 , 15 , 14 , 11 , 10 , 9 , 14 , 15 , 16 , 13
For this data set, find the value of
(i)the mode. [1]
(ii)the mean. [2]
(iii)the standard deviation. [1]
▶️Answer/Explanation
(a) \(14\)
(b)\(\frac{14+15+..}{10 }=13.1 \)
(c) 2.21(2.21133..)
Question
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
a.(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.[3]
b.Calculate \(\sqrt {{{3.87}^5} – {{8.73}^{ – 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .[3]
▶️Answer/Explanation
Markscheme
(i) Mean = (5.96 + 5.95 + 6.02 + 5.95 + 5.99) / 5 = 5.974 (5.97) (A1)
(ii) \({\text{% error}} = \frac{{error}}{{actualvalue}} \times 100\% \)
\( = \frac{{6 – 5.974}}{{5.974}} \times 100\% = 0.435\% \) (M1)(A1)(ft)
(M1) for correctly substituted formula.
Allow 0.503% as follow through from 5.97
Note: An answer of 0.433% is incorrect. (C3)[3 marks]
number is 29.45728613
(i) Nearest integer = 29 (A1)
(ii) Standard form = 2.95 × 101 (accept 2.9 × 101) (A1)(ft)(A1)
Award (A1) for each correct term
Award (A1)(A0) for 2.95 × 10 (C3)[3 marks]
Question
State which of the following sets of data are discrete.
a.(i) Speeds of cars travelling along a road.
(ii) Numbers of members in families.
(iii) Maximum daily temperatures.
(iv) Heights of people in a class measured to the nearest cm.
(v) Daily intake of protein by members of a sporting team.[2]
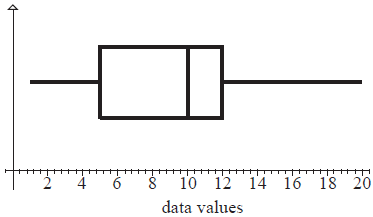
For this data set write down the value of
c(i) the median
(ii) the upper quartile
(iii) the minimum value present[3]
c.Write down three different integers whose mean is 10.[1]
▶️Answer/Explanation
Markscheme
(ii) and (iv) are discrete. (A1)(A1)
Award (A1)(A0) for both correct and one incorrect.
Award (A1)(A0) for one correct and two incorrect.
Otherwise, (A0)(A0). (C2)[2 marks]
(i) Median = 10 (A1)
(ii) Q3 = 12 (A1)
(iii) Min value = 1 (±0.2) (A1) (C3)[3 marks]
Any three different integers whose mean is 10 e.g. 9, 10, 11. (A1) (C1)[1 mark]
Question
State which of the following sets of data are discrete.
a.(i) Speeds of cars travelling along a road.
(ii) Numbers of members in families.
(iii) Maximum daily temperatures.
(iv) Heights of people in a class measured to the nearest cm.
(v) Daily intake of protein by members of a sporting team.[2]

For this data set write down the value of
c(i) the median
(ii) the upper quartile
(iii) the minimum value present[3]
c.Write down three different integers whose mean is 10.[1]
▶️Answer/Explanation
Markscheme
(ii) and (iv) are discrete. (A1)(A1)
Award (A1)(A0) for both correct and one incorrect.
Award (A1)(A0) for one correct and two incorrect.
Otherwise, (A0)(A0). (C2)[2 marks]
(i) Median = 10 (A1)
(ii) Q3 = 12 (A1)
(iii) Min value = 1 (±0.2) (A1) (C3)[3 marks]
Any three different integers whose mean is 10 e.g. 9, 10, 11. (A1) (C1)[1 mark]
Question
State which of the following sets of data are discrete.
a.(i) Speeds of cars travelling along a road.
(ii) Numbers of members in families.
(iii) Maximum daily temperatures.
(iv) Heights of people in a class measured to the nearest cm.
(v) Daily intake of protein by members of a sporting team.[2]

For this data set write down the value of
c(i) the median
(ii) the upper quartile
(iii) the minimum value present[3]
c.Write down three different integers whose mean is 10.[1]
▶️Answer/Explanation
Markscheme
(ii) and (iv) are discrete. (A1)(A1)
Award (A1)(A0) for both correct and one incorrect.
Award (A1)(A0) for one correct and two incorrect.
Otherwise, (A0)(A0). (C2)[2 marks]
(i) Median = 10 (A1)
(ii) Q3 = 12 (A1)
(iii) Min value = 1 (±0.2) (A1) (C3)[3 marks]
Any three different integers whose mean is 10 e.g. 9, 10, 11. (A1) (C1)[1 mark]
Question
a.Write down the following numbers in increasing order.
\(3.5\), \(1.6 \times 10^{−19}\), \(60730\), \(6.073 \times 10^{5}\), \(0.006073 \times 10^6\), \(\pi\), \(9.8 \times 10^{−18}\).[3]
b.Write down the median of the numbers in part (a).[1]
▶️Answer/Explanation
Markscheme
\(1.6 \times 10^{−19}\), \(9.8 \times 10^{−18}\), \(\pi\), \(3.5\), \(0.006073 \times 10^6\), \(60730\), \(6.073 \times 10^{5}\) (A4)
Award (A1) for \(\pi\) before 3.5
Award (A1) for \(1.6 \times 10^{−19}\) before \(9.8 \times 10^{−18}\)
Award (A1) for the three numbers containing 6073 in the correct order.
Award (A1) for the pair with negative indices placed before 3.5 and \(\pi\) and the remaining three numbers placed after (independently of the other three marks).
Award (A3) for numbers given in correct decreasing order.
Award (A2) for decreasing order with at most 1 error (C4)[3 marks]
The median is 3.5. (A1)(ft)
Follow through from candidate’s list. (C1)[1 mark]
\(\pi\) is irrational. (A1) (C1)[1 mark]
