Question 1 [Maximum mark: 18]
As part of his mathematics exploration about classic books, Jason investigated the time taken by students in his school to read the book The Old Man and the Sea. He collected his data by
stopping and asking students in the school corridor, until he reached his target of 10 students from each of the literature classes in his school.
State which of the two sampling methods, systematic or quota, Jason has used. [1]
Jason constructed the following box and whisker diagram to show the number of hours students in the sample took to read this book.
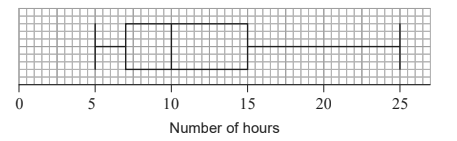
Write down the median time to read the book. [1]
Calculate the interquartile range. [2]
Mackenzie, a member of the sample, took 25 hours to read the novel. Jason believes Mackenzie’s time is not an outlier.
Determine whether Jason is correct. Support your reasoning. [4] For each student interviewed, Jason recorded the time taken to read The Old Man and the
Sea ( x ), measured in hours, and paired this with their percentage score on the final exam ( y ).
These data are represented on the scatter diagram.
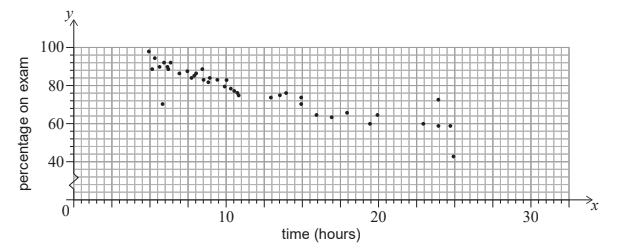
Describe the correlation. [1]
Jason correctly calculates the equation of the regression line y on x for these students to be
y = -1.54x + 98.8 .
He uses the equation to estimate the percentage score on the final exam for a student who read the book in 1.5 hours.
Find the percentage score calculated by Jason. [2]
State whether it is valid to use the regression line y on x for Jason’s estimate. Give a reason for your answer. [2]
Jason found a website that rated the ‘top 50’ classic books. He randomly chose eight of these classic books and recorded the number of pages. For example, Book H is rated 44th and has 281 pages. These data are shown in the table.

Jason intends to analyse the data using Spearman’s rank correlation coefficient, rs .
Copy and complete the information in the following table. [2]

(i) Calculate the value of rs .
(ii) Interpret your result. [3]
Answer/Explanation
(a) Quota sampling
(b) 10(hours) (c) 15 – 7 = 8
(d) indication of a valid attempt to find the upper fence 15 + 1.5 × 8 = 27 25 27 < (accept equivalent answer in words) Jason is correct
(e) “negative” seen (f) correct substitution y =− 1.54 × 1.5 + 98.8 96.5 (%) (96.49)
(g) not reliable extrapolation OR outside the given range of the data
(h) 
(i) (i) 0.714 (0.714285…)
(ii) EITHER
there is a (strong/moderate) positive association between the number of pages an the top 50 rating. OR there is a (strong/moderate) agreement between the rank order of number of pages and the rank order top 50 rating. OR there is a (strong/moderate) positive (linear) correlation between the rank order of number of pages and the rank order top 50 rating.
Question
The scores of the eight highest scoring countries in the 2019 Eurovision song contest are
shown in the following table.
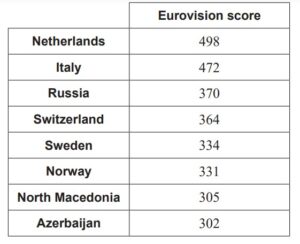
(a) For this data, find
(i) the upper quartile.
(ii) the interquartile range. [4]
(b) Determine if the Netherlands’ score is an outlier for this data. Justify your answer. [3]
(Question 3 continued)
Chester is investigating the relationship between the highest-scoring countries’ Eurovision
score and their population size to determine whether population size can reasonably be
used to predict a country’s score.
The populations of the countries, to the nearest million, are shown in the table.
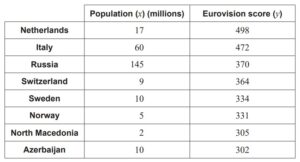
Chester finds that, for this data, the Pearson’s product moment correlation coefficient
is r = 0.249.
(c) State whether it would be appropriate for Chester to use the equation of a regression
line for y on x to predict a country’s Eurovision score. Justify your answer. [2]
Chester then decides to find the Spearman’s rank correlation coefficient for this data,
and creates a table of ranks.
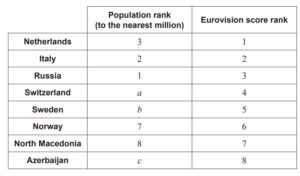
(Question 3 continued)
(d) Write down the value of:
(i) a ,
(ii) b ,
(iii) c . [3]
(e) (i) Find the value of the Spearman’s rank correlation coefficient rs .
(ii) Interpret the value obtained for rs . [3]
(f) When calculating the ranks, Chester incorrectly read the Netherlands’ score as 478.
Explain why the value of the Spearman’s rank correlation rs does not change despite
this error. [1]
Answer/Explanation
Ans
3. (a) (i) \(\frac{370+472}{2}\) (M1)
Note: This (M1) can also be awarded for either a correct Q3 or a correct Q1
in part (a)(ii).
Q3 = 421 A1
(ii) their part (a)(i) – their Q1 (clearly stated) (M1)
IQR = (421 – 318 = ) 103 A1
[4 marks]
(b) (Q3 + 1.5 (IQR) =) 421 + 1.5 × 103) (M1)
= 575.5
since 498<575.5 R1
Netherlands is not an outlier A1
Note: The R1 is dependent on the (M1). Do not award R0A1 [3 marks]
(c) not appropriate (“no” is sufficient) A1
as r is too close to zero / too weak a correlation R1
[2 marks]
(d) (i) 6 A1
(ii) 4.5 A1
(iii) 4.5 A1
[3 marks]
(e) (i) rs = 0.683 (0.682646…) A2
(ii) EITHER
there is a (positive) association between the population size and
the score A1
OR
there is a (positive) linear correlation between the ranks of the population size
and the ranks of the scores (when compared with the PMCC of 0.249). A1
[3 marks]
(f) lowering the top score by 20 does not change its rank so rs is unchanged R1
Note: Accept “this would not alter the rank” or “Netherlands still top rank” or similar.
Condone any statement that clearly implies the ranks have not changed, for
example: “The Netherlands still has the highest score.”
[1 mark]
[Total 16 marks]
Question
The number of bottles of water sold at a railway station on each day is given in the following table.
Write down
(i) the mean temperature;
(ii) the standard deviation of the temperatures.[2]
Write down the correlation coefficient, \(r\), for the variables \(n\) and \(T\).[1]
Comment on your value for \(r\).[2]
The equation of the line of regression for \(n\) on \(T\) is \(n = dT – 100\).
(i) Write down the value of \(d\).
(ii) Estimate how many bottles of water will be sold when the temperature is \({19.6^ \circ }\).[2]
On a day when the temperature was \({36^ \circ }\) Peter calculates that \(314\) bottles would be sold. Give one reason why his answer might be unreliable.[1]
Answer/Explanation
Markscheme
(i) 19.2 (G1)
(ii) 1.45 (G1)[2 marks]
\(r = 0.942\) (G1)[1 mark]
Strong, positive correlation. (A1)(ft)(A1)(ft)[2 marks]
(i) \(d = 11.5\) (G1)
(ii) \(n = 11.5 \times 19.6 – 100\)
\( = 125\) (accept \(126\)) (A1)(ft)
Note: Answer must be a whole number.[2 marks]
It is unreliable to extrapolate outside the values given (outlier). (R1)[1 mark]
Question
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
In a study on \(100\) students there seemed to be a difference between males and females in their choice of favourite car colour. The results are given in the table below. A \(\chi^2\) test was conducted.
Use your graphic display calculator to find the mean number of trees.[1]
Use your graphic display calculator to find the mean depth of snow.[1]
Use your graphic display calculator to find the standard deviation of the depth of snow.[1]
The covariance, Sxy = 188.5.
Write down the product-moment correlation coefficient, r.[2]
Write down the equation of the regression line of y on x.[2]
If the number of trees in an area is 55, estimate the depth of snow.[2]
Use the equation of the regression line to estimate the depth of snow in an area with 100 trees.[1]
Decide whether the answer in (e)(i) is a valid estimate of the depth of snow in the area. Give a reason for your answer.[2]
Write down the total number of male students.[1]
Show that the expected frequency for males, whose favourite car colour is blue, is 12.6.[2]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the null hypothesis for this test.[1]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the number of degrees of freedom.[1]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Determine whether the null hypothesis should be accepted at the \(5\%\) significance level. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
50 (G1)[1 mark]
30.5 (G1)[1 mark]
12.3 (G1)
Note: Award (A1)(ft) for 13.0 in (iv) but only if 17.7 seen in (a)(ii).[1 mark]
\(r = \frac{{188.5}}{{(16.79 \times 12.33)}}\) (M1)
Note: Award (M1) for using their values in the correct formula.
= 0.911 (accept 0.912, 0.910) (A1)(ft)(G2)[2 marks]
y = 0.669x − 2.95 (G1)(G1)
Note: Award (G1) for 0.669x, (G1) for −2.95. If the answer is not in the form of an equation, award at most (G1)(G0).[2 marks]
Depth = 0.669 × 55 − 2.95 (M1)
= 33.8 (A1)(ft)(G2)(ft)
Note: Follow through from their (c) even if no working seen.[2 marks]
64.0 (accept 63.95, 63.9) (A1)(ft)(G1)(ft)
Note: Follow through from their (c) even if no working seen.[1 mark]
It is not valid. It lies too far outside the values that are given. Or equivalent. (A1)(R1)
Note: Do not award (A1)(R0).[2 marks]
28 (A1)[1 mark]
\(\frac{{28 \times 45}}{{100}}\left( {\frac{{28}}{{100}} \times \frac{{45}}{{100}} \times 100} \right)\) (M1)(A1)(ft)
Note: Award (M1) for correct formula, (A1) for correct substitution.
= 12.6 (AG)
Note: Do not award (A1) unless 12.6 seen.[2 marks]
the favourite car colour is independent of gender. (A1)
Note: Accept there is no association between gender and favourite car colour.
Do not accept ‘not related’ or ‘not correlated’.[1 mark]
\(2\) (A1)[1 marks]
Accept the null hypothesis since \(1.367 < 5.991\) (A1)(ft)(R1)
Note: Allow “Do not reject”. Follow through from their null hypothesis and their critical value.
Full credit for use of \(p\)-values from GDC [\(p = 0.505\)].
Do not award (A1)(R0). Award (R1) for valid comparison.[2 marks]
Question
Francesca is a chef in a restaurant. She cooks eight chickens and records their masses and cooking times. The mass m of each chicken, in kg, and its cooking time t, in minutes, are shown in the following table.
Draw a scatter diagram to show the relationship between the mass of a chicken and its cooking time. Use 2 cm to represent 0.5 kg on the horizontal axis and 1 cm to represent 10 minutes on the vertical axis.[4]
Write down for this set of data
(i) the mean mass, \(\bar m\) ;
(ii) the mean cooking time, \(\bar t\) .[2]
Label the point \({\text{M}}(\bar m,\bar t)\) on the scatter diagram.[1]
Draw the line of best fit on the scatter diagram.[2]
Using your line of best fit, estimate the cooking time, in minutes, for a 1.7 kg chicken.[2]
Write down the Pearson’s product–moment correlation coefficient, r .[2]
Using your value for r , comment on the correlation.[2]
The cooking time of an additional 2.0 kg chicken is recorded. If the mass and cooking time of this chicken is included in the data, the correlation is weak.
(i) Explain how the cooking time of this additional chicken might differ from that of the other eight chickens.
(ii) Explain how a new line of best fit might differ from that drawn in part (d).[2]
Answer/Explanation
Markscheme
(A1) for correct scales and labels (mass or m on the horizontals axis, time or t on the vertical axis)
(A3) for 7 or 8 correctly placed data points
(A2) for 5 or 6 correctly placed data points
(A1) for 3 or 4 correctly placed data points, (A0) otherwise. (A4)
Note: If axes reversed award at most (A0)(A3)(ft). If graph paper not used, award at most (A1)(A0).
(i) 1.91 (kg) (1.9125 kg) (G1)
(ii) 83 (minutes) (G1)
Their mean point labelled. (A1)(ft)
Note: Follow through from part (b). Accept any clear indication of the mean point. For example: circle around point, (m, t), M , etc.
Line of best fit drawn on scatter diagram. (A1)(ft)(A1)(ft)
Notes:Award (A1)(ft) for straight line through their mean point, (A1)(ft) for line of best fit with intercept 9(±2) . The second (A1)(ft) can be awarded even if the line does not reach the t-axis but, if extended, the t-intercept is correct.
75 (M1)(A1)(ft)(G2)
Notes: Accept 74.77 from the regression line equation. Award (M1) for indication of the use of their graph to get an estimate OR for correct substitution of 1.7 in the correct regression line equation t = 38.5m + 9.32.
0.960 (0.959614…) (G2)
Note: Award (G0)(G1)(ft) for 0.95, 0.959
Strong and positive (A1)(ft)(A1)(ft)
Note: Follow through from their correlation coefficient in part (f).
(i) Cooking time is much larger (or smaller) than the other eight (A1)
(ii) The gradient of the new line of best fit will be larger (or smaller) (A1)
Note: Some acceptable explanations may include but are not limited to:
The line of best fit may be further away from the plotted points
It may be steeper than the previous line (as the mean would change)
The t-intercept of the new line is smaller (larger)
Do not accept vague explanations, like:
The new line would vary
It would not go through all points
It would not fit the patterns
The line may be slightly tilted
