Question
The function f is defined by \(f(x) = \frac{2}{x} + 3x^2 – 3, x \neq 0\).
(a) Find f'(x)
(b) Find the equation of the normal to the curve y = f(x) at (1, 2) in the form ax + by + d = 0, where \(a, b, d\epsilon \mathbb{Z}\).
Answer/Explanation
Ans:
(a) \(f'(x) = -2x^{-2}+6x\) OR \(f'(x) = -\frac{2}{x^2}+6x\)
(b) finding gradient at x = 1
\(\left.\begin{matrix}
\frac{dy}{dx}
\end{matrix}\right|_{x=1}=4\)
finding the perpendicular gradient
\(m_{\perp} = -\frac{1}{4}\)
\(2=-\frac{1}{4}(1)+c\) OR \(y-2 = -\frac{1}{4}(x-1)\)
x + 4y – 9 = 0
Question
The figure below shows the graphs of functions \(f_1 (x) = x\) and \(f_2 (x) = 5 – x^2\).
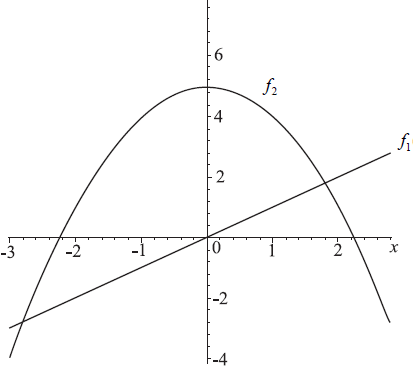
(i) Differentiate \(f_1 (x) \) with respect to x.
(ii) Differentiate \(f_2 (x) \) with respect to x.[3]
Calculate the value of x for which the gradient of the two graphs is the same.[2]
Draw the tangent to the curved graph for this value of x on the figure, showing clearly the property in part (b).[1]
Answer/Explanation
Markscheme
(i) \(f_1 ‘ (x) = 1\) (A1)
(ii) \(f_2 ‘ (x) = – 2x\) (A1)(A1)
(A1) for correct differentiation of each term. (C3)[3 marks]
\(1 = – 2x\) (M1)
\(x = – \frac{1}{2}\) (A1)(ft) (C2)[2 marks]
(A1) is for the tangent drawn at \(x = \frac{1}{2}\) and reasonably parallel to the line \(f_1\) as shown.
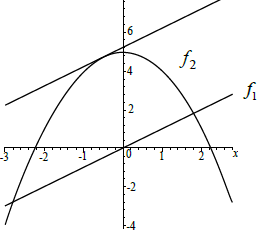(A1) (C1)[1 mark]
Question
Consider the function \(f(x) = 2{x^3} – 5{x^2} + 3x + 1\).
Find \(f'(x)\).[3]
Write down the value of \(f'(2)\).[1]
Find the equation of the tangent to the curve of \(y = f(x)\) at the point \((2{\text{, }}3)\).[2]
Answer/Explanation
Markscheme
\(f'(x) = 6{x^2} – 10x + 3\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for each correct term and no extra terms.
Award (A1)(A1)(A0) if each term correct and extra term seen.
Award(A1)(A0)(A0) if two terms correct and extra term seen.
Award (A0) otherwise.[3 marks]
\(f'(2) = 7\) (A1)(ft) (C1)[1 mark]
\(y = 7x – 11\) or equivalent (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) on their (b) for \(7x\) (must have \(x\)), (A1)(ft) for \( – 11\). Accept \(y – 3 = 7(x – 2)\) .[2 marks]
Question
Consider the function \(f(x) = \frac{1}{2}{x^3} – 2{x^2} + 3\).
Find \(f'(x)\).[2]
Find \(f”(x)\).[2]
Find the equation of the tangent to the curve of \(f\) at the point \((1{\text{, }}1.5)\).[2]
Answer/Explanation
Markscheme
\(\frac{{3{x^2}}}{2} – 4x\) (A1)(A1) (C2)
Note: Award (A1) for each correct term and no extra terms; award (A1)(A0) for both terms correct and extra terms; (A0) otherwise.[2 marks]
\(3x – 4\) (A1)(ft)(A1)(ft) (C2)
Note: accept \(3{x^1} – {4^0}\)[2 marks]
\(y = – 2.5x + 4\) or equivalent (A1)(ft)(A1) (C2)
Note: Award (A1)(ft) on their (a) for \( – 2.5x\) (must have \(x\)), (A1) for \(4\) or equivalent correct answer only.
Accept \(y – 1.5 = – 2.5(x – 1)\)[2 marks]
Question
The function \(f(x)\) is such that \(f'(x) < 0\) for \(1 < x < 4\). At the point \({\text{P}}(4{\text{, }}2)\) on the graph of \(f(x)\) the gradient is zero.
Write down the equation of the tangent to the graph of \(f(x)\) at \({\text{P}}\).[2]
State whether \(f(4)\) is greater than, equal to or less than \(f(2)\).[2]
Given that \(f(x)\) is increasing for \(4 \leqslant x < 7\), what can you say about the point \({\text{P}}\)?[2]
Answer/Explanation
Markscheme
\(y = 2\). (A1)(A1) (C2)
Note: Award (A1) for \(y = \ldots \), (A1) for \(2\).
Accept \(f(x) = 2\) and \(y = 0x + 2\)
Less (than). (A2) (C2)[2 marks]
Local minimum (accept minimum, smallest or equivalent) (A2) (C2)
Note: Award (A1) for stationary or turning point mentioned.
No mark is awarded for \({\text{gradient}} = 0\) as this is given in the question.