Question 13. [Maximum mark: 8]
Sieun hits golf balls into the air. Each time she hits a ball she records θ , the angle at which the ball is launched into the air, and l , the horizontal distance, in metres, which the ball travels
from the point of contact to the first time it lands. The diagram below represents this information.
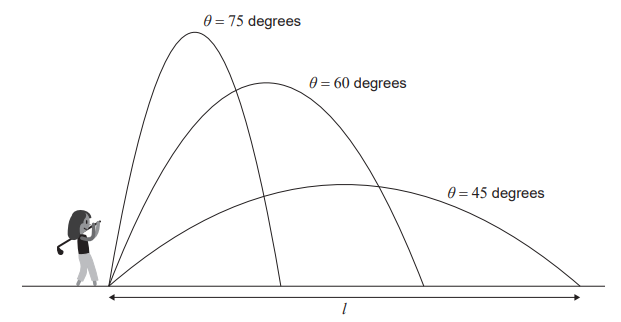
Sieun analyses her results and concludes:
\(\frac{dl}{d\Theta }=-0.2\Theta +9 , 35^{\circ}\leq \Theta \leq 75^{\circ}\)
(a)Determine whether the graph of l against θ is increasing or decreasing at θ = 50° . [3]
(b)Sieun observes that when the angle is 40°, the ball will travel a horizontal distance of 205.5 m.
(c)Find an expression for the function l (θ ) . [5]
▶️Answer/Explanation
(a) \({I}′(50) = – 0.2 × 50 – 9\)
\(= −1 \)
the curve is decreasing at θ = 50°
(b) recognition of need to integrate (e.g. reverse power rule or integral symbol or integrating at least one term correctly)
\(l(\Theta )= -0.1\Theta ^{2}+ 9 \Theta +c\)
\(205.5=-0.1\times (40)^{2}+ 9\times (40)+c \)
\(c= 5.5 \)
\(l(\Theta )=-1.10+ 9\Theta +5.5\)
Question
The cross-section of a beach is modelled by the equation \(y = 0.02x^2\) for \(0 \leq x \leq 10\) where y is the height of the beach (in metres) at a horizontal distance x metres form an origin.
t is the time in hours after low tide.
At t=0 the water is at point (0,0). The height of the water rises at a rate of 0.2 metres per hour. The point W(x(t), y(t)) indicates where the water level meets the beach at time t.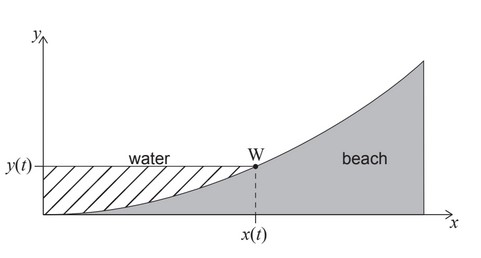
(a) When W has an x-coordinate equal to 1, find the horizontal component of the velocity
of W.
A snail is modelled as a single point. At t = 0 it is positioned at (1 , 0.02). The snail travels
away from the incoming water at a speed of 1 metre per hour in the direction along the curve
of the cross-section of the beach. The following diagram shows this for a value of t, such
that t > 0.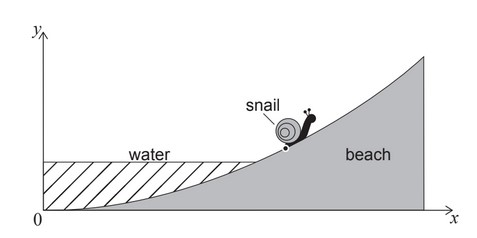
(b) (i) Find the time taken for the snail to reach the point (10 , 2).
(ii) Hence show that the snail reaches the point (10 , 2) before the water does.
▶️Answer/Explanation
Ans:
(a) use of chain rule
\(\frac{dy}{dt} = \frac{dy}{dx} \frac{dx}{dt}\)
attempt to find \(\frac{dy}{dx}\) at x = 1
\(0.2 = 0.04 \times \frac{dx}{dt}\)
\((\frac{dx}{dt}=)\) = 5 \(mh^{-1}\)
(b) (i) if the position of the snail is (X, Y)
from part (a) \(\frac{dX}{dt} = \frac{1}{0.04X}\frac{dY}{dt}\)
since speed is 1:
finding modulus of velocity vector and equating to 1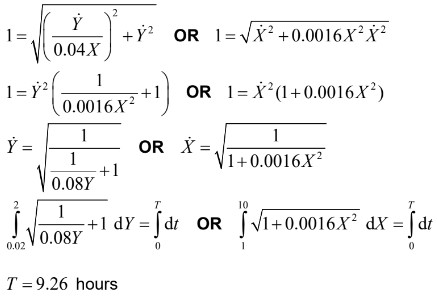
(ii) EITHER
time for water to reach top is \(\frac{0}{0.2}=10\) hours (seen anywhere)
OR
or at time t = 9.26, height of water is \(0.2 \times 9.26 = 1.852\)
THEN
so the water will not reach the snail
Question
A company’s profit per year was found to be changing at a rate of
\(\frac{dP}{dt}=3t^2-8t\)
where P is the company’s profit in thousands of dollars and t is the time since the company
was founded, measured in years.
(a) Determine whether the profit is increasing or decreasing when t = 2.
One year after the company was founded, the profit was 4 thousand dollars.
(b) Find an expression for P(t), when t ≥ 0.
▶️Answer/Explanation
Ans:
(a) METHOD 1
(when t = 2)
\(\frac{dP}{dt} = -4 \) OR \(\frac{dP}{dt}<0\) (equivalent in words) OR \(3(2)^2-8(2)=-4\)
therefore P is decreasing
METHOD 2
sketch with t = 2 indicated in 4th quadrant OR t-intercepts identified
therefore P is decreasing
(b) \((P(t)=)t^3 – 4t^2 (+c)\)
\(4=1^3 – 4(1)^2 + c\)
c =7
\(P(t) = t^3 – 4t^2 + 7\)
Question
. The height of a baseball after it is hit by a bat is modelled by the function
\(h(t) = -4.8t^2 + 21t + 1.2\)
where h(t) is the height in metres above the ground and t is the time in seconds after the ball was hit.
(a) Write down the height of the ball above the ground at the instant it is hit by the bat.
(b) Find the value of t when the ball hits the ground.
(c) State an appropriate domain for t in this model.
▶️Answer/Explanation
Ans:
(a) 1.2 metres
(b) \(-4.8t^2 + 21t + 1.2 = 0\)
(t=) 4.43s (4.431415…s)
(c) \(0 \leq t \leq 4.43\) OR [0, 4.43]
Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
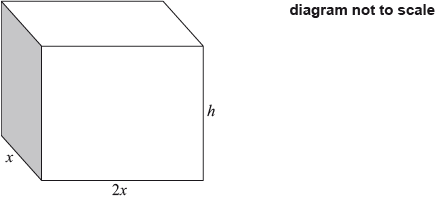
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} – 6{x^3}\).
a.Find the value of \(a\).[3]
b.Find the value of \(x\) that makes the volume a maximum.[3]
▶️Answer/Explanation
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 – 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x – 18{x^2}\) (A1)
\(72x – 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( – 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).