[Maximum mark: 18]
Question:
In the following Argand diagram, the points Z1 , O and Z2 are the vertices of triangle Z1OZ2 described anticlockwise.
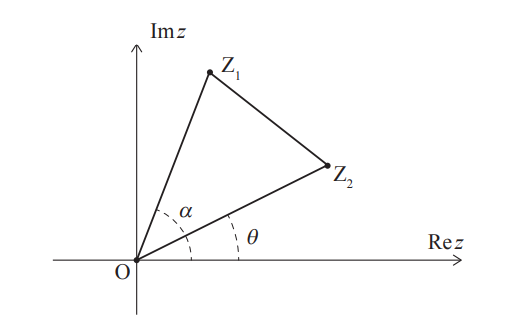
The point Z1 represents the complex number z1 = r1eiα , where r1 > 0. The point Z2 represents the complex number z2 = r2eiθ , where r2 > 0.
Angles α, θ are measured anticlockwise from the positive direction of the real axis such that 0 ≤ α, θ < 2π and 0 < α – θ < π.
(a) Show that z1z2 * = r1r2e i(α – θ) where z2* is the complex conjugate of z2 .
▶️Answer/Explanation
Ans: 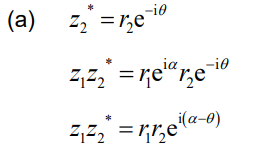
Note: Accept working in modulus-argument form
(b) Given that Re (z1 z2*) = 0, show that Z1OZ2 is a right-angled triangle.
In parts (c), (d) and (e), consider the case where Z1OZ2 is an equilateral triangle.
▶️Answer/Explanation
Ans: 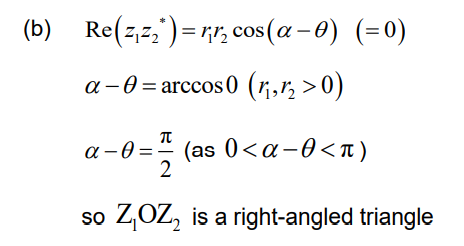
(c) (i) Express z1 in terms of z2 .
▶️Answer/Explanation
Ans: 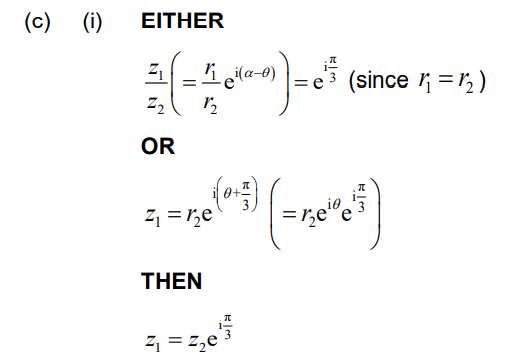
Note: Accept working in either modulus-argument form to obtain \(z_{1} = z_{2}\left ( cos\frac{\pi }{3} + isin\frac{\pi }{3} \right )\) or in Cartesian form to obtain \(z_{1} = z_{2}\left ( \frac{1}{2} + \frac{\sqrt{3}}{2} \right )i\)
(ii) Hence show that z12 + z22 = z1 z2 .
Let z1 and z2 be the distinct roots of the equation z2 + az + b = 0 where z ∈ C and a , b ∈ R.
▶️Answer/Explanation
Ans: 

(d) Use the result from part (c)(ii) to show that a2 – 3b = 0.
Consider the equation z2 + az + 12 = 0, where z ∈ C and a ∈ R.
▶️Answer/Explanation
Ans: 

(e) Given that 0 < α – θ < π, deduce that only one equilateral triangle Z1OZ2 can be formed from the point O and the roots of this equation.
▶️Answer/Explanation
Ans:
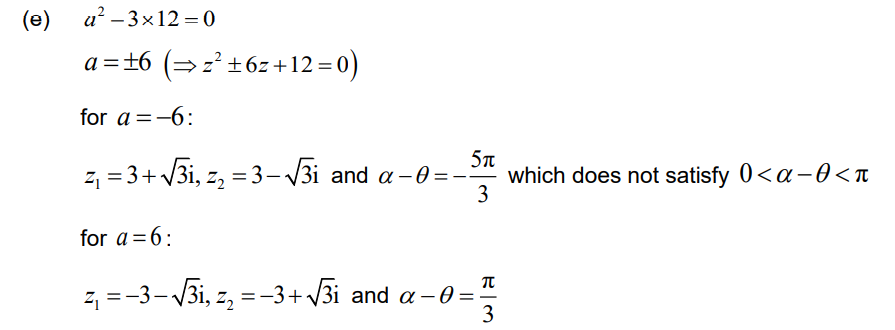
so (for 0 < α – θ < π), only one equilateral triangle can be formed from point O and the two roots of this equation
[Maximum mark: 6]
Question:
Consider the complex numbers z1 = 1 + bi and z2 = (1 – b2) – 2bi, where b ∈ R, b ≠ 0.
(a) Find an expression for z1z2 in terms of b.
▶️Answer/Explanation
Ans: z1z2 = (1 + bi) ((1-b2) – (2b)i)
= (1-b2 – 2i2b2) + i (-2b + b – b3)
= (1 + b2) + i (-b – b3)
Note: Award A1 for 1+ b2 and A1 for − bi – b3i .
(b) Hence, given that arg (z1 z2) = \(\frac{\pi }{4}\) , find the value of b.
▶️Answer/Explanation
Ans: arg (z1z2) = arctan \(\left ( \frac{-b-b^{3}}{1 + b^{2}} \right )= \frac{\pi }{4}\)
EITHER
arctan (-b) = \(\frac{\pi }{4}\) (since 1+b2 ≠, 0 for b ∈ R)
OR
-b – b3 = 1 + b2 (or equivalent)
THEN
b =−1
Question
Consider \(w = 2\left( {{\text{cos}}\frac{\pi }{3} + {\text{i}}\,{\text{sin}}\frac{\pi }{3}} \right)\)
a. These four points form the vertices of a quadrilateral, Q.
i. Express w2 and w3 in modulus-argument form.[3]
▶️Answer/Explanation
Ans: \({w^2} = 4\text{cis}\left( {\frac{{2\pi }}{3}} \right){\text{;}}\,\,{w^3} = 8{\text{cis}}\left( \pi \right)\) (M1)A1A1
Note: Accept Euler form.
Note: M1 can be awarded for either both correct moduli or both correct arguments.
Note: Allow multiplication of correct Cartesian form for M1, final answers must be in modulus-argument form.
[3 marks]
▶️Answer/Explanation
Ans:
A1A1
[2 marks]
▶️Answer/Explanation
Ans:
use of area = \(\frac{1}{2}ab\,\,{\text{sin}}\,C\) M1
\(\frac{1}{2} \times 1 \times 2 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 2 \times 4 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 4 \times 8 \times {\text{sin}}\frac{\pi }{3}\) A1A1
Note: Award A1 for \(C = \frac{\pi }{3}\), A1 for correct moduli.
\( = \frac{{21\sqrt 3 }}{2}\) AG
Note: Other methods of splitting the area may receive full marks.
[3 marks]
Let \(z = 2\left( {{\text{cos}}\frac{\pi }{n} + {\text{i}}\,{\text{sin}}\frac{\pi }{n}} \right),\,\,n \in {\mathbb{Z}^ + }\). The points represented on an Argand diagram by \({z^0},\,\,{z^1},\,\,{z^2},\, \ldots \,,\,\,{z^n}\) form the vertices of a polygon \({P_n}\).
▶️Answer/Explanation
Ans:
\(\frac{1}{2} \times {2^0} \times {2^1} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^1} \times {2^2} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^2} \times {2^3} \times {\text{sin}}\frac{\pi }{n} + \, \ldots \, + \frac{1}{2} \times {2^{n – 1}} \times {2^n} \times {\text{sin}}\frac{\pi }{n}\) M1A1
Note: Award M1 for powers of 2, A1 for any correct expression including both the first and last term.
\( = {\text{sin}}\frac{\pi }{n} \times \left( {{2^0} + {2^2} + {2^4} + \, \ldots \, + {2^{n – 2}}} \right)\)
identifying a geometric series with common ratio 22(= 4) (M1)A1
\( = \frac{{1 – {2^{2n}}}}{{1 – 4}} \times {\text{sin}}\frac{\pi }{n}\) M1
Note: Award M1 for use of formula for sum of geometric series.
\( = \frac{1}{3}\left( {{4^n} – 1} \right){\text{sin}}\frac{\pi }{n}\) A1
[6 marks]
Question
If \({z_1} = a + a\sqrt 3 i\) and \({z_2} = 1 – i\), where a is a real constant, express \({z_1}\) and \({z_2}\) in the form \(r\,{\text{cis}}\,\theta \), and hence find an expression for \({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6}\) in terms of a and i.
▶️Answer/Explanation
Markscheme
\({z_1} = 2a{\text{cis}}\left( {\frac{\pi }{3}} \right){\text{, }}{z_2} = \sqrt 2 {\text{ cis}}\left( { – \frac{\pi }{4}} \right)\) M1 A1 A1
EITHER
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = \frac{{{2^6}{a^6}{\text{cis(0)}}}}{{{{\sqrt 2 }^6}{\text{cis}}\left( {\frac{\pi }{2}} \right)}}\left( { = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)} \right)\) M1 A1 A1
OR
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = {\left( {\frac{{2a}}{{\sqrt 2 }}{\text{cis}}\left( {\frac{{7\pi }}{{12}}} \right)} \right)^6}\) M1 A1
\( = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)\) A1
THEN
\( = – 8{a^6}{\text{i}}\) A1
Note: Accept equivalent angles, in radians or degrees.
Accept alternate answers without cis e.g. \({\text{ = }}\frac{{8{a^6}}}{{\text{i}}}\)
[7 marks]
Question
Given the complex numbers \({z_1} = 1 + 3{\text{i}}\) and \({z_2} = – 1 – {\text{i}}\).
a.Write down the exact values of \(\left| {{z_1}} \right|\) and \(\arg ({z_2})\).[2]
▶️Answer/Explanation
Ans:
\(\left| {{z_1}} \right| = \sqrt {10} ;{\text{ }}\arg ({z_2}) = – \frac{{3\pi }}{4}{\text{ }}\left( {{\text{accept }}\frac{{5\pi }}{4}} \right)\) A1A1
[2 marks]
▶️Answer/Explanation
Ans:
\(\left| {{z_1} + \alpha{z_2}} \right| = \sqrt {{{(1 – \alpha )}^2} + {{(3 – \alpha )}^2}} \) or the squared modulus (M1)(A1)
attempt to minimise \(2{\alpha ^2} – 8\alpha + 10\) or their quadratic or its half or its square root M1
obtain \(\alpha = 2\) at minimum (A1)
state \(\sqrt 2 \) as final answer A1
[5 marks]
Question
(a) Find the polar form of the complex numbers
\(z=1+i\sqrt{3}\) \(w=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i\) \(u=-2\sqrt{3}+2i\)
▶️Answer/Explanation
Ans: \(z=2\left ( cos\frac{\pi }{3}+i\;sin\frac{\pi }3{} \right )\) \(w=cos\left ( -\frac{\pi }{4}\right )+i\;sin\left ( -\frac{\pi }{4} \right )\) \( u=4\left ( cos\frac{5\pi }{6}+i\;sin\frac{5\pi }{6}\right )\)
(b) Then find the polar form of
(i) \( zw\) (ii)\(\frac{z}{w}\) (iii) u3 (iv) \(\frac{z^{2}w^{4}}{u^{3}}\)
▶️Answer/Explanation
Ans: (i) \(zw=2\left ( cos\frac{\pi }{12}+i\;sin\frac{\pi }{12}\right )\) (ii) \(\frac{z}{w}=2\left ( cos\frac{7\pi }{12}+i\;sin\frac{7\pi }{12} \right )\)
(iii) \(u^{3}=64\left ( cos\frac{5\pi }{2}+i\;sin\frac{5\pi }{2} \right )\) (iv) \(\frac{z^{2}w^{4}}{u^{3}}=\frac{1}{16}\left ( cos\left ( -\frac{5\pi }{6} \right )+i\;sin\left ( -\frac{5\pi }{6} \right ) \right )\)
Question
Consider \(w = 2\left( {{\text{cos}}\frac{\pi }{3} + {\text{i}}\,{\text{sin}}\frac{\pi }{3}} \right)\)
a. These four points form the vertices of a quadrilateral, Q.
i.Express w2 and w3 in modulus-argument form.[3]
▶️Answer/Explanation
Ans:
\({w^2} = 4\text{cis}\left( {\frac{{2\pi }}{3}} \right){\text{;}}\,\,{w^3} = 8{\text{cis}}\left( \pi \right)\) (M1)A1A1
Note: Accept Euler form.
Note: M1 can be awarded for either both correct moduli or both correct arguments.
Note: Allow multiplication of correct Cartesian form for M1, final answers must be in modulus-argument form.
[3 marks]
▶️Answer/Explanation
Ans:
A1A1
[2 marks]
▶️Answer/Explanation
Ans: use of area = \(\frac{1}{2}ab\,\,{\text{sin}}\,C\) M1
\(\frac{1}{2} \times 1 \times 2 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 2 \times 4 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 4 \times 8 \times {\text{sin}}\frac{\pi }{3}\) A1A1
Note: Award A1 for \(C = \frac{\pi }{3}\), A1 for correct moduli.
\( = \frac{{21\sqrt 3 }}{2}\) AG
Note: Other methods of splitting the area may receive full marks.
[3 marks]
Let \(z = 2\left( {{\text{cos}}\frac{\pi }{n} + {\text{i}}\,{\text{sin}}\frac{\pi }{n}} \right),\,\,n \in {\mathbb{Z}^ + }\). The points represented on an Argand diagram by \({z^0},\,\,{z^1},\,\,{z^2},\, \ldots \,,\,\,{z^n}\) form the vertices of a polygon \({P_n}\).
▶️Answer/Explanation
Ans:
\(\frac{1}{2} \times {2^0} \times {2^1} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^1} \times {2^2} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^2} \times {2^3} \times {\text{sin}}\frac{\pi }{n} + \, \ldots \, + \frac{1}{2} \times {2^{n – 1}} \times {2^n} \times {\text{sin}}\frac{\pi }{n}\) M1A1
Note: Award M1 for powers of 2, A1 for any correct expression including both the first and last term.
\( = {\text{sin}}\frac{\pi }{n} \times \left( {{2^0} + {2^2} + {2^4} + \, \ldots \, + {2^{n – 2}}} \right)\)
identifying a geometric series with common ratio 22(= 4) (M1)A1
\( = \frac{{1 – {2^{2n}}}}{{1 – 4}} \times {\text{sin}}\frac{\pi }{n}\) M1
Note: Award M1 for use of formula for sum of geometric series.
\( = \frac{1}{3}\left( {{4^n} – 1} \right){\text{sin}}\frac{\pi }{n}\) A1
[6 marks]
Question
If \({z_1} = a + a\sqrt 3 i\) and \({z_2} = 1 – i\), where a is a real constant, express \({z_1}\) and \({z_2}\) in the form \(r\,{\text{cis}}\,\theta \), and hence find an expression for \({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6}\) in terms of a and i.
▶️Answer/Explanation
Markscheme
\({z_1} = 2a{\text{cis}}\left( {\frac{\pi }{3}} \right){\text{, }}{z_2} = \sqrt 2 {\text{ cis}}\left( { – \frac{\pi }{4}} \right)\) M1 A1 A1
EITHER
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = \frac{{{2^6}{a^6}{\text{cis(0)}}}}{{{{\sqrt 2 }^6}{\text{cis}}\left( {\frac{\pi }{2}} \right)}}\left( { = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)} \right)\) M1 A1 A1
OR
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = {\left( {\frac{{2a}}{{\sqrt 2 }}{\text{cis}}\left( {\frac{{7\pi }}{{12}}} \right)} \right)^6}\) M1 A1
\( = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)\) A1
THEN
\( = – 8{a^6}{\text{i}}\) A1
Note: Accept equivalent angles, in radians or degrees.
Accept alternate answers without cis e.g. \({\text{ = }}\frac{{8{a^6}}}{{\text{i}}}\)
[7 marks]
Question
Given the complex numbers \({z_1} = 1 + 3{\text{i}}\) and \({z_2} = – 1 – {\text{i}}\).
a.Write down the exact values of \(\left| {{z_1}} \right|\) and \(\arg ({z_2})\).[2]
▶️Answer/Explanation
Ans: \(\left| {{z_1}} \right| = \sqrt {10} ;{\text{ }}\arg ({z_2}) = – \frac{{3\pi }}{4}{\text{ }}\left( {{\text{accept }}\frac{{5\pi }}{4}} \right)\) A1A1
[2 marks]
b. Find the minimum value of \(\left| {{z_1} + \alpha{z_2}} \right|\), where \(\alpha \in \mathbb{R}\).[5]
▶️Answer/Explanation
Ans: \(\left| {{z_1} + \alpha{z_2}} \right| = \sqrt {{{(1 – \alpha )}^2} + {{(3 – \alpha )}^2}} \) or the squared modulus (M1)(A1)
attempt to minimise \(2{\alpha ^2} – 8\alpha + 10\) or their quadratic or its half or its square root M1
obtain \(\alpha = 2\) at minimum (A1)
state \(\sqrt 2 \) as final answer A1
[5 marks]
Question
(a) Find the polar form of the complex numbers
\(z=1+i\sqrt{3}\) \(w=\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i\) \(u=-2\sqrt{3}+2i\)
▶️Answer/Explanation
Ans: \(z=2\left ( cos\frac{\pi }{3}+i\;sin\frac{\pi }3{} \right )\) \(w=cos\left ( -\frac{\pi }{4}\right )+i\;sin\left ( -\frac{\pi }{4} \right )\) \( u=4\left ( cos\frac{5\pi }{6}+i\;sin\frac{5\pi }{6}\right )\)
(b) Then find the polar form of
(i) \( zw\) (ii)\(\frac{z}{w}\) (iii) u3 (iv) \(\frac{z^{2}w^{4}}{u^{3}}\)
▶️Answer/Explanation
Ans: (i) \(zw=2\left ( cos\frac{\pi }{12}+i\;sin\frac{\pi }{12}\right )\) (ii) \(\frac{z}{w}=2\left ( cos\frac{7\pi }{12}+i\;sin\frac{7\pi }{12} \right )\)
(iii) \(u^{3}=64\left ( cos\frac{5\pi }{2}+i\;sin\frac{5\pi }{2} \right )\) (iv) \(\frac{z^{2}w^{4}}{u^{3}}=\frac{1}{16}\left ( cos\left ( -\frac{5\pi }{6} \right )+i\;sin\left ( -\frac{5\pi }{6} \right ) \right )\)
