Question
A sector of a circle, centre O and radius 4.5m, is shown in the following diagram.
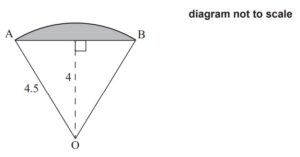
(a) (i) Find the angle AÔB.
(ii) Find the area of the shaded segment. [8]
A square field with side 8m has a goat tied to a post in the centre by a rope such that the
goat can reach all parts of the field up to 4.5m from the post.
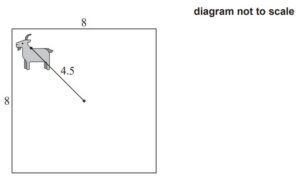
(b) (i) Find the area of a circle with radius 4.5m.
(ii) Find the area of the field that can be reached by the goat. [5]
Let V be the volume of grass eaten by the goat, in cubic metres, and t be the length of time,
in hours, that the goat has been in the field.
The goat eats grass at the rate of \(\frac{dV}{dt}=0.3te^{-t}\).
(c) Find the value of t at which the goat is eating grass at the greatest rate. [2]
Answer/Explanation
Ans
4. (a) (i) \(\left ( \frac{1}{2}A\hat{O}B= \right )\arccos \left ( \frac{4}{4.5} \right )=27.266…\) (M1)(A1)
AOB 54.532… ≈ 54.5 o = ( 0.951764…≈ 0.952 radians) A1
Note: Other methods may be seen; award (M1)(A1) for use of a correct trigonometric
method to find an appropriate angle and then A1 for the correct answer.
(ii) finding area of triangle
EITHER
area of triangle \(=\frac{1}{2}\times 4.5^{2}\times \sin (54.532…)\) (M1)
Note: Award M1 for correct substitution into formula.
= 8.24621…≈ 8.25 m2
OR
\(AB=2\times \sqrt{4.5^{2}-4^{2}}=4.1231…\) (M1)
\(area\ triangle=\frac{4.12131…\times 4}{2}\) (A1)
= 8.24621…≈ 8.25 m2
EITHER
\(area\ of \ sector=\frac{54.532…}{360}\times \pi \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2
OR
\(area\ of \ sector=\frac{1}{2}\times 0.9517641.. \times 4.5^{2}\) (M1)
= 9.63661… ≈ 9.64 m2 (A1)
THEN
area of segment = 9.63661… 8.24621… −
=1.39 m2 (1.39040…) A1
[8 marks]
(b) (i) 2 π× 4.5 (M1)
63.6 m2 (63.6172… m2 ) A1
(ii) METHOD 1
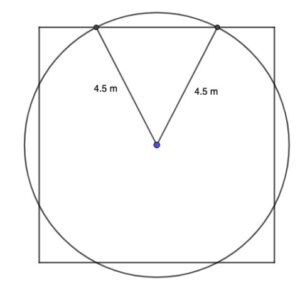
4 1.39040… × (5.56160) (A1)
subtraction of four segments from area of circle (M1)
= 58.1 m2 (58.055…) A1
METHOD 2
\(4(0.5\times 4.5^{2} \times\sin 54.532… )+4\left ( \frac{35.4679}{360}\times\pi \times 4.5^{2} \right )\) (M1)
= 32.9845… + 25.0707 (A1)
= 58.1 m2 (58.055 …) A1
[5 marks]
(c) sketch of \(\frac{dV}{dt}\) OR \(\frac{dV}{dt}=0.110363…\) OR attempt to find where \(\frac{d^{2}V}{dt^{2}}=0\) (M1)
t =1 hour A1
[2 marks]
[Total 15 marks]
Question
Consider the function f (x) = x3 – 3x– 24x + 30.
Write down f (0).[1]
Find \(f'(x)\).[3]
Find the gradient of the graph of f (x) at the point where x = 1.[2]
(i) Use f ‘(x) to find the x-coordinate of M and of N.
(ii) Hence or otherwise write down the coordinates of M and of N.[5]
Sketch the graph of f (x) for \( – 5 \leqslant x \leqslant 7\) and \( – 60 \leqslant y \leqslant 60\). Mark clearly M and N on your graph.[4]
Lines L1 and L2 are parallel, and they are tangents to the graph of f (x) at points A and B respectively. L1 has equation y = 21x + 111.
(i) Find the x-coordinate of A and of B.
(ii) Find the y-coordinate of B.[6]
Answer/Explanation
Markscheme
30 (A1)[1 mark]
f ‘(x) = 3x2 – 6x – 24 (A1)(A1)(A1)
Note: Award (A1) for each term. Award at most (A1)(A1) if extra terms present.[3 marks]
f ‘(1) = –27 (M1)(A1)(ft)(G2)
Note: Award (M1) for substituting x = 1 into their derivative.[2 marks]
(i) f ‘(x) = 0
3x2 – 6x – 24 = 0 (M1)
x = 4; x = –2 (A1)(ft)(A1)(ft)
Notes: Award (M1) for either f ‘(x) = 0 or 3x2 – 6x – 24 = 0 seen. Follow through from their derivative. Do not award the two answer marks if derivative not used.
(ii) M(–2, 58) accept x = –2, y = 58 (A1)(ft)
N(4, – 50) accept x = 4, y = –50 (A1)(ft)
Note: Follow through from their answer to part (d) (i).[5 marks]
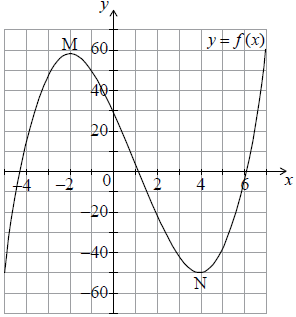
(A1) for window
(A1) for a smooth curve with the correct shape
(A1) for axes intercepts in approximately the correct positions
(A1) for M and N marked on diagram and in approximately
correct position (A4)
Note: If window is not indicated award at most (A0)(A1)(A0)(A1)(ft).[4 marks]
(i) 3x2 – 6x – 24 = 21 (M1)
3x2 – 6x – 45 = 0 (M1)
x = 5; x = –3 (A1)(ft)(A1)(ft)(G3)
Note: Follow through from their derivative.
OR
Award (A1) for L1 drawn tangent to the graph of f on their sketch in approximately the correct position (x = –3), (A1) for a second tangent parallel to their L1, (A1) for x = –3, (A1) for x = 5 . (A1)(ft)(A1)(ft)(A1)(A1)
Note: If only x = –3 is shown without working award (G2). If both answers are shown irrespective of workingaward (G3).
(ii) f (5) = –40 (M1)(A1)(ft)(G2)
Notes: Award (M1) for attempting to find the image of their x = 5. Award (A1) only for (5, –40). Follow through from their x-coordinate of B only if it has been clearly identified in (f) (i).[6 marks]
Question
Consider the function \(f(x) = {x^3} + \frac{{48}}{x}{\text{, }}x \ne 0\).
Calculate \(f(2)\) .[2]
Sketch the graph of the function \(y = f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 200 \leqslant y \leqslant 200\) .[4]
Find \(f'(x)\) .[3]
Find \(f'(2)\) .[2]
Write down the coordinates of the local maximum point on the graph of \(f\) .[2]
Find the gradient of the tangent to the graph of \(f\) at \(x = 1\).[2]
There is a second point on the graph of \(f\) at which the tangent is parallel to the tangent at \(x = 1\).
Find the \(x\)-coordinate of this point.[2]
Answer/Explanation
Markscheme
\(f(2) = {2^3} + \frac{{48}}{2}\) (M1)
\(= 32\) (A1)(G2)[2 marks]
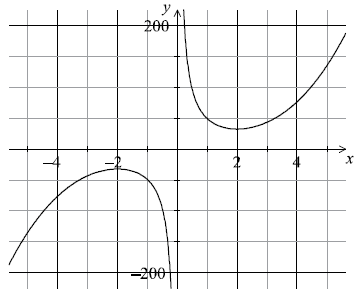
(A1) for labels and some indication of scale in an appropriate window
(A1) for correct shape of the two unconnected and smooth branches
(A1) for maximum and minimum in approximately correct positions
(A1) for asymptotic behaviour at \(y\)-axis (A4)
Notes: Please be rigorous.
The axes need not be drawn with a ruler.
The branches must be smooth: a single continuous line that does not deviate from its proper direction.
The position of the maximum and minimum points must be symmetrical about the origin.
The \(y\)-axis must be an asymptote for both branches. Neither branch should touch the axis nor must the curve approach the
asymptote then deviate away later.[4 marks]
\(f'(x) = 3{x^2} – \frac{{48}}{{{x^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(3{x^2}\) , (A1) for \( – 48\) , (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(2) = 3{(2)^2} – \frac{{48}}{{{{(2)}^2}}}\) (M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative.
\(= 0\) (A1)(ft)(G1)[2 marks]
\(( – 2{\text{, }} – 32)\) or \(x = – 2\), \(y = – 32\) (G1)(G1)
Notes: Award (G0)(G0) for \(x = – 32\), \(y = – 2\) . Award at most (G0)(G1) if parentheses are omitted.[2 marks]
\(\{ y \geqslant 32\} \cup \{ y \leqslant – 32\} \) (A1)(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) \(y \geqslant 32\) or \(y > 32\) seen, (A1)(ft) for \(y \leqslant – 32\) or \(y < – 32\) , (A1) for weak (non-strict) inequalities used in both of the above.
Accept use of \(f\) in place of \(y\). Accept alternative interval notation.
Follow through from their (a) and (e).
If domain is given award (A0)(A0)(A0).
Award (A0)(A1)(ft)(A1)(ft) for \([ – 200{\text{, }} – 32]\) , \([32{\text{, }}200]\).
Award (A0)(A1)(ft)(A1)(ft) for \(] – 200{\text{, }} – 32]\) , \([32{\text{, }}200[\).[3 marks]
\(f'(1) = – 45\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for \(f'(1)\) seen or substitution of \(x = 1\) into their derivative. Follow through from their derivative if working is seen.[2 marks]
\(x = – 1\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for equating their derivative to their \( – 45\) or for seeing parallel lines on their graph in the approximately correct position.[2 marks]
Question
Consider the function \(f(x) = – \frac{1}{3}{x^3} + \frac{5}{3}{x^2} – x – 3\).
Sketch the graph of y = f (x) for −3 ≤ x ≤ 6 and −10 ≤ y ≤ 10 showing clearly the axes intercepts and local maximum and minimum points. Use a scale of 2 cm to represent 1 unit on the x-axis, and a scale of 1 cm to represent 1 unit on the y-axis.[4]
Find the value of f (−1).[2]
Write down the coordinates of the y-intercept of the graph of f (x).[1]
Find f ‘(x).[3]
Show that \(f'( – 1) = – \frac{{16}}{3}\).[1]
Explain what f ‘(−1) represents.[2]
Find the equation of the tangent to the graph of f (x) at the point where x is –1.[2]
Sketch the tangent to the graph of f (x) at x = −1 on your diagram for (a).[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Write down the value of
(i) a ;
(ii) b .[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Describe the behaviour of f (x) for a < x < b.[1]
Answer/Explanation
Markscheme
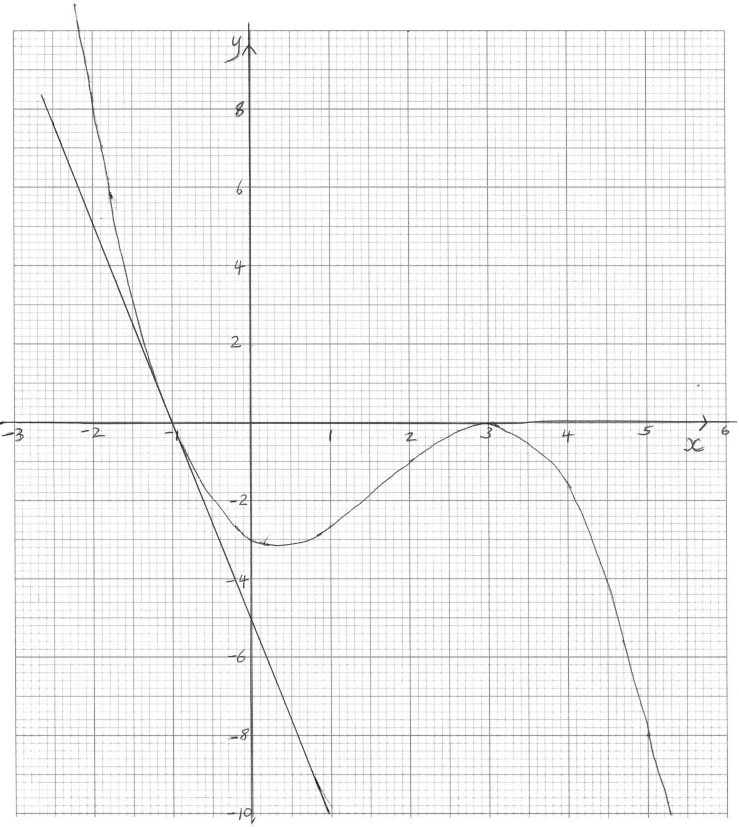
(A1) for indication of window and labels. (A1) for smooth curve that does not enter the first quadrant, the curve must consist of one line only.
(A1) for x and y intercepts in approximately correct positions (allow ±0.5).
(A1) for local maximum and minimum in approximately correct position. (minimum should be 0 ≤ x ≤ 1 and –2 ≤ y ≤ –4 ), the y-coordinate of the maximum should be 0 ± 0.5. (A4)[4 marks]
\(-\frac{1}{3}(-1)^3 + \frac{5}{3}(-1)^2 – (-1) – 3 \) (M1)
Note: Award (M1) for substitution of –1 into f (x)
= 0 (A1)(G2)[2 marks]
(0, –3) (A1)
OR
x = 0, y = –3 (A1)
Note: Award (A0) if brackets are omitted.[1 mark]
\(f'(x) = – {x^2} + \frac{{10}}{3}x – 1\) (A1)(A1)(A1)
Note: Award (A1) for each correct term. Award (A1)(A1)(A0) at most if there are extra terms.[3 marks]
\(f'( – 1) = – {( – 1)^2} + \frac{{10}}{3}( – 1) – 1\) (M1)
\(= -\frac{16}{3}\) (AG)
Note: Award (M1) for substitution of x = –1 into correct derivative only. The final answer must be seen.[1 mark]
f ‘(–1) gives the gradient of the tangent to the curve at the point with x = –1. (A1)(A1)
Note: Award (A1) for “gradient (of curve)”, (A1) for “at the point with x = –1”. Accept “the instantaneous rate of change of y” or “the (first) derivative”.[2 marks]
\(y = – \frac{16}{3} x + c\) (M1)
Note: Award (M1) for \(-\frac{16}{3}\) substituted in equation.
\(0 = – \frac{16}{3} \times (-1) + c \)
\(c = – \frac{16}{3}\)
\(y = – \frac{{16}}{3}x – \frac{{16}}{3}\) (A1)(G2)
Note: Accept y = –5.33x – 5.33.
OR
\((y – 0) = \frac{{-16}}{3}(x + 1)\) (M1)(A1)(G2)
Note: Award (M1) for \( – \frac{{16}}{3}\) substituted in equation, (A1) for correct equation. Follow through from their answer to part (b). Accept y = –5.33 (x +1). Accept equivalent equations.[2 marks]
(A1)(ft) for a tangent to their curve drawn.
(A1)(ft) for their tangent drawn at the point x = –1. (A1)(ft)(A1)(ft)
Note: Follow through from their graph. The tangent must be a straight line otherwise award at most (A0)(A1).[2 marks]
(i) \(a = \frac{1}{3}\) (G1)
(ii) \(b = 3\) (G1)
Note: If a and b are reversed award (A0)(A1).[2 marks]
f (x) is increasing (A1)[1 mark]
Question
Consider the function \(f(x) = \frac{{96}}{{{x^2}}} + kx\), where \(k\) is a constant and \(x \ne 0\).
Write down \(f'(x)\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Show that \(k = 3\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f(2)\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f'(2)\)[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find the equation of the normal to the graph of \(y = f(x)\) at the point where \(x = 2\).
Give your answer in the form \(ax + by + d = 0\) where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Sketch the graph of \(y = f(x)\), for \( – 5 \leqslant x \leqslant 10\) and \( – 10 \leqslant y \leqslant 100\).[4]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Write down the coordinates of the point where the graph of \(y = f(x)\) intersects the \(x\)-axis.[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
State the values of \(x\) for which \(f(x)\) is decreasing.[2]
Answer/Explanation
Markscheme
\(\frac{{ – 192}}{{{x^3}}} + k\) (A1)(A1)(A1)
Note: Award (A1) for \(-192\), (A1) for \({x^{ – 3}}\), (A1) for \(k\) (only).
at local minimum \(f'(x) = 0\) (M1)
Note: Award (M1) for seeing \(f'(x) = 0\) (may be implicit in their working).
\(\frac{{ – 192}}{{{4^3}}} + k = 0\) (A1)
\(k = 3\) (AG)
Note: Award (A1) for substituting \(x = 4\) in their \(f'(x) = 0\), provided it leads to \(k = 3\). The conclusion \(k = 3\) must be seen for the (A1) to be awarded.
\(\frac{{96}}{{{2^2}}} + 3(2)\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in \(f(x)\).
\( = 30\) (A1)(G2)
\(\frac{{ – 192}}{{{2^3}}} + 3\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in their \(f'(x)\).
\( = – 21\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(y – 30 = \frac{1}{{21}}(x – 2)\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \(\frac{1}{{21}}\) seen, (M1) for the correct substitution of their point and their normal gradient in equation of a line.
Follow through from part (c) and part (d).
OR
gradient of normal \( = \frac{1}{{21}}\) (A1)(ft)
\(30 = \frac{1}{{21}} \times 2 + c\) (M1)
\(c = 29\frac{{19}}{{21}}\)
\(y = \frac{1}{{21}}x + 29\frac{{19}}{{21}}\;\;\;(y = 0.0476x + 29.904)\)
\(x – 21y + 628 = 0\) (A1)(ft)(G2)
Notes: Accept equivalent answers.
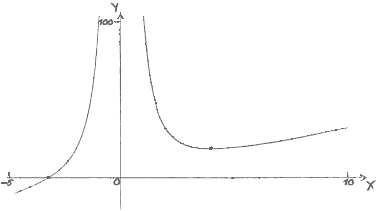(A1)(A1)(A1)(A1)
Notes: Award (A1) for correct window (at least one value, other than zero, labelled on each axis), the axes must also be labelled; (A1) for a smooth curve with the correct shape (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis), on the given domain; (A1) for axis intercept in approximately the correct position (nearer \(-5\) than zero); (A1) for local minimum in approximately the correct position (first quadrant, nearer the \(y\)-axis than \(x = 10\)).
If there is no scale, award a maximum of (A0)(A1)(A0)(A1) – the final (A1) being awarded for the zero and local minimum in approximately correct positions relative to each other.
\(( – 3.17,{\text{ }}0)\;\;\;\left( {( – 3.17480 \ldots ,{\text{ 0)}}} \right)\) (G1)(G1)
Notes: If parentheses are omitted award (G0)(G1)(ft).
Accept \(x = – 3.17,{\text{ }}y = 0\). Award (G1) for \(-3.17\) seen.
\(0 < x \leqslant 4{\text{ or }}0 < x < 4\) (A1)(A1)
Notes: Award (A1) for correct end points of interval, (A1) for correct notation (note: lower inequality must be strict).
Award a maximum of (A1)(A0) if \(y\) or \(f(x)\) used in place of \(x\).