Question
A toy rocket is made from a plastic bottle that contains some water.
Air is pumped into the vertical bottle until the pressure inside forces water and air out of the bottle. The bottle then travels vertically upwards.
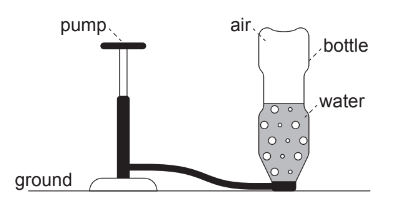
The air–water mixture is called the propellant.
The variation with time of the vertical velocity of the bottle is shown.
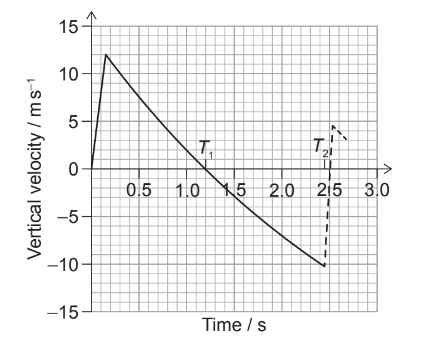
The bottle reaches its highest point at time \(T_1\) on the graph and returns to the ground at time \(T_2\). The bottle then bounces. The motion of the bottle after the bounce is shown as a dashed line.
(a) Estimate, using the graph, the maximum height of the bottle.[3]
(b) Estimate the acceleration of the bottle when it is at its maximum height. [2]
(c) The bottle bounces when it returns to the ground.
(i) Calculate the fraction of the kinetic energy of the bottle that remains after the bounce.
(ii) The mass of the bottle is 27g and it is in contact with the ground for 85ms. Determine the average force exerted by the ground on the bottle. Give your answer to an appropriate number of significant figures. [3]
(d) The maximum height reached by the bottle is greater with an air–water mixture than with only high-pressure air in the bottle.
Assume that the speed at which the propellant leaves the bottle is the same in both cases Explain why the bottle reaches a greater maximum height with an air–water mixture. [2]
▶️Answer/Explanation
Ans:
a. ALTERNATIVE 1
Attempt to count squares \(\checkmark\)
Area of one square found \(\checkmark\)
7.2 «m» (accept \(6.4-7.4 \mathrm{~m}\) )
ALTERNATIVE 2
Uses area equation for either triangle \(\checkmark\)
Correct read offs for estimate of area of triangle
\(7.2 \approx \mathrm{m} »\) (accept \(6.4-7.4\) )
b Attempt to calculate gradient of line at \(t=1.2 \mathrm{~s} \checkmark\)
$
\left.\alpha \rightarrow 9.8 \ll \mathrm{m} \mathrm{s}^{-2} \rightsquigarrow \text { (accept } 9.6-10.0\right) \checkmark
$
c i Attempt to evaluate KE ratio as \(\left(\frac{v_{\text {final }}}{v_{\text {initial }}}\right)^2 \checkmark\)
$
\left(\frac{4.5}{10}\right)^2 \Rightarrow 0.20 \text { OR } 20 \% \text { OR } \frac{1}{5}
$
ii Attempt to use force \(=\) momentum change \(\div\) time \(\checkmark\)
$
\begin{aligned}
& \alpha=\frac{(4.5+10) \times 0.027}{85 \times 10^{-3}}=4.6 » \\
& \text { Force }=\ll 4.6+0.3 » 4.9 \ll \mathrm{N} »
\end{aligned}
$
Any answer to 2 sf \(\checkmark\)
Mass «leaving the bottle per second» will be larger for air-water \(\checkmark\) the momentum change/force is greater \(\checkmark\)
Question
A ball of mass 0.800kg is attached to a string. The distance to the centre of the mass of the ball from the point of support is 95.0cm. The ball is released from rest when the string is horizontal. When the string becomes vertical the ball collides with a block of mass 2.40kg that is at rest on a horizontal surface.
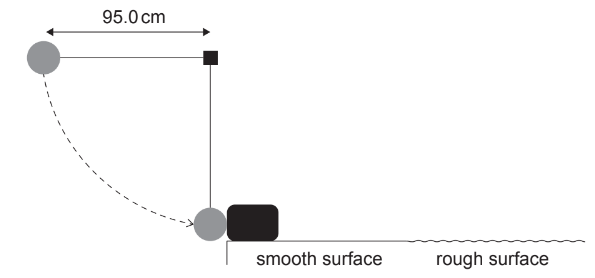
(a) Just before the collision of the ball with the block,
(i) draw a free-body diagram for the ball. [2]
(ii) show that the speed of the ball is about \(4.3 \mathrm{~ms}^{-1}\). [1]
(iii) determine the tension in the string. [2]
(b) After the collision, the ball rebounds and the block moves with speed 2.16ms-1.
(i) Show that the collision is elastic. [4]
(ii) Calculate the maximum height risen by the centre of the ball. [2]
(c) The coefficient of dynamic friction between the block and the rough surface is 0.400.
Estimate the distance travelled by the block on the rough surface until it stops. [3]
▶️Answer/Explanation
Ans:
a(i) Tension upwards, weight downwards \(\checkmark\) Tension is clearly longer than weight \(\checkmark\)
( ii )\(v=\sqrt{2 \times 9.81 \times 0.95}\) OR \(=4.32 \mathrm{kms}^{-1} n\)
iii \(\begin{aligned} & T-m g=F_{\text {net }} O R \quad T-m g=\frac{m v^2}{r} \checkmark \\ & T \ll=0.800 \times 9.81+\frac{0.800 \times 4.317^2}{0.95} \otimes=23.5 \ll \mathrm{Nw}\end{aligned}\)
b i Use of conservation of momentum.
Rebound speed \(=2.16 \propto \mathrm{m} \mathrm{s}^{-1}\) w
Calculation of initial KE \(=* \frac{1}{2} \times 0.800 \times 4.317^2 n=7.46 * \mathrm{~J}\)
Calculation of final KE \(=\propto \frac{1}{2} \times 0.800 \times 2.16^2+\frac{1}{2} \times 2.40 \times 2.16^2 n=7.46 \propto \mathrm{J} »\) shence elastic”
b ii ALTERNATIVE 1
Rebound speed is halved so energy less by a factor of \(4 \checkmark\) Hence height is \(\frac{95}{4}=23.8 \% \mathrm{~cm} \otimes\)
ALTERNATIVE 2
Use of conservation of energy / \(\frac{1}{2} \times 0.800 \times 2.16^2=0.800 \times 9.8 \times h\) OR
Use of proper kinematics equation (e.g. \(0=2.16^2-2 \times 9.8 \times h\) ) \(h=23.8 * \mathrm{~cm} \otimes\)
c.ALTERNATIVE 1
Frictional force is \(f \ll=0.400 \times 2.40 \times 9.81 »=9.42 * N \cdots v\)
\(9.42 \times d=\frac{1}{2} \times 2.40 \times 2.16^2\) OR \(d=\frac{5.5987}{9.42}\)
\(d=0.594 \ll \mathrm{m} » \checkmark\)
ALTERNATIVE 2
$
a=\ll \frac{f}{m}=\mu g=0.4 \times 9.81=» 3.924 \ll \mathrm{m} \mathrm{s}^{-2}{ }_w \checkmark
$
Proper use of kinematics equation(s) to determine
$
d=0.594 \ll \mathrm{m} »
$