Question
A ball of mass 0.800kg is attached to a string. The distance to the centre of the mass of the ball from the point of support is 95.0cm. The ball is released from rest when the string is horizontal. When the string becomes vertical the ball collides with a block of mass 2.40kg that is at rest on a horizontal surface.
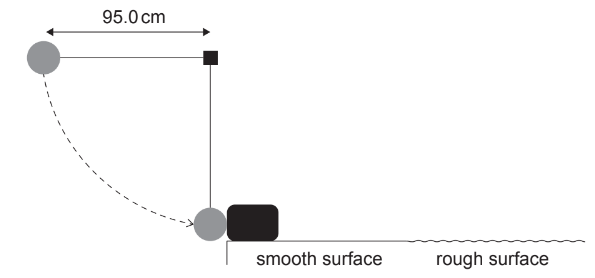
(a) Just before the collision of the ball with the block,
(i) draw a free-body diagram for the ball. [2]
(ii) show that the speed of the ball is about \(4.3 \mathrm{~ms}^{-1}\). [1]
(iii) determine the tension in the string. [2]
(b) After the collision, the ball rebounds and the block moves with speed 2.16ms-1.
(i) Show that the collision is elastic. [4]
(ii) Calculate the maximum height risen by the centre of the ball. [2]
(c) The coefficient of dynamic friction between the block and the rough surface is 0.400.
Estimate the distance travelled by the block on the rough surface until it stops. [3]
▶️Answer/Explanation
Ans:
a(i) Tension upwards, weight downwards \(\checkmark\) Tension is clearly longer than weight \(\checkmark\)
( ii )\(v=\sqrt{2 \times 9.81 \times 0.95}\) OR \(=4.32 \mathrm{kms}^{-1} n\)
iii \(\begin{aligned} & T-m g=F_{\text {net }} O R \quad T-m g=\frac{m v^2}{r} \checkmark \\ & T \ll=0.800 \times 9.81+\frac{0.800 \times 4.317^2}{0.95} \otimes=23.5 \ll \mathrm{Nw}\end{aligned}\)
b i Use of conservation of momentum.
Rebound speed \(=2.16 \propto \mathrm{m} \mathrm{s}^{-1}\) w
Calculation of initial KE \(=* \frac{1}{2} \times 0.800 \times 4.317^2 n=7.46 * \mathrm{~J}\)
Calculation of final KE \(=\propto \frac{1}{2} \times 0.800 \times 2.16^2+\frac{1}{2} \times 2.40 \times 2.16^2 n=7.46 \propto \mathrm{J} »\) shence elastic”
b ii ALTERNATIVE 1
Rebound speed is halved so energy less by a factor of \(4 \checkmark\) Hence height is \(\frac{95}{4}=23.8 \% \mathrm{~cm} \otimes\)
ALTERNATIVE 2
Use of conservation of energy / \(\frac{1}{2} \times 0.800 \times 2.16^2=0.800 \times 9.8 \times h\) OR
Use of proper kinematics equation (e.g. \(0=2.16^2-2 \times 9.8 \times h\) ) \(h=23.8 * \mathrm{~cm} \otimes\)
c.ALTERNATIVE 1
Frictional force is \(f \ll=0.400 \times 2.40 \times 9.81 »=9.42 * N \cdots v\)
\(9.42 \times d=\frac{1}{2} \times 2.40 \times 2.16^2\) OR \(d=\frac{5.5987}{9.42}\)
\(d=0.594 \ll \mathrm{m} » \checkmark\)
ALTERNATIVE 2
$
a=\ll \frac{f}{m}=\mu g=0.4 \times 9.81=» 3.924 \ll \mathrm{m} \mathrm{s}^{-2}{ }_w \checkmark
$
Proper use of kinematics equation(s) to determine
$
d=0.594 \ll \mathrm{m} »
$