Question
A simple pendulum oscillates with frequency \(f\). The length of the pendulum is halved. What is the new frequency of the pendulum?
A. \(2 f\)
B. \(\sqrt{2} f\)
C. \(\frac{f}{\sqrt{2}}\)
D. \(\frac{f}{2}\)
▶️Answer/Explanation
Ans:B
The frequency \(f\) of a simple pendulum is given by the formula:
\[f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}\]
If you halve the length of the pendulum (\(L \rightarrow \frac{L}{2}\)), the new frequency (\(f’\)) can be calculated as:
\[f’ = \frac{1}{2\pi}\sqrt{\frac{g}{\frac{L}{2}}}\]
Simplify the expression:
\[f’ = \frac{1}{2\pi}\sqrt{\frac{2g}{L}}\]
Now, let’s compare \(f\) and \(f’\):
\[\frac{f’}{f} = \frac{\frac{1}{2\pi}\sqrt{\frac{2g}{L}}}{\frac{1}{2\pi}\sqrt{\frac{g}{L}}}\]
Now, simplify further:
\[\frac{f’}{f} = \sqrt{\frac{2g}{L} \cdot \frac{L}{g}}\]
\[\frac{f’}{f} = \sqrt{2}\]
So, the new frequency \(f’\) is \(\sqrt{2}\) times the original frequency \(f\). Therefore, the correct answer is:B.
Question
Which graph represents the variation with displacement of the potential energy \(P\) and the total energy \(T\) of a system undergoing simple harmonic motion (SHM)?
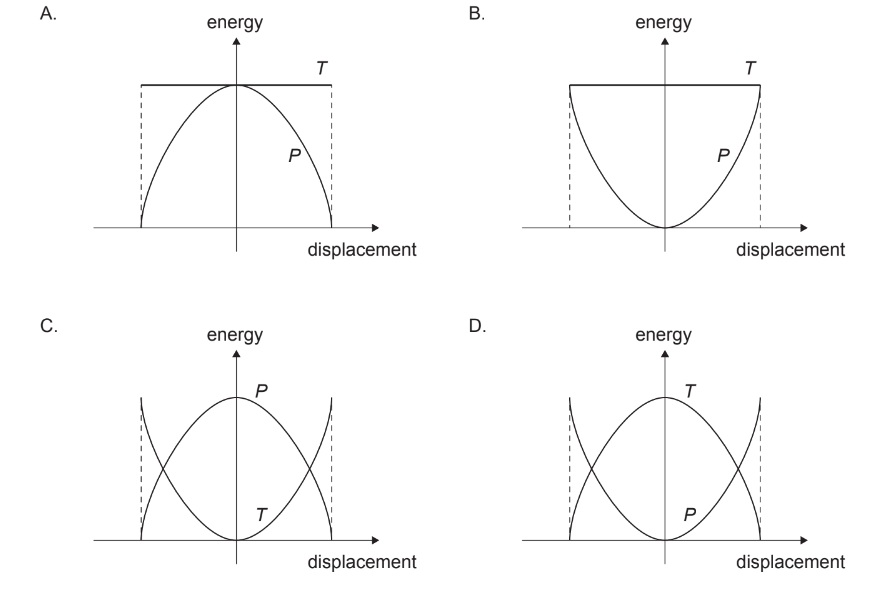
▶️Answer/Explanation
Ans:B

Question
A mass oscillating in simple harmonic motion on the end of a spring has an amplitude \(x_0\) and a total energy \(E_{\mathrm{T}}\). The mass on the spring is doubled and made to oscillate with the same amplitude \(x_0\).
What is the total energy of the oscillating system after the change?
A. \(E_{\mathrm{T}}\)
B. \(\sqrt{2} E_{\mathrm{T}}\)
C. \(2 E_{\mathrm{T}}\)
D. \(4 E_{\mathrm{T}}\)
▶️Answer/Explanation
Ans:A
The total energy \(E_T\) of a simple harmonic oscillator is a constant and is proportional to the square of the amplitude (\(x_0\)) of the oscillation. Therefore, if the amplitude remains the same and only the mass on the spring is doubled, the total energy will also remain the same. This is because the total energy of the system is not dependent on the mass of the object undergoing simple harmonic motion.
A particle performs simple harmonic oscillations. Which of the following quantities will be unaffected by a reduction in the amplitude of oscillations?
A. The total energy
B. The maximum speed
C. The maximum acceleration
D. The period
Answer/Explanation
Answer – D
Total energy \( =\frac{1}{2}KA^{2} \)
\( v_{max}=A\omega \)
\( a_{max}=-A\omega ^{2} \)
Time period \( \left ( T \right )=\frac{2\pi }{\omega } \)
Only time period does not depend on amplitude
Question
A pendulum oscillating near the surface of the Earth swings with a time period T. What is the time period of the same pendulum near the surface of the planet Mercury where the gravitational field strength is 0.4g?
A. 0.4T
B. 0.6T
C. 1.6T
D. 2.5T
Answer/Explanation
Markscheme
C
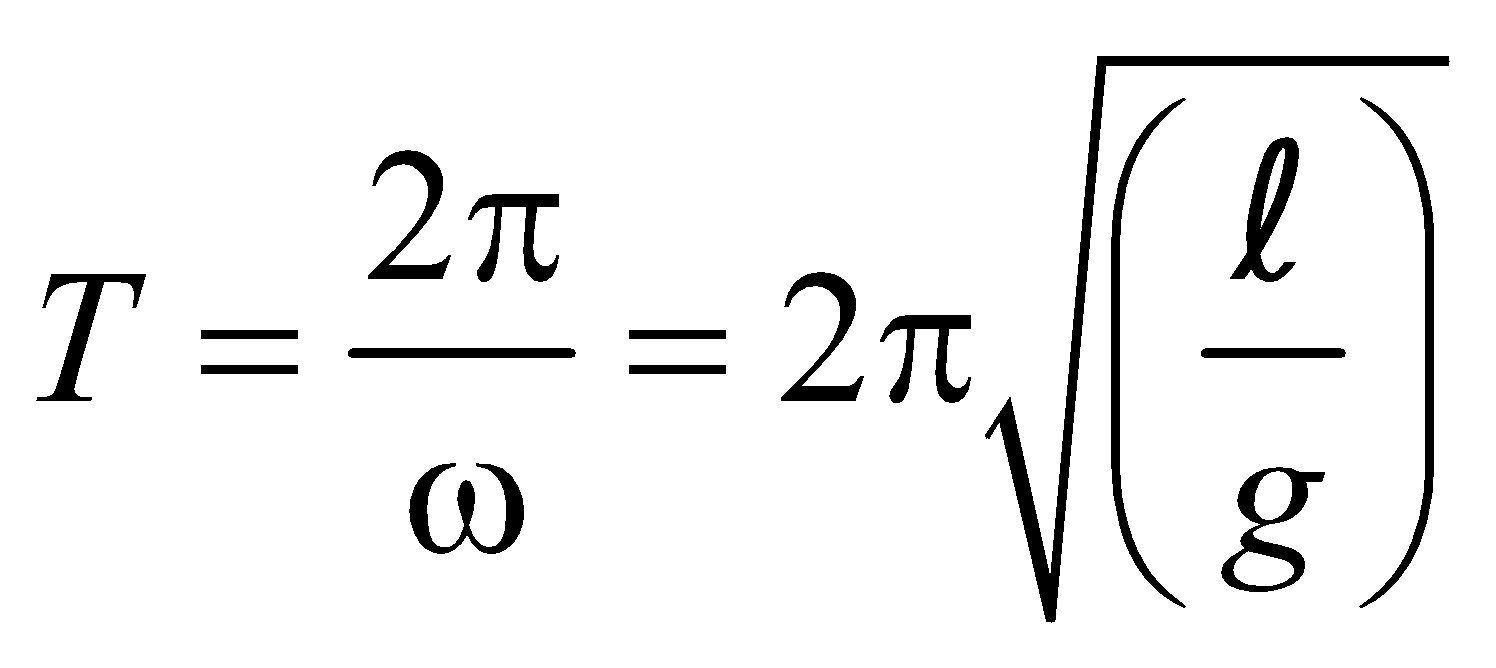
\(T_{earth}=2\pi\sqrt{\frac{l}{g_{earth}}}\)
\(T_{Merc}=2\pi\sqrt{\frac{l}{g_{Merc}}}\)
or
\(\frac{T_{Merc}}{T_{earth}}=\sqrt{\frac{g_{earth}}{g_{Merc}}}\)
\(=\sqrt{\frac{g}{0.4g}}=\sqrt{2.5}\)
\(T_{Merc}\approx 1.6T\)