Question
A group of students perform an experiment to find the refractive index of a glass block. They measure various values of the angle of incidence \(i\) and angle of refraction \(r\) for a ray entering the glass from air. They plot a graph of the \(\sin r\) against \(\sin i\).

They determine the gradient of the graph to be \(m\).
Which of the following gives the critical angle of the glass?
A. \(\sin ^{-1}(m)\)
B. \(\sin ^{-1}\left(\frac{1}{m}\right)\)
C. \(m\)
D. \(\frac{1}{m}\)
▶️Answer/Explanation
Ans:A

\(\begin{aligned} \quad & n_1 \text { sin i }=n_2 \sin r \\ & \text { Snalls Law. } \\ m(slope) = & \frac{\sin r}{\sin i}=\frac{n_1}{n_2}=\frac{1}{n}\end{aligned}\)
$n_1=1$ and $n_2 =n$
Now , TIR comes to action from which we have to calculate the critical angle (and happens only when ray goes from denser to rarer medium)

\(\begin{aligned}
& n \cdot \sin \theta_c=1 \cdot \sin 90 \\
& n \cdot \sin \theta_c=1 \Rightarrow \theta_c=\sin ^{-1}\left(\frac{1}{n}\right)\\
&\theta_c=sin ^{-1} m
\end{aligned}\)
Question
White light is incident on gas at very low pressure. The light passing through the gas is analysed. What phenomenon is being investigated?
A. Absorption spectrum
B. Emission spectrum
C. Photoelectric effect
D. Polarization
▶️Answer/Explanation
Ans:A
When white light is incident on a gas at very low pressure, and the light passing through the gas is analyzed, the phenomenon being investigated is typically the absorption spectrum. Absorption spectrum occurs when the gas absorbs certain wavelengths of light, leaving dark lines or bands in the transmitted spectrum. These lines or bands represent the specific wavelengths of light that have been absorbed by the gas, which can provide valuable information about the atomic or molecular properties of the gas. This is a common technique in spectroscopy and is used to identify the elements or molecules present in a gas.
Question
An electromagnetic wave enters a medium of lower refractive index. Three statements are made:
I. The wavelength of the wave has increased.
II. The frequency of the wave has decreased.
III. The speed of the wave has increased.
What is true about the properties of the wave?
A. I and II only
B. I and III only
C. II and III only
D. I, II and III
▶️Answer/Explanation
Ans:B
When an electromagnetic wave enters a medium with a lower refractive index, several changes occur in its properties:
I. The wavelength of the wave has increased.
This statement is correct. When an electromagnetic wave passes from a medium with a higher refractive index to a medium with a lower refractive index, the wavelength of the wave increases. This is a fundamental property of waves described by Snell’s Law.
II. The frequency of the wave has decreased.
This statement is incorrect. In the context of the same wave entering a different medium, the frequency remains constant. The frequency of an electromagnetic wave does not change when it enters a new medium; it is a fundamental property of the wave.
III. The speed of the wave has increased.
This statement is correct. When an electromagnetic wave enters a medium with a lower refractive index, its speed increases. This is a consequence of Snell’s Law, which relates the angle of incidence and the refractive indices of the two media to the speed of light in those media.
So, the correct statements are I and III. Therefore, the correct option is:
B. I and III only.
Question
Unpolarized light of intensity I and amplitude A passes through a polarizing filter.

What is the amplitude of the light transmitted by the polarizing filter?
A. \(\frac{A^2}{2}\)
B. \(\frac{A}{4}\)
C. \(\frac{A}{2}\)
D. \(\frac{A}{\sqrt{2}}\)
▶️Answer/Explanation
Ans:D
When unpolarized light passes through a polarizing filter, the intensity of the light transmitted is reduced to half of the original intensity. Intensity (\(I\)) is proportional to the square of the amplitude (\(A\)) of the wave, so we can express this relationship as:
\[I \propto A^2.\]
When we say the intensity is reduced to half, it means the new intensity (\(I’\)) is half of the original intensity (\(I\)):
\[I’ = \frac{1}{2}I.\]
Now, we need to find the new amplitude (\(A’\)) after the light has passed through the polarizing filter. We know that intensity is proportional to the square of the amplitude, so we can write:
\[I’ \propto (A’)^2.\]
Since \(I’ = \frac{1}{2}I\), we have:
\[\frac{1}{2}I \propto (A’)^2.\]
Now, let’s solve for \(A’\):
\[(A’)^2 = \frac{1}{2}I.\]
To find \(A’\), take the square root of both sides:
\[A’ = \sqrt{\frac{1}{2}I}.\]
Now, let’s use the fact that intensity (\(I\)) is proportional to the square of amplitude (\(A\)):
\[I \propto A^2 \implies I = kA^2,\]
where \(k\) is a constant of proportionality. Now, we can rewrite the expression for \(A’\) as:
\[A’ = \sqrt{\frac{1}{2}\cdot kA^2}.\]
Since the proportionality constant remains the same, we have:
\[A’ = \sqrt{\frac{k}{2}}A.\]
Now, we can see that \(A’\) is proportional to \(A\) with the constant of proportionality \(\sqrt{k/2}\).
So, the amplitude of the light transmitted by the polarizing filter is reduced to \(\sqrt{k/2}\) times the original amplitude (\(A\)).
D. \(\frac{A}{\sqrt{2}}\).
Question
Wavefronts travel from air to medium Q as shown.
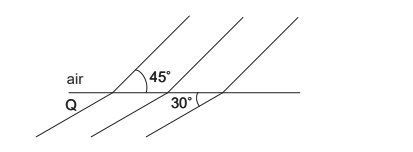
What is the refractive index of Q?
A
B
C
D
Answer/Explanation
Ans: B
Refe: https://www.iitianacademy.com/ib-dp-physics-topic-4-waves-4-4-wave-behavior-study-notes/
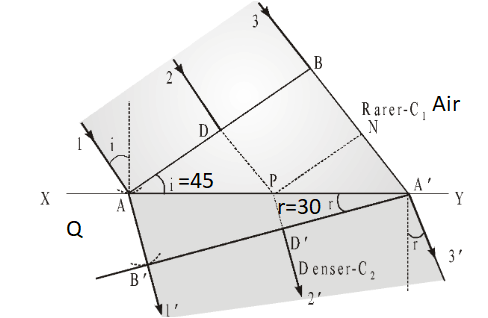
\(\frac{n_1}{n_2}=\frac{sin \theta_2}{sin \theta_1} \; snell \;law\)
\(\frac{n_{air}}{n_Q}=\frac{sin\; r}{sin\;i}\)
\(\therefore n_Q =n_{air}\times\frac{sin\;i}{sin\; r} =\frac{sin \;45^0}{sin \;30^0}\)
\(\because n_{air} =1\)
\(\therefore n_Q =\frac{sin \;45^0}{sin \;30^0}\)\)