Question
A standing wave is formed in a pipe open at one end and closed at the other. The length of the pipe is L and the speed of sound in the pipe is V.

\(n\) is a positive integer.
What expression is correct about the frequencies of the harmonics in the pipe?
A. \(\frac{(2 n-1) V}{2 L}\)
B. \(\frac{(2 n-1) V}{4 L}\)
C. \(\frac{n V}{2 L}\)
D. \(\frac{n V}{4 L}\)
▶️Answer/Explanation
Ans:B
The general frequency for closed at one end and open to other is ,
\(f_n=\frac{n \cdot w}{4 L} \quad n\)-odd Number and even Harmonics are not present in this.
But in question $n$ is given positive number which it has even as well as odd to , so we have to exclude the even one , and for that we will replace n to $2n+1/2n-1$
\(f_n=\frac{2n+1 \cdot w}{4 L}\) or \(f_n=\frac{2n-1 \cdot w}{4 L}\)
Correct match option – B
Question
A pipe containing air is closed at one end and open at the other. The third harmonic standing wave for this pipe has a frequency of \(150 \mathrm{~Hz}\).
What other frequency is possible for a standing wave in this pipe?
A. \(25 \mathrm{~Hz}\)
B. \(50 \mathrm{~Hz}\)
C. \(75 \mathrm{~Hz}\)
D. \(300 \mathrm{~Hz}\)
▶️Answer/Explanation
Ans:B
In a closed-open pipe (like an open-end organ pipe), the fundamental frequency (first harmonic) is produced when the length of the pipe is one-fourth (1/4) of the wavelength of the sound wave. In this case, the pipe is closed at one end and open at the other.
The third harmonic has a frequency of \(150 \, \text{Hz}\), which means that the pipe length corresponds to one and a half wavelengths (\(\lambda/2\)). The fundamental frequency (\(f_1\)) corresponds to a quarter-wavelength (\(\lambda/4\)).
So, if the third harmonic is at \(150 \, \text{Hz}\), we can find the fundamental frequency (\(f_1\)) as follows:
\(\frac{f_3}{f_1} = \frac{\lambda_3}{\lambda_1} = \frac{3}{1}\)
\(f_1 = \frac{f_3}{3} = \frac{150 \, \text{Hz}}{3} = 50 \, \text{Hz}\)
Therefore, the possible frequency for a standing wave in this pipe, other than the third harmonic, is the fundamental frequency, which is \(50 \, \text{Hz\).
Question
The diagram shows a second harmonic standing wave on a string fixed at both ends.
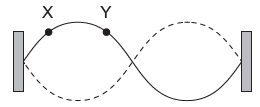
What is the phase difference, in rad, between the particle at X and the particle at Y?
A. 0
B. \(\frac{\pi }{4}\)
C. \(\frac{\pi }{2}\)
D. \(\frac{{3\pi }}{4}\)
Answer/Explanation
Markscheme
A
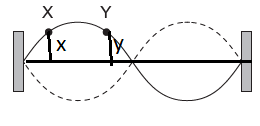
We have phase difference \(\phi \) as
\(\phi = \frac{2\pi}{\lambda}\times \Delta x\)
here
\(\Delta x =x-y=0\)
hence
\(\phi =0\)
Question
The air in a pipe, open at both ends, vibrates in the second harmonic mode.
![]()
P Q
![]()
What is the phase difference between the motion of a particle at P and the motion of a particle at Q?
A 0
B
C π
D 2π
Answer/Explanation
Answer – C
For an open organ pipe, the length L is given as
\(L=n\frac{\Lambda }{2}\)
where, λ is the wavelength of wave and n is an integer and by putting n = 1,2,3,…………… we get the modes of vibration.
n=1 gives first harmonics, n=2 gives second harmonics and so on.
Here, an open organ pipe of length L vibrates in second harmonic mode,
hence the length of pipe is
\(L=\frac{2\Lambda }{2}=\Lambda\)
\(L=\Lambda\)
And P and Q at \(\frac{\Lambda }{2}\)
Phase difference \(=\frac{2\pi }{\Lambda }\left ( \Delta x \right )\) path difference.
Which is equal to \(\pi \)
Water is draining from a vertical tube that was initially full. A vibrating tuning fork is held near the top of the tube. For two positions of the water surface only, the sound is at its maximum loudness.

The distance between the two positions of maximum loudness is x.
What is the wavelength of the sound emitted by the tuning fork?
A. \(\frac{x}{2}\)
B. x
C. \(\frac{{3x}}{2}\)
D. 2x
Answer/Explanation
Markscheme
D