Question
Three identical secondary coils, \(\mathrm{P}, \mathrm{Q}\) and \(\mathrm{R}\), are wound onto the iron core of a transformer. The coils form a power supply that provides two output voltages, one between \(A\) and \(B\) and another between \(\mathrm{C}\) and \(\mathrm{D}\).
The primary coil of the transformer is connected to a \(110 \mathrm{~V} r m s\) mains supply.
The primary coil has 1500 turns. Each secondary coil has 75 turns.

(a) Two of the secondary coils, P and Q, are connected in series to a diode bridge. There is no load resistor between A and \(B\).
\(\mathrm{X}\) and \(\mathrm{Y}\) are points in the circuit connected to the ends of the coils.
(i) Calculate the peak emf between \(\mathrm{X}\) and \(\mathrm{Y}\). [2]
(ii) The graph shows the variation with time of the output emf between X and Y.

Draw, on the graph, the variation with time of the potential difference between \(A\) and \(B\). You do not need to put numbers on the axes.[1]
(b) A resistor is now connected between \(A\) and \(B\).
State and explain the reason why the peak potential difference across \(X Y\) will be smaller than the emf you calculated in (a)(i).[2]
(c) Coil R is connected to a single diode and a load that consists of a capacitor and a resistor.
The graph shows the variation with time of the potential difference across coil \(\mathrm{R}\).

Sketch, on the graph, the potential difference between C and D.
(d) State and explain the effect of adding another capacitor in parallel with the original capacitor.[2]
▶️Answer/Explanation
Ans:
a i Use of \(\sqrt{2} \times \frac{n_8}{n_p}\) OR correct conversion of ms to peak value at some point \(16 \propto V w\)
ii Output emf

b.There is now a current in the secondary coils
Energy loss due to heating in the coils
OR
\&Lenz’s law predicts that this will oppose the original induced emf sand reduce the pd across the coils”

d.Adding a capacitor in parallel will increase the capacitance / will increase RC \(\checkmark\) idea that this makes the waveform smoother \(\checkmark\)
Question
A vertical rectangular loop of conducting wire is dropped in a region of horizontal magnetic field. The diagram shows the loop as it leaves the region of the magnetic field.
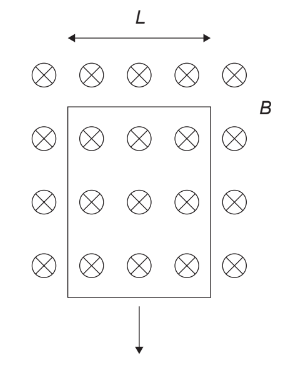
(a) Explain, by reference to Faraday’s law of electromagnetic induction, why there is an electromotive force \((\mathrm{emf})\) induced in the loop as it leaves the region of magnetic field. [2]
(b) Just before the loop is about to completely exit the region of magnetic field, the loop moves with constant terminal speed \(v\).
The following data is available:

Determine, in \(\mathrm{ms}^{-1}\) the terminal speed \(v\).
(c) Three capacitors \(C_1=3.0 \mu \mathrm{F}, C_2=2.0 \mu \mathrm{F}\) and \(C_3=4.0 \mu \mathrm{F}\) are connected to a cell of emf \(12 \mathrm{~V}\) and negligible internal resistance. The capacitors are initially uncharged.

Calculate
(i) the total capacitance of the circuit.[2]
(ii) the total energy stored in the three capacitors.[1]
(iii) the charge on \(\mathrm{C}_2\).[3]
▶️Answer/Explanation
Ans:
The induced emf is equal/proportional/related to the «rate of» change of «magnetic» flux/flux linkage
Flux is changing because the area pierced/enclosed by magnetic field lines changes «decreases»
OR
Flux is changing because the loop is leaving/moving out of the «magneticn field.
b.\(\begin{aligned} & m g=B I L O R I=0.33 \propto A » \checkmark \\ & B v L=I R \text { OR } \mathcal{E}=8.25 \times 10^{-3} \alpha V_n \text { OR } \varepsilon=0.12 v \checkmark \\ & \text { Combining results to get } v=\frac{m g R}{B^2 L^2} \checkmark \\ & v=\alpha \frac{0.0040 \times 9.81 \times 0.025}{0.80^2 \times 0.15^2}=n 0.068 \kappa^2 \mathrm{~ms}^{-1} n \\ & \end{aligned}\)
c i The 2 in parallel give a total of \(6.0\left\langle\mu \mathrm{F}_\eta \checkmark\right.\) The total is \(4\left(\frac{1}{3}+\frac{1}{6}\right)^{-1} »=2.0\langle\mu \mathrm{F} » \checkmark\)
ii \(E=\ll \frac{1}{2} C V^2=\frac{1}{2} \times 2.0 \times 10^{-6} \times 12^2 » 1.44 \times 10^{-4} \ll J_{\Downarrow}\)
iii ALTERNATE 1
Voltage across \(\mathrm{C}_2\) is half that across \(\mathrm{C}_1 \checkmark\)
So voltage across \(\mathrm{C}_2\) is \(4.0 \mathrm{~V} \checkmark\)
Charge is \(« C_2 V_2=2.0 \times 10^{-6} \times 4.0 m 8.0 \times 10^{-6} \ll C » v\)
ALTERNATE 2
Charge on \(C_1\) is \(\alpha C_T V_T=2.0 \times 10^{-6} \times 12 m 24 \ll \mu C_n \checkmark\)
So voltage across \(C_1\) is \(₫ \frac{24}{3.0} m 8.0 \ll \mathrm{V} m v\)
Charge on \(C_2\) is \(« C_2 V_2=2.0 \times 10^{-6} \times 4.0 » 8.0 \times 10^{-6} \ll \mathrm{C} » \checkmark\)
ALTERNATE 3
\(\alpha \mathrm{C}_3=2 \mathrm{C}_2\) leading to \(” \mathrm{q}_3=2 \mathrm{q}_2 \checkmark\)
Total charge in parallel \(=\propto q_2+q_3=q_2+2 q_2=\gg 3 q_2 \checkmark\)
\(3 \mathrm{q}_2=24\) leading to \(\mathrm{q}_2=8 \times 10^{-6} \mathrm{\alpha C}\)