- IB DP Physics SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
Learning Objectives
- State Kepler’s three laws of motion
- Solve problems using Newton’s Law of Gravitation between two spherical masses, where the masses are assumed to have uniform density and mass is concentrated at the centre
- Recognise that when astronomical objects are in orbit, the gravitational force is equal to the centripetal force
- Recall the definition for gravitational field strength
- Determine the resultant gravitational field strength due to two bodies (restricted to points along the straight line adjoining the bodies)
- Sketch the gravitational field lines for:
i) radial field surrounding point or spherical masses and
ii)uniform field close to the surface of massive celestial bodies and planetary bodies
- Define gravitational potential energy and determine the potential energy of a point mass
- Recognise gravitational potential, Vₚ, as a scalar and defined as the work per unit mass in bringing a small test mass from infinity to point P
- Recognise the magnitude of the gravitational field as the rate of change of potential with distance
- Draw equipotential lines on gravitational fields and explain that moving between equipotential lines requires work to be done on the point mass
- Define escape speed and solve problems involving the speed required for an object to escape the gravitational field of a planet
- Describe the qualitative effect of a small viscous drag force due to the atmosphere on the height and speed of an orbiting body.
Essential Idea:
The Newtonian idea of gravitational force acting between two spherical bodies and the laws of mechanics create a model that can be used to calculate the
motion of planets.
Understandings:
- Newton’s law of gravitation
- Gravitational field strength
Applications and Skills:
- Describing the relationship between gravitational force and centripetal force
- Applying Newton’s law of gravitation to the motion of an object in circular orbit around a point mass
- Solving problems involving gravitational force, gravitational field strength, orbital speed and orbital period
- Determining the resultant gravitational field strength due to two bodies
Data booklet reference:
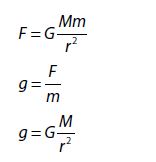
Newton’s law of gravitation:
Equation: Gravitational force = \(F_g=\frac{GM_1M_2}{r^2}\), where M1 and M2 are two different objects’ masses, r is the distance between them and G the universal gravitational constant, which is equal to 6.67 x 10^-11 Nm^2kg^-2
Direction: Gravitational force is always attractive and acts on every body with mass.
Point mass: For a spherical body with uniform density, the entire mass may be assumed to be concentrated at its center, and so the body may be assumed to be a point mass.
Gravitational field strength (g)
Definition: “Gravitational field strength is the gravitational force per unit mass experienced by a small point mass placed at a certain point”.
It is a vector.
Equation: \(g=\frac{F}{m}=\frac{GM}{r^2}\), where M is the Mass influencing the small point mass.
Units: \(ms^{-2}\)
At Earth \(g=9.8 \; ms^{-2}\)
Field lines: Towards body’s center of mass.
Tip: Why passengers feel as if they are being thrown outwards when in turning on a horizontal road?
“Passengers are in a rotating frame of reference Seen from above the passengers would move in a straight line, according do Newton’s First Law of Motion, but friction acts at the seat to provide centripental force to centre of circle. Passengers interpret the reaction to this force as being flung outwards”.
GRAVITATION
NEWTON’S UNIVERSAL LAW OF GRAVITATION
- The gravitational force is the central force and follows inverse square law. It acts along the line joining the particles.
- Since the work done by the gravitational force is independent of the path followed and hence it is a conservative force.
- It is the weakest force in nature. It is 1038 times smaller than nuclear force and 1036 times smaller than electric force. Strongest force being nuclear force (for small range) followed by electric force.
- Gravitation is independent of the presence of other bodies around it.
ACCELERATION DUE TO GRAVITY (g)
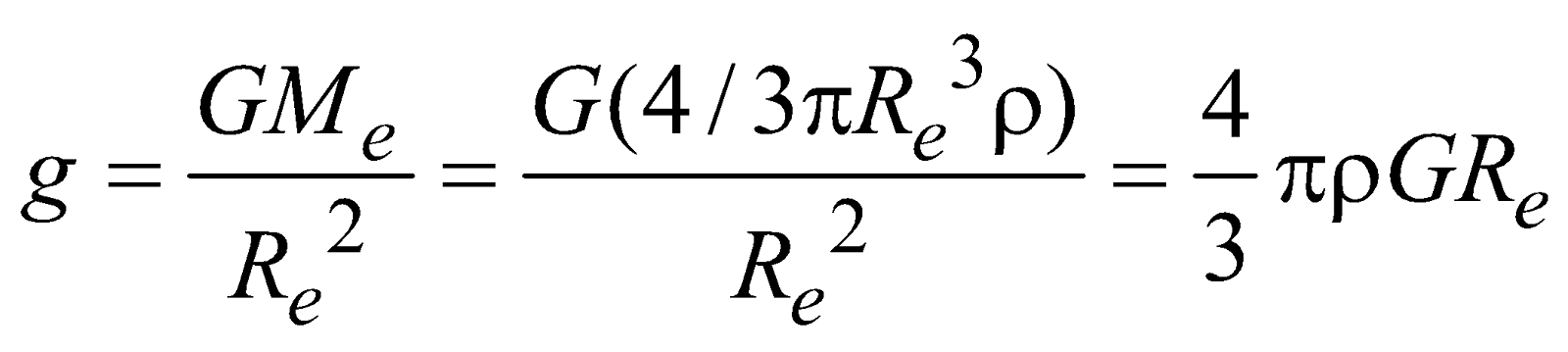 ……(iv)
……(iv)CHANGE IN THE VALUE OF ACCELERATION DUE TO GRAVITY (g)
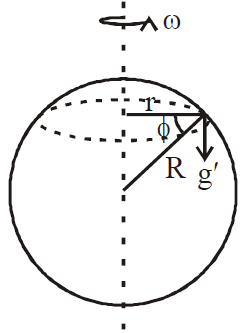
- Due to rotation or latitude of earth
- Due to shape of earth
- At a depth ‘d’ below the earth surface
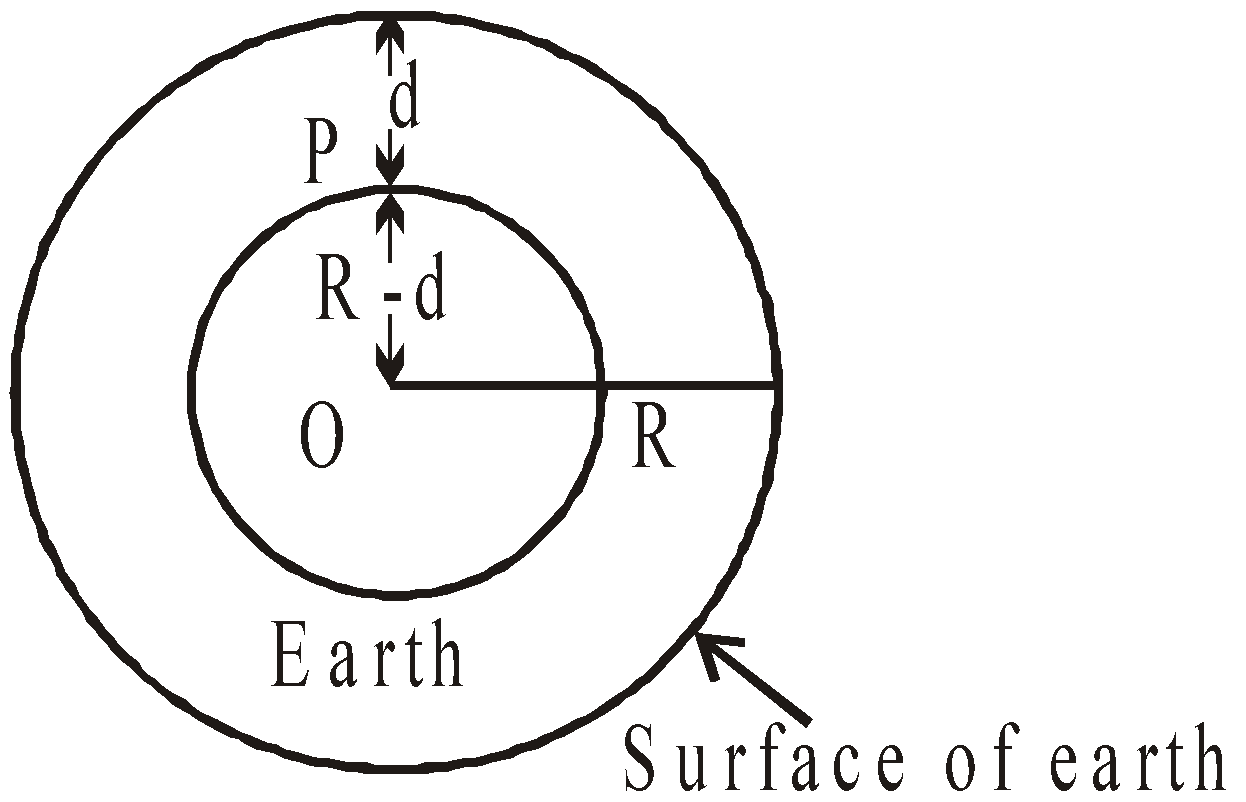
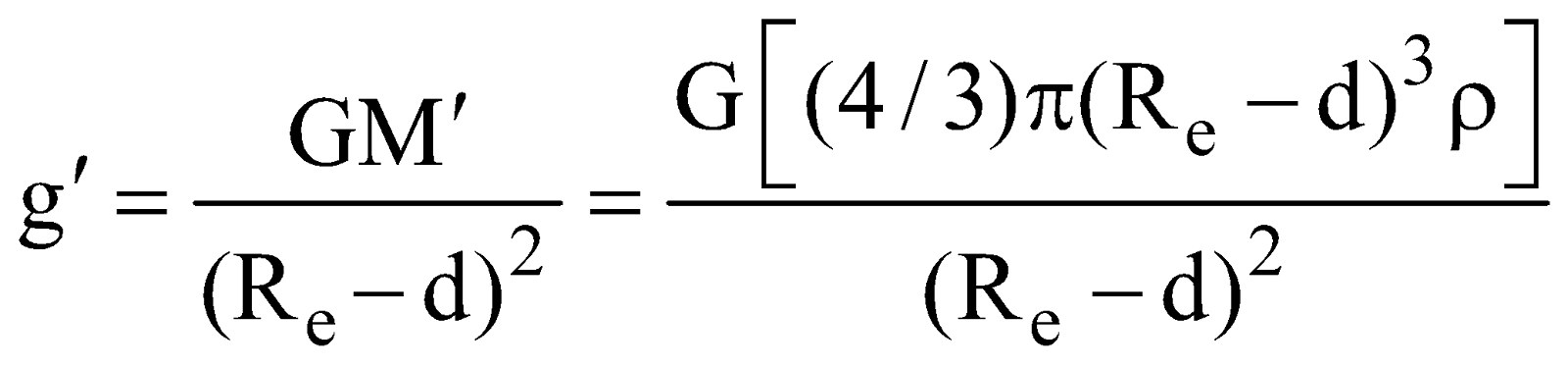
- At a height ‘h’ above the earth surface
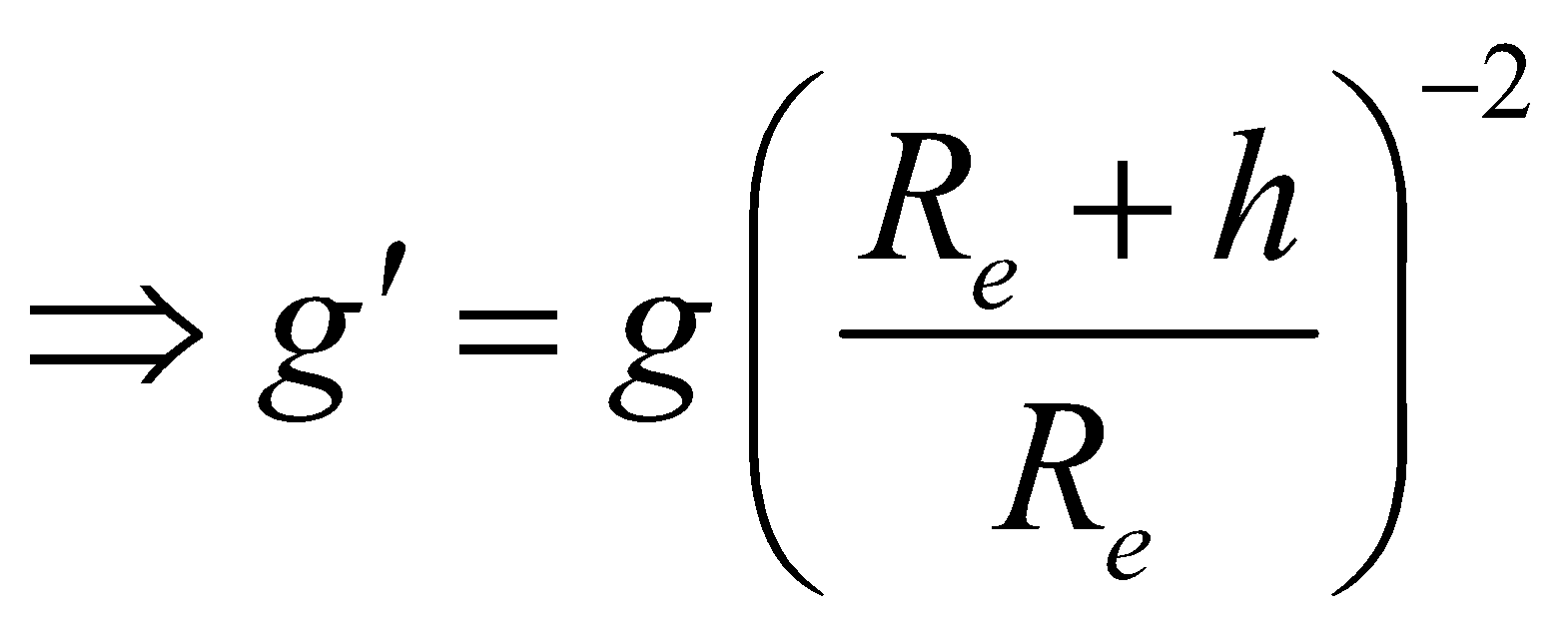 [from eqs. (ix) & (x)]
[from eqs. (ix) & (x)]
- The value of the acceleration due to gravity on the moon is about one sixth of that on the earth and on the sun is about 27 times that on the earth.
- The value of g is minimum on the mercury, among all planets.
- For h<<R, the rate of decrease of the acceleration due to gravity with height is twice as compared to that with depth.
- The value of g increases with the increase in latitude. Its value at latitude θ is given by : gθ= g – Rω2 cos2θ.
- Rotation of the earth about its own axis is responsible for decrease in the value of g with latitude.
- The weight of the body varies along with the value of g (i.e. W = mg)
- Inertial mass and gravitational mass –
- Inertial mass (Mi) defined by Newton’s law of motion
- Gravitational mass Mg defined by Newton’s law of gravitation
- If two spheres of same material, mass and radius are put in contact, the gravitational attraction between them is directly proportional to the fourth power of the radius.
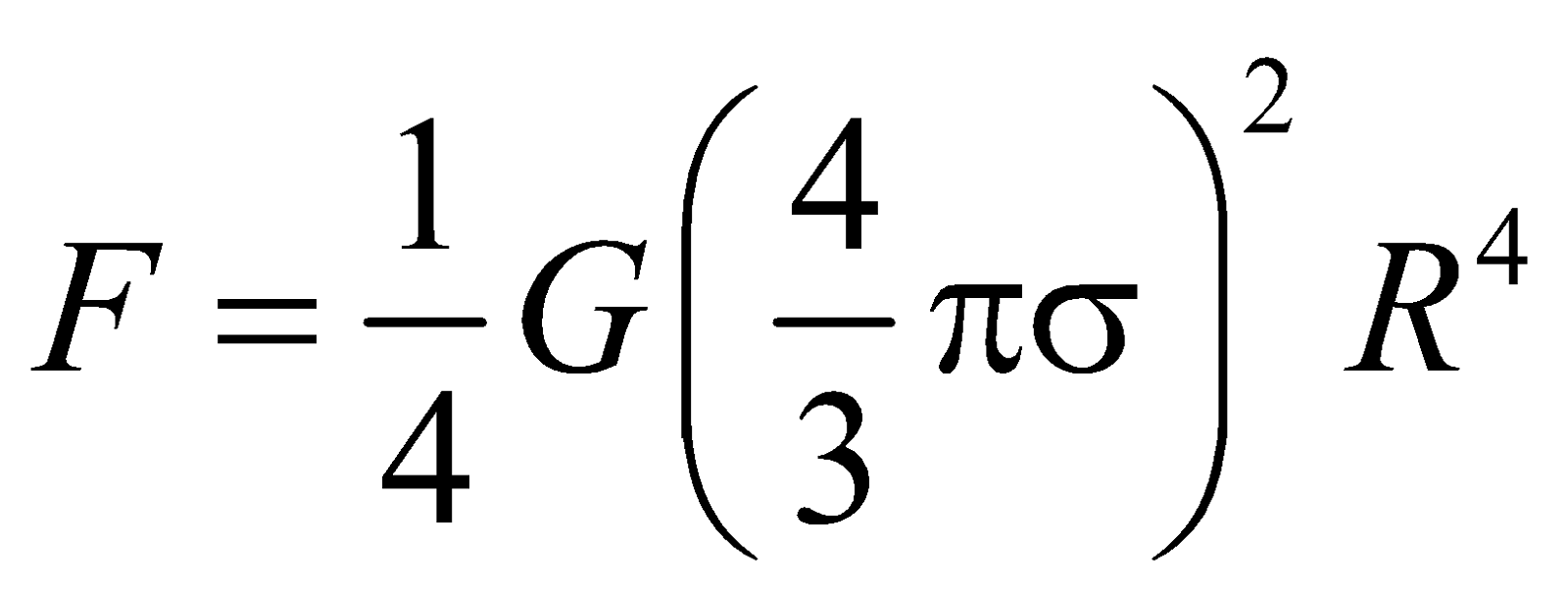
- If the earth stops rotating about its axis, the value of g at the equator will increase by about 0.35%, but that at the poles will remain unchanged.
- If the radius of planet decreases by n%, keeping the mass unchanged, the acceleration due to gravity on its surface increases by 2n%. i.e.,
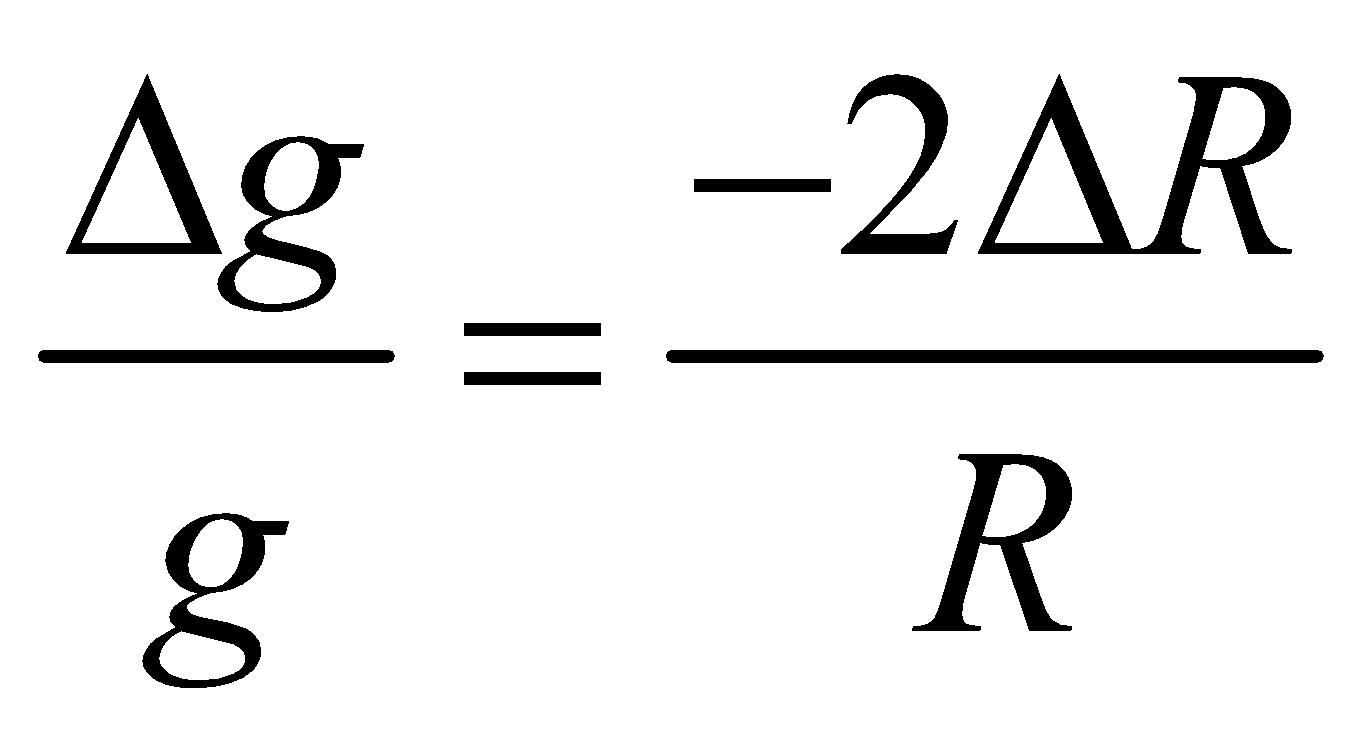
- If the mass of the planet increases by m% keeping the radius constant, the acceleration due to gravity on its surface increases by m% i.e.,
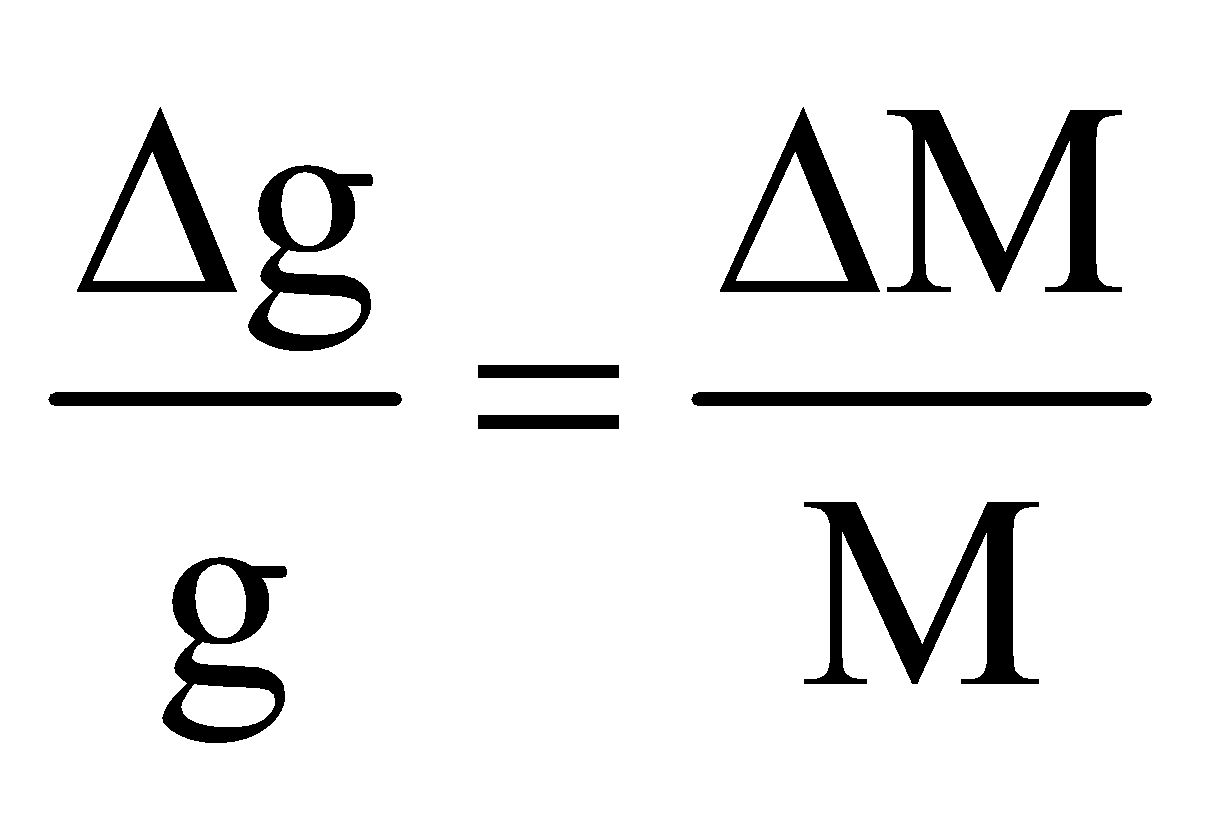 where R = constant.
where R = constant. - If the density of planet decreases by ρ% keeping the radius constant, the acceleration due to gravity decreases by ρ%.
- If the radius of the planet decreases by r% keeping the density constant, the acceleration due to gravity decreases by r%.
GRAVITATIONAL FIELD
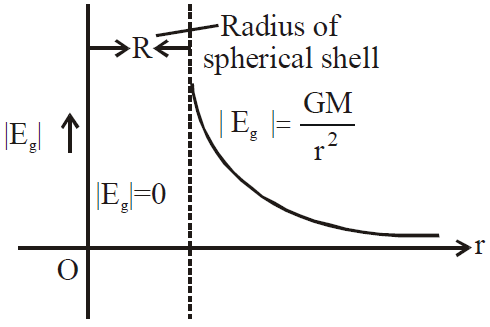
- |Eg|= 0 at points inside the spherical shell (i.e. r < R)
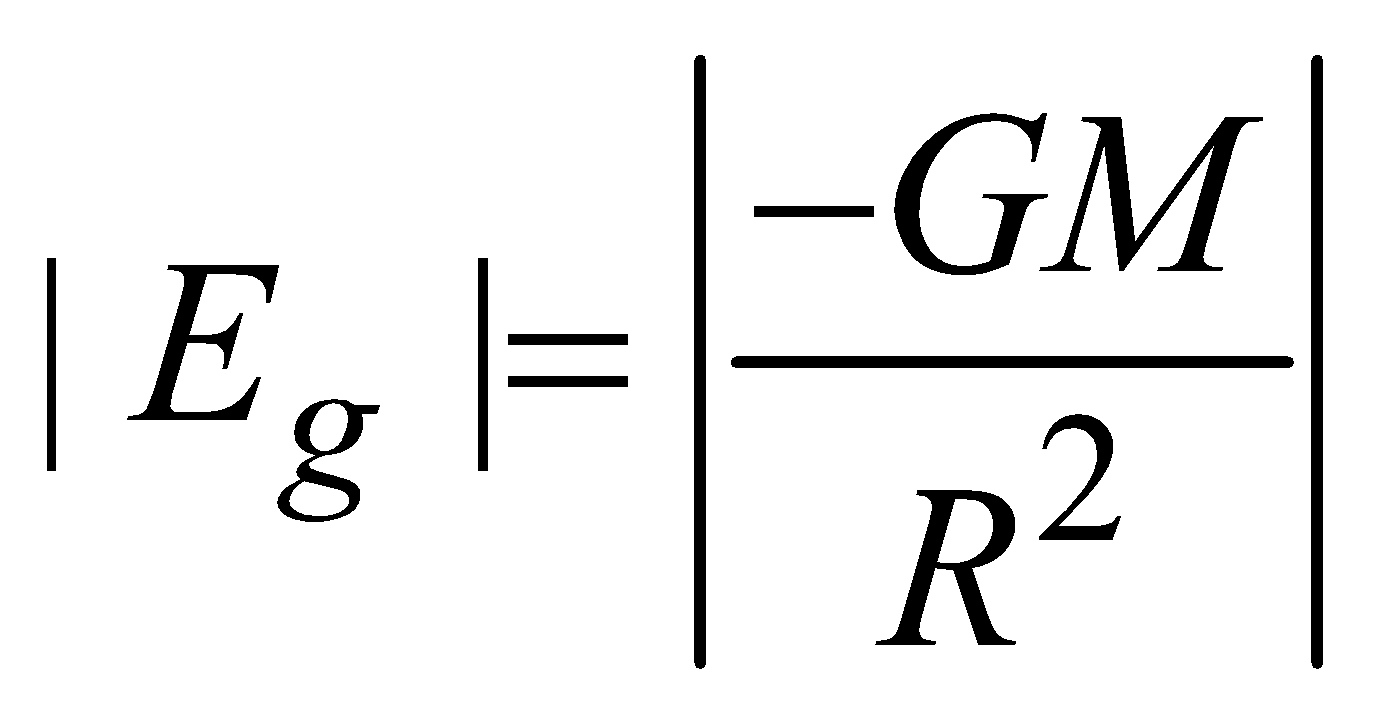 at the surface of shell (i.e. r = R)
at the surface of shell (i.e. r = R)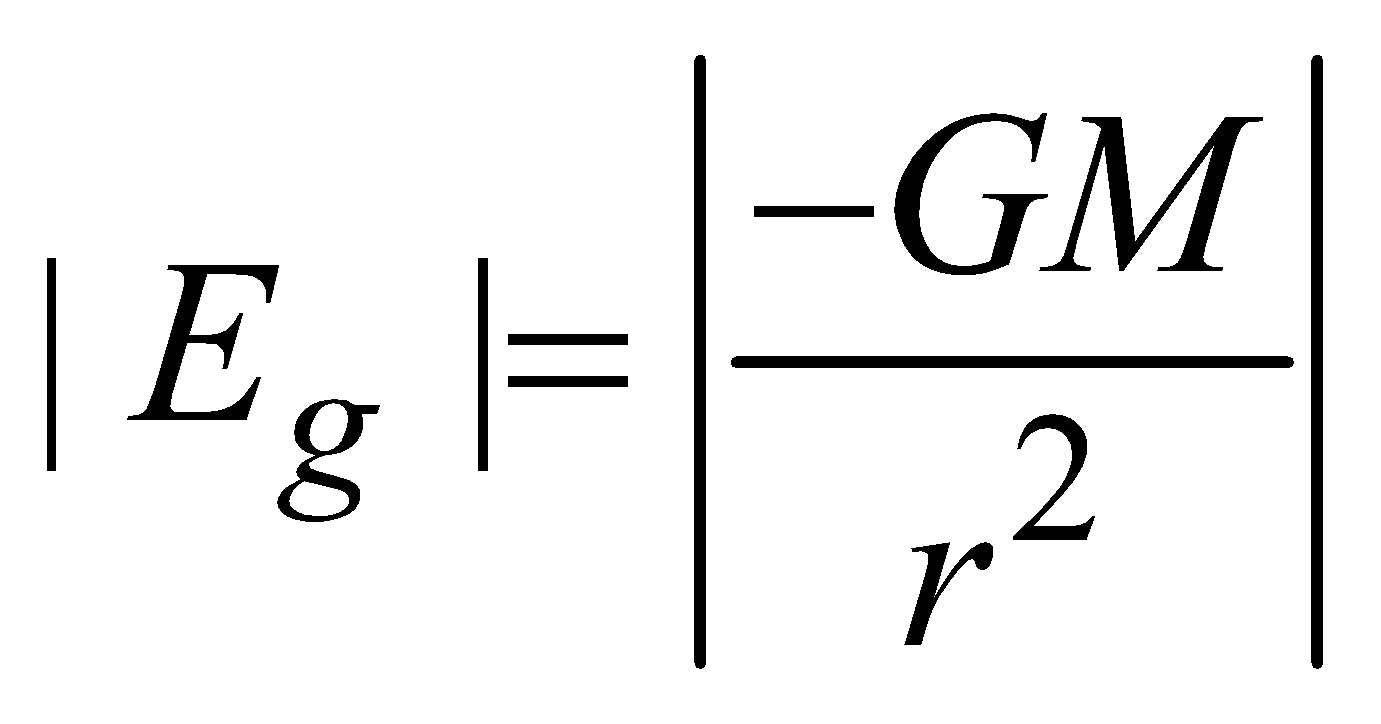 for outside the spherical shell (r >R)
for outside the spherical shell (r >R)
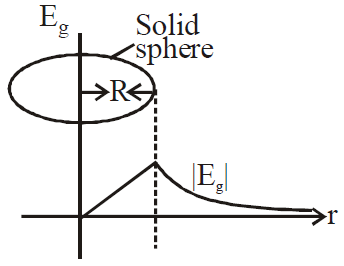
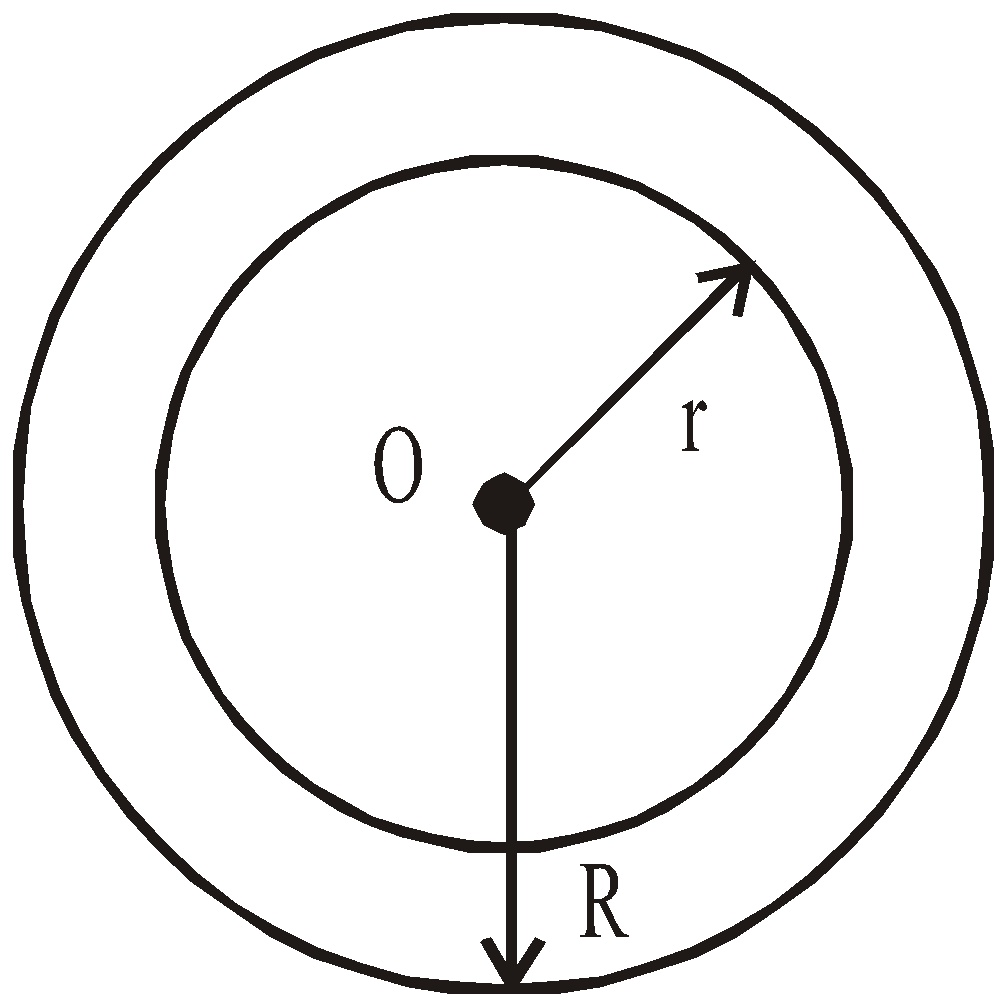
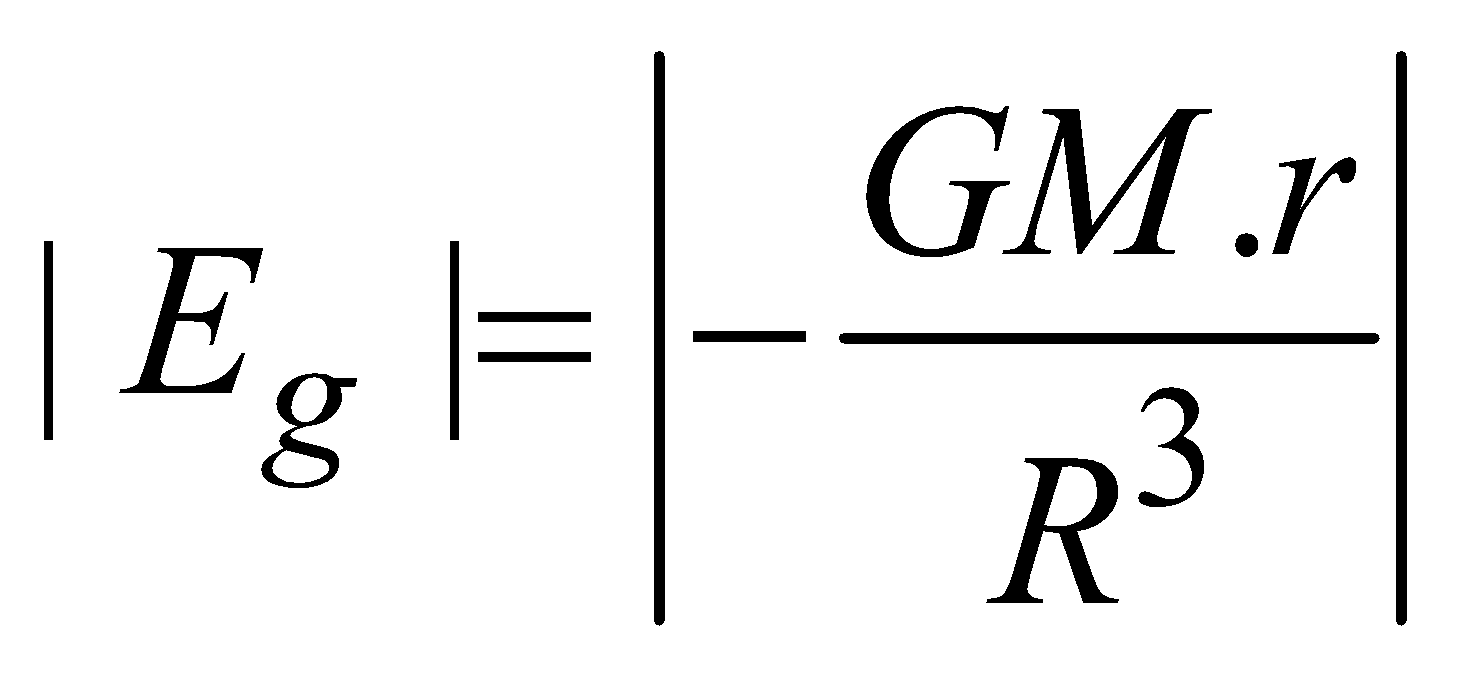 for points inside the solid sphere (r<R)
for points inside the solid sphere (r<R) 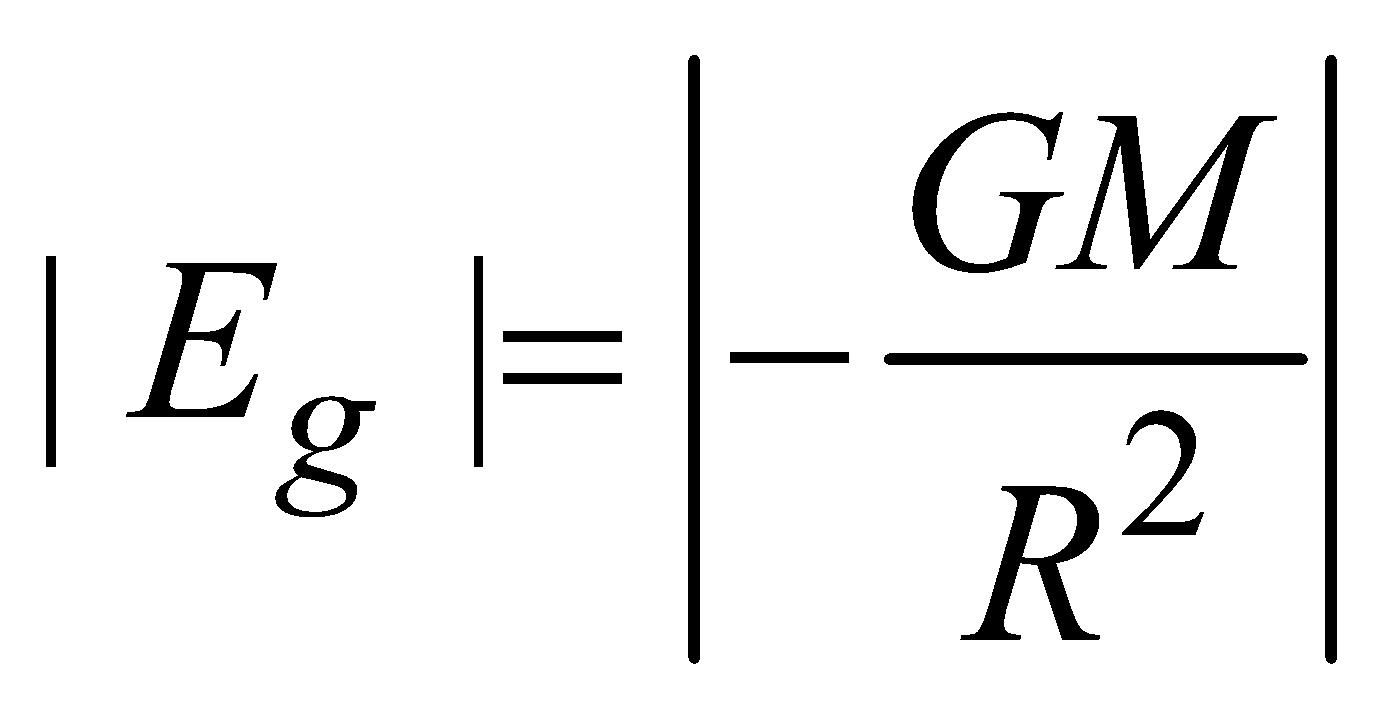 At the surface of solid sphere (r = R)
At the surface of solid sphere (r = R) 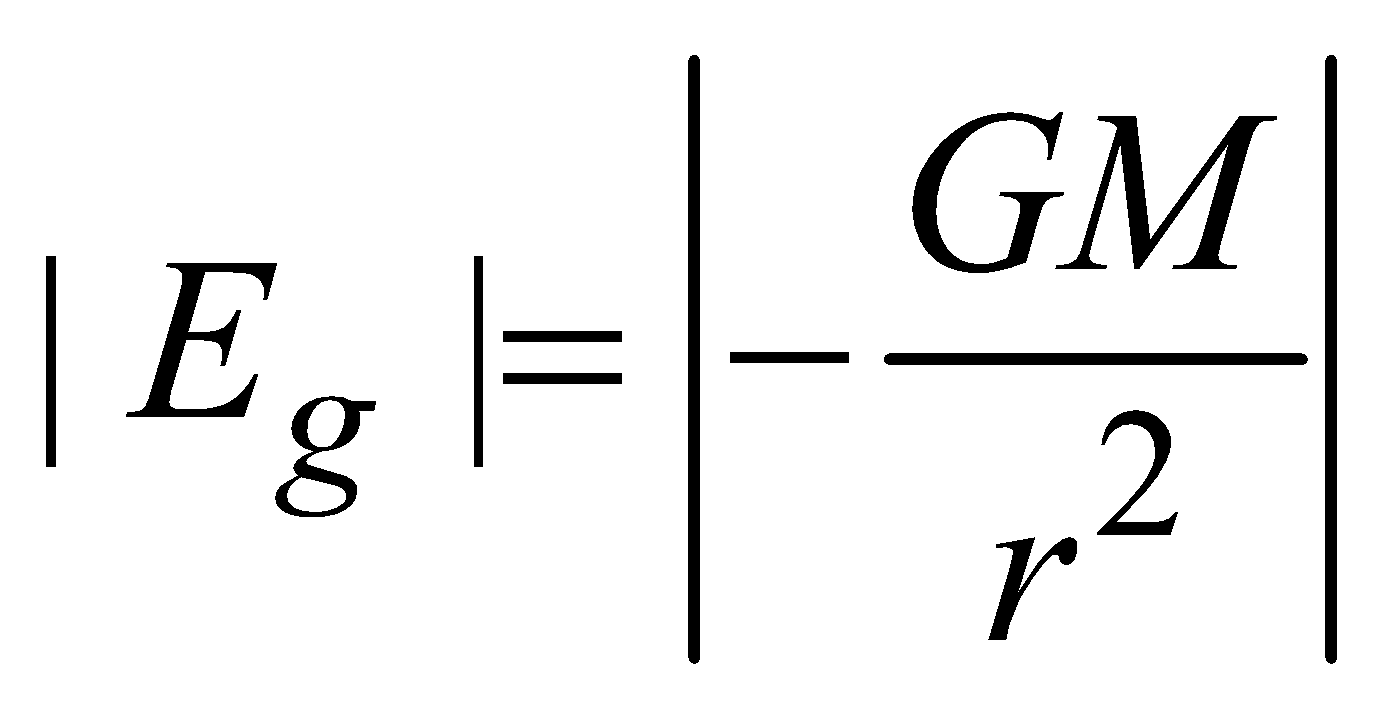 Outside the solid sphere (r > R)
Outside the solid sphere (r > R)
GRAVITATIONAL POTENTIAL
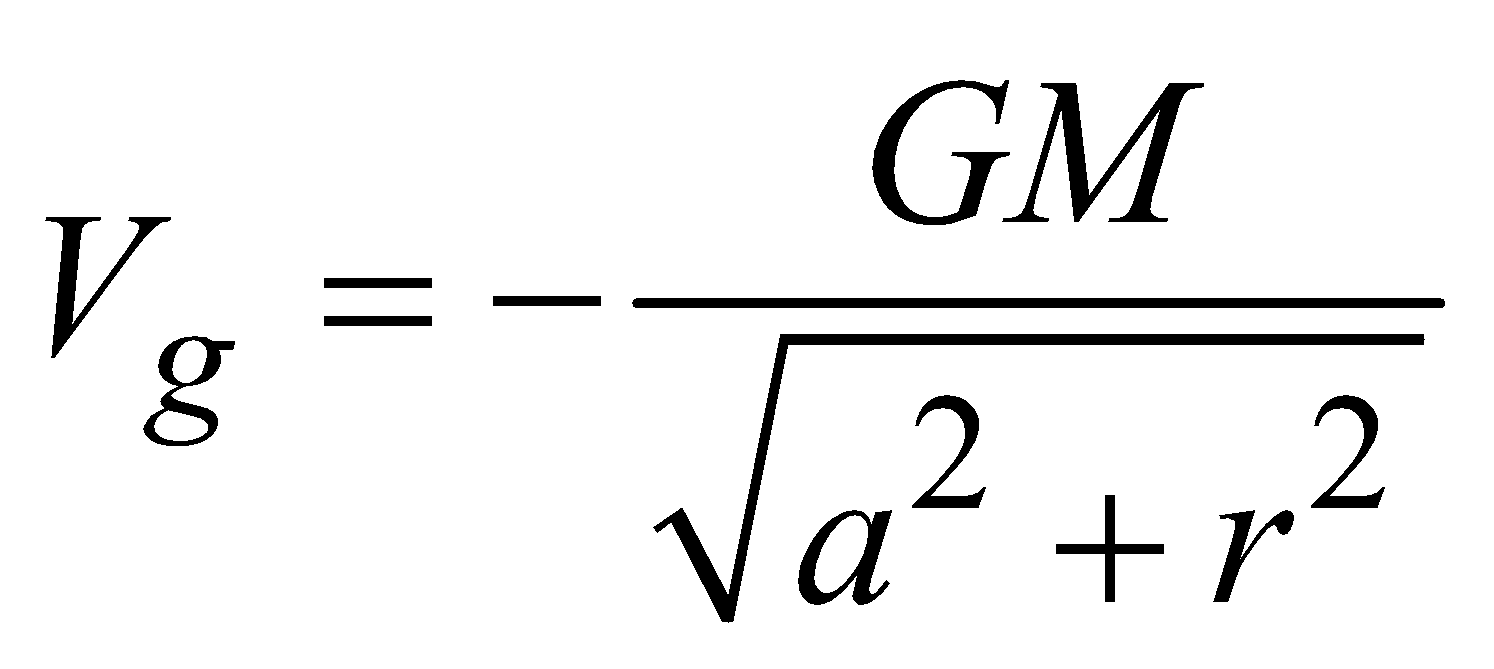
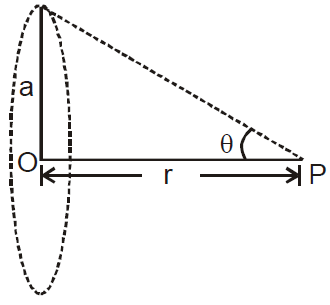
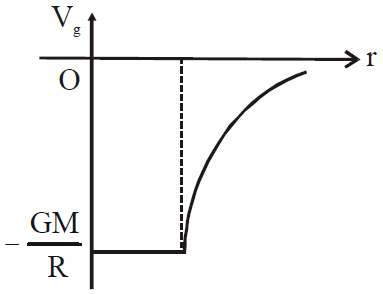
- at a point outside the shell,
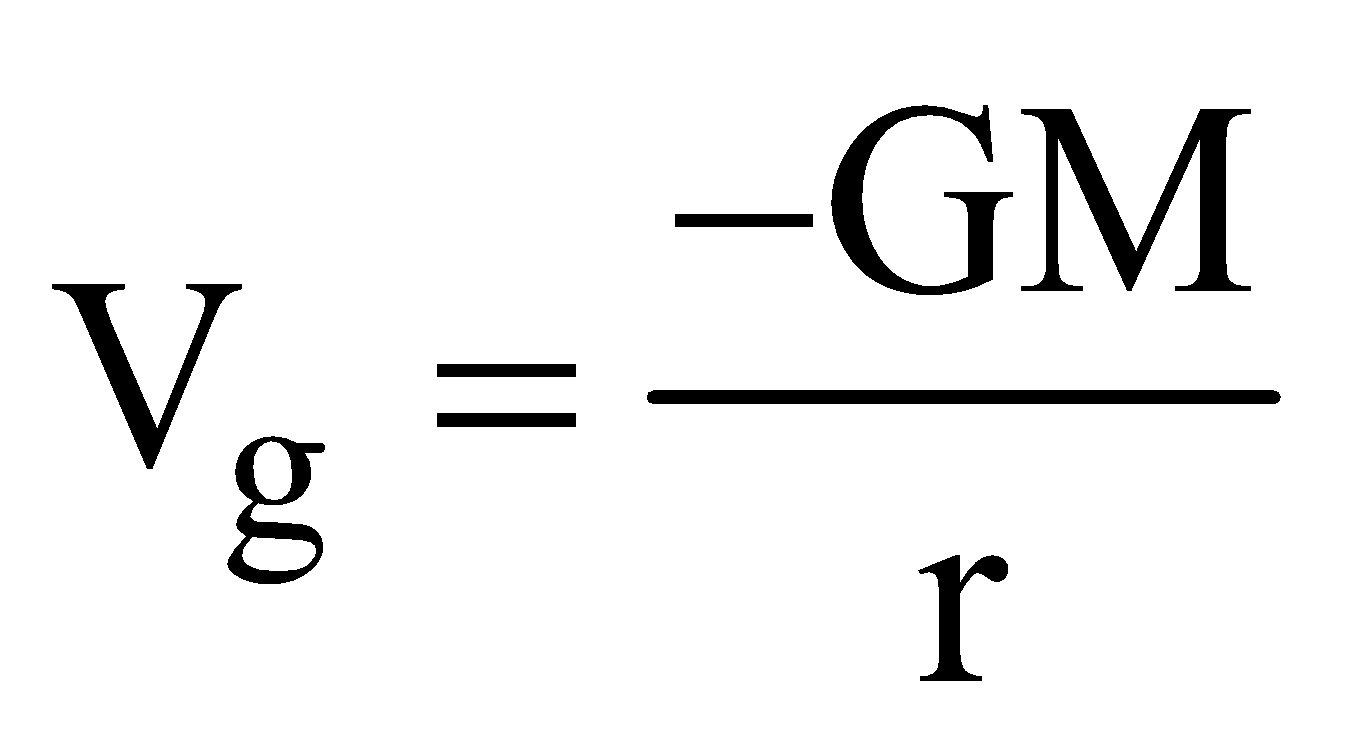 (r > R)
(r > R) - at a point inside the shell,
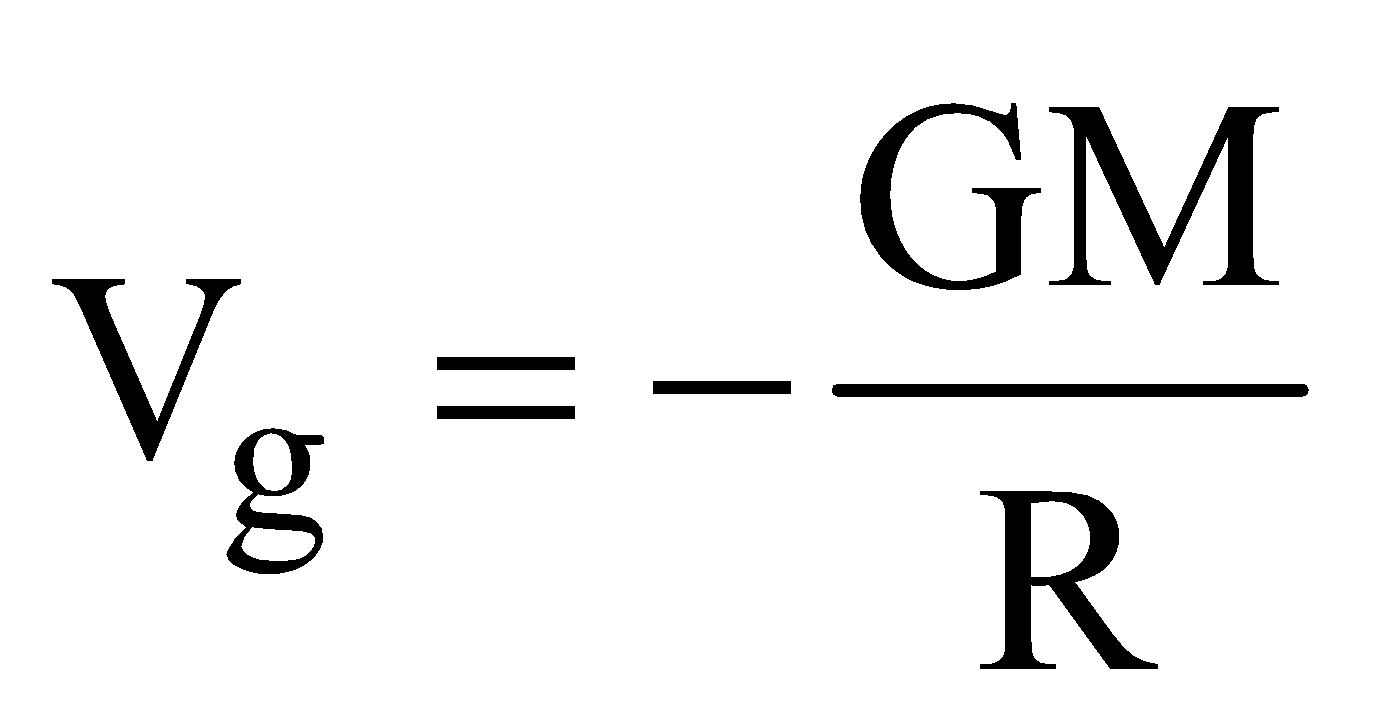 (r < R)
(r < R)
- at an external point
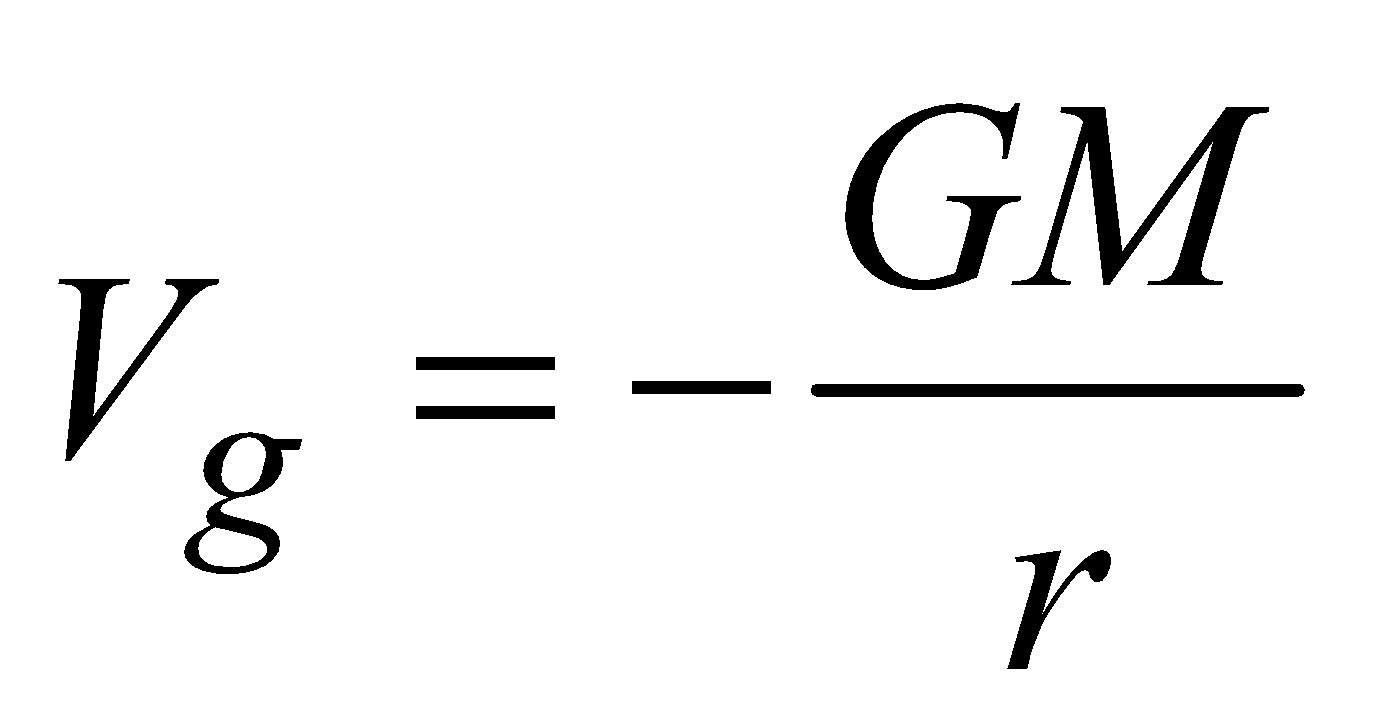 (r≥ R)
(r≥ R)
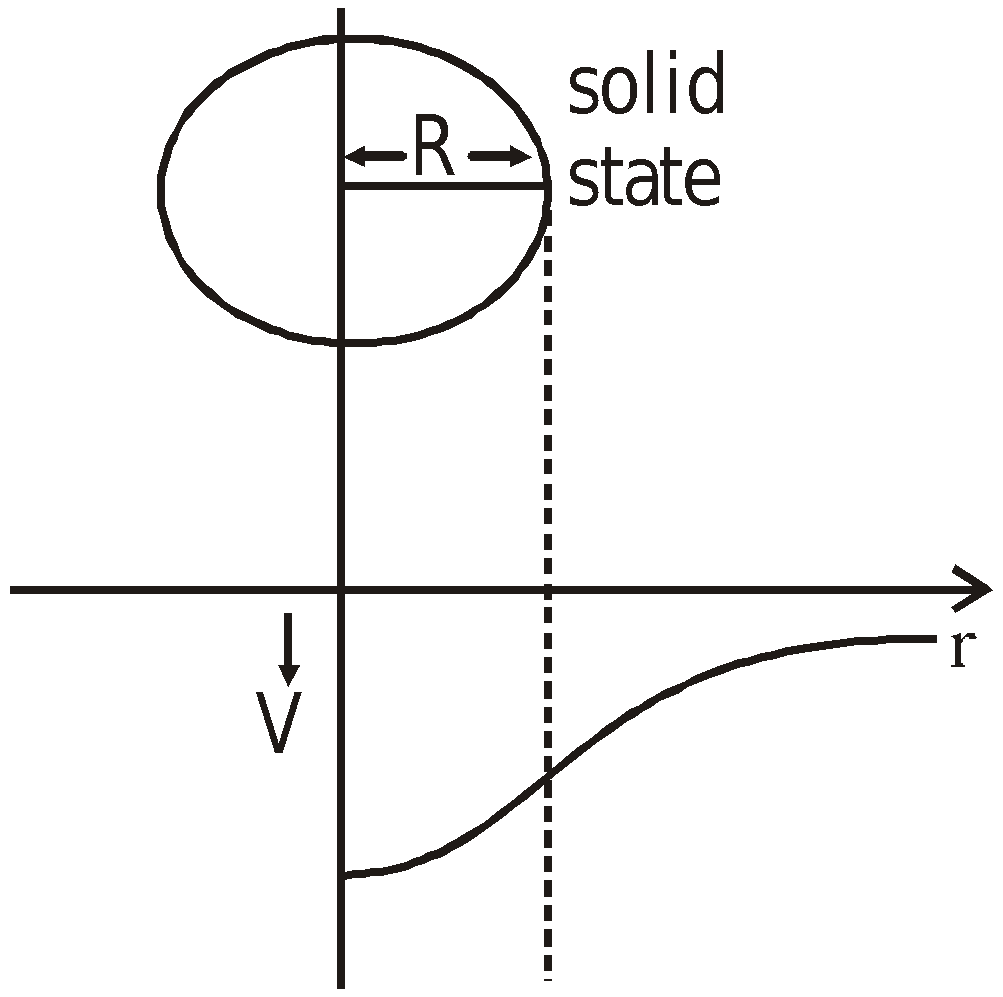
- at an internal point
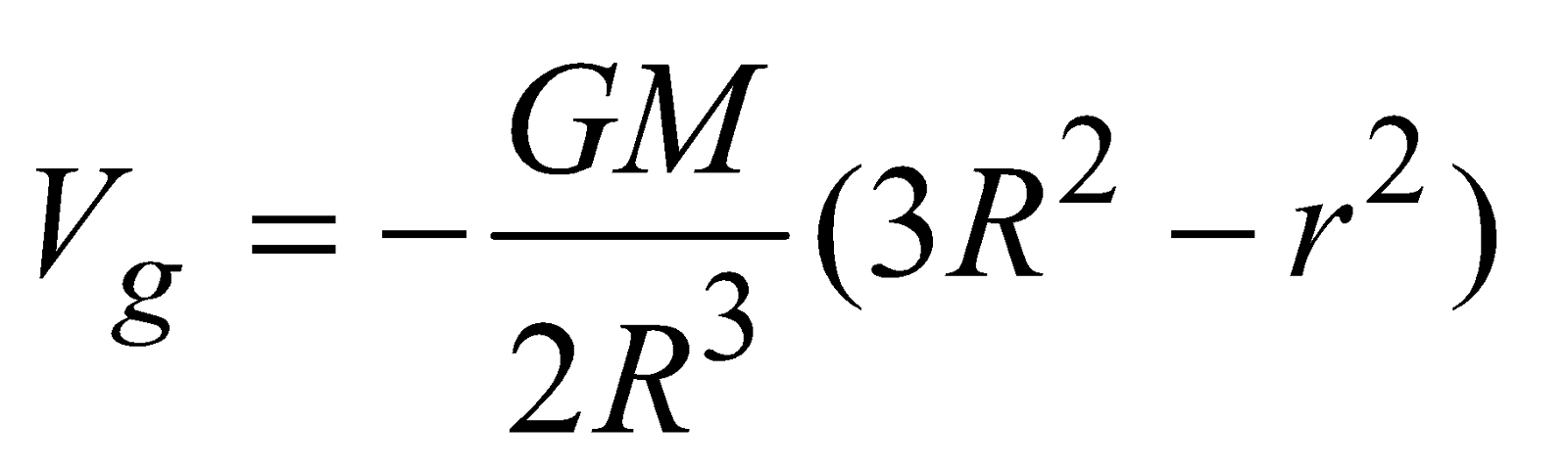 (r < R)
(r < R)
- Potential at the centre of solid sphere is
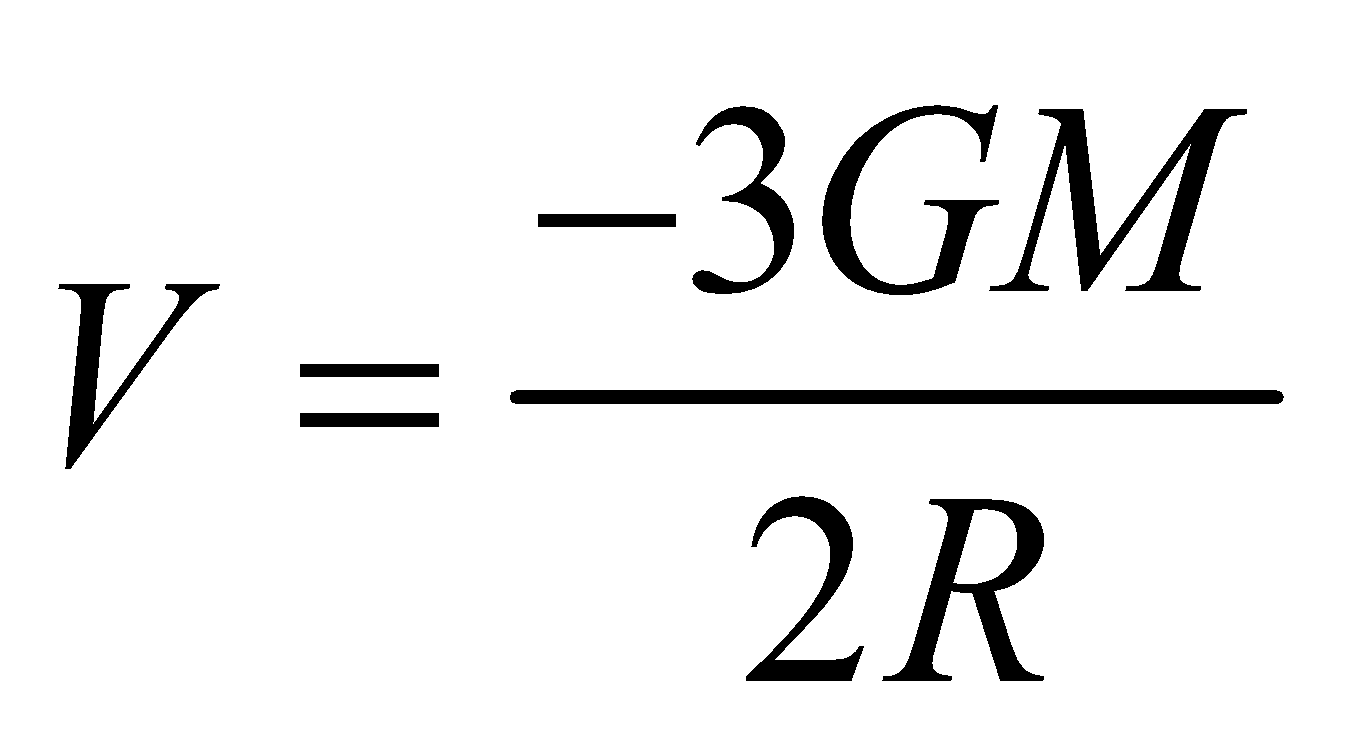
GRAVITATIONAL POTENTIAL ENERGY
- The gravitational potential energy of a mass m at a point above the surface of the earth at a height h is given by
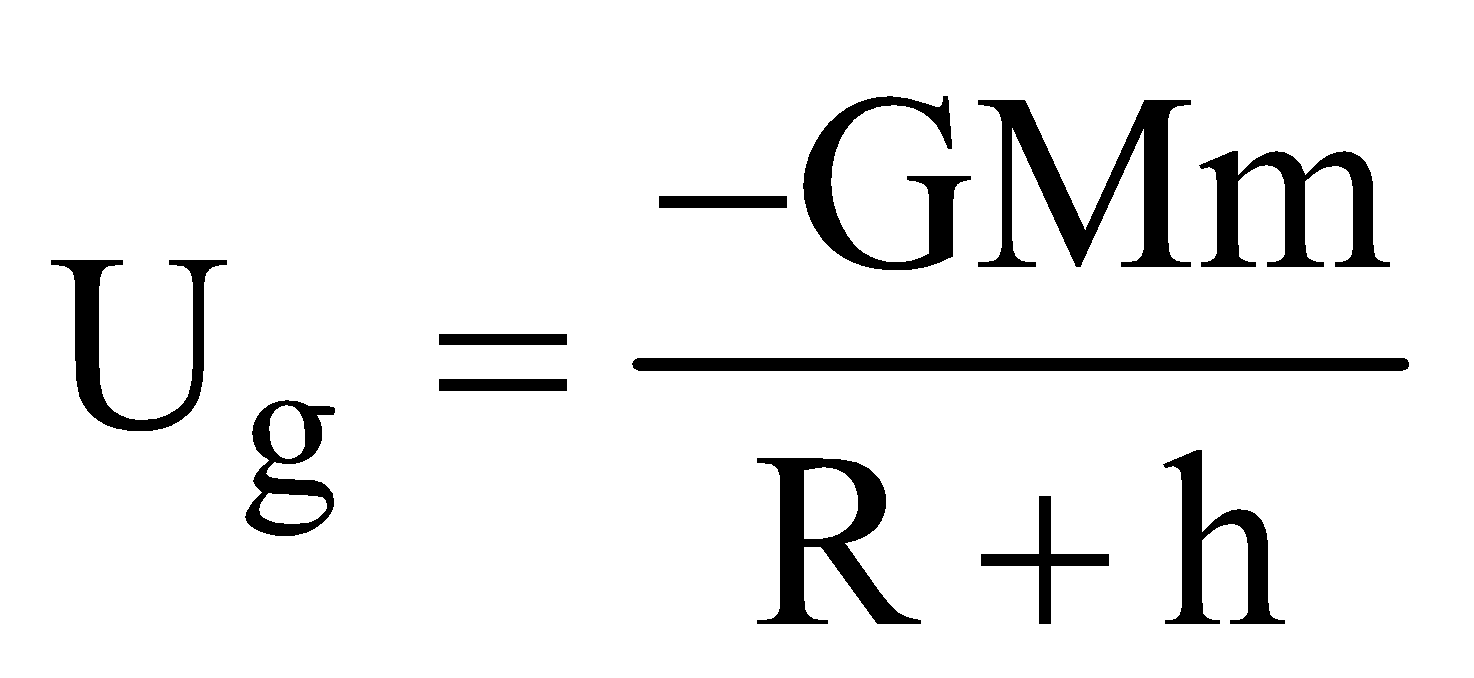 . The –ve sign shows that if h increases, the gravitational PE decreases and becomes zero at infinity.
. The –ve sign shows that if h increases, the gravitational PE decreases and becomes zero at infinity. - If we take reference level to be at the surface of earth (not at infinity) i.e., we assume that the gravitational P.E of a mass m is zero at the surface of earth, then the gravitational potential energy at a height h above the surface of earth is (mgh), where h << Re (radius of earth)
- The gravitational P.E of mass m on the earth’s surface is
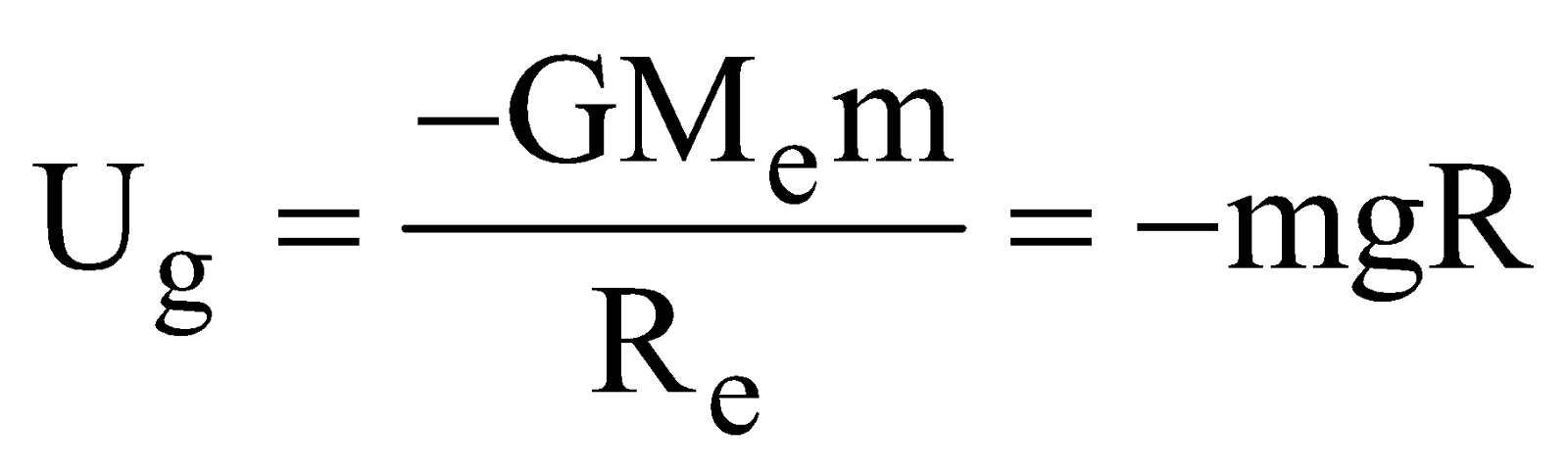
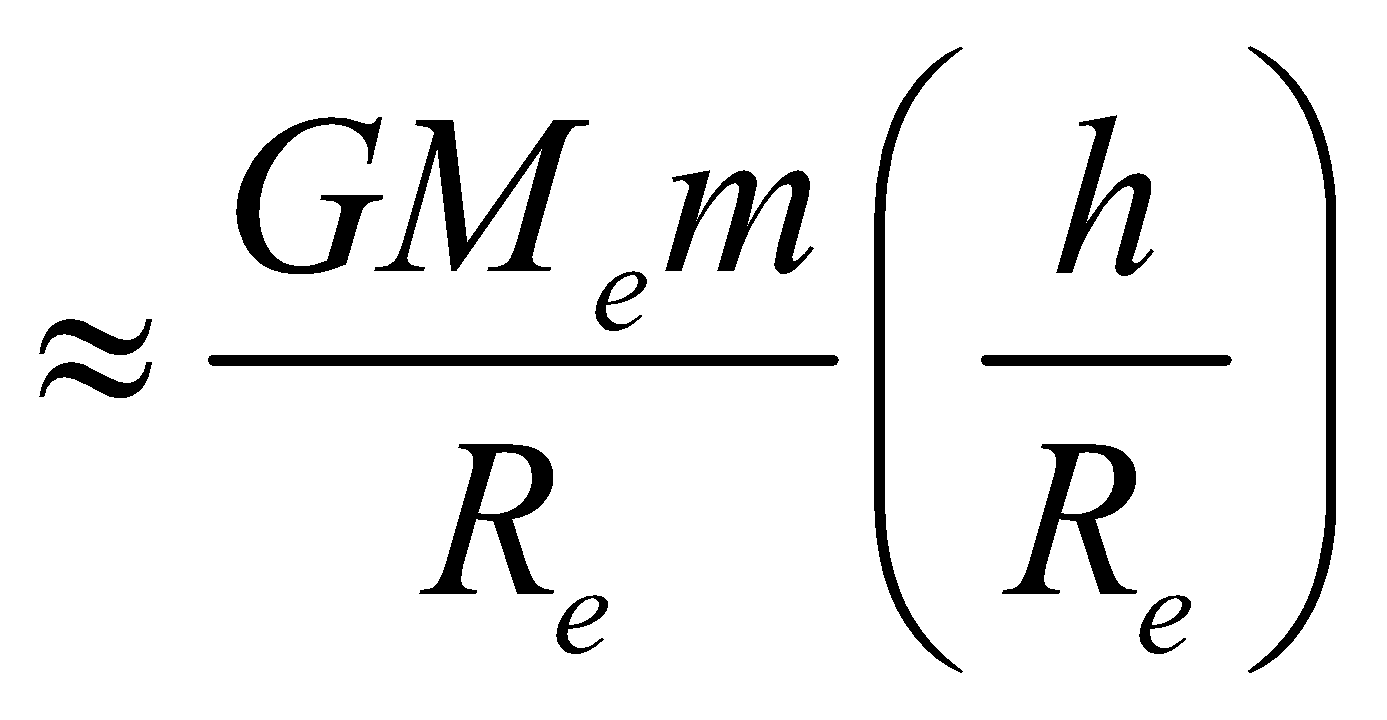 (if h<<R)
(if h<<R)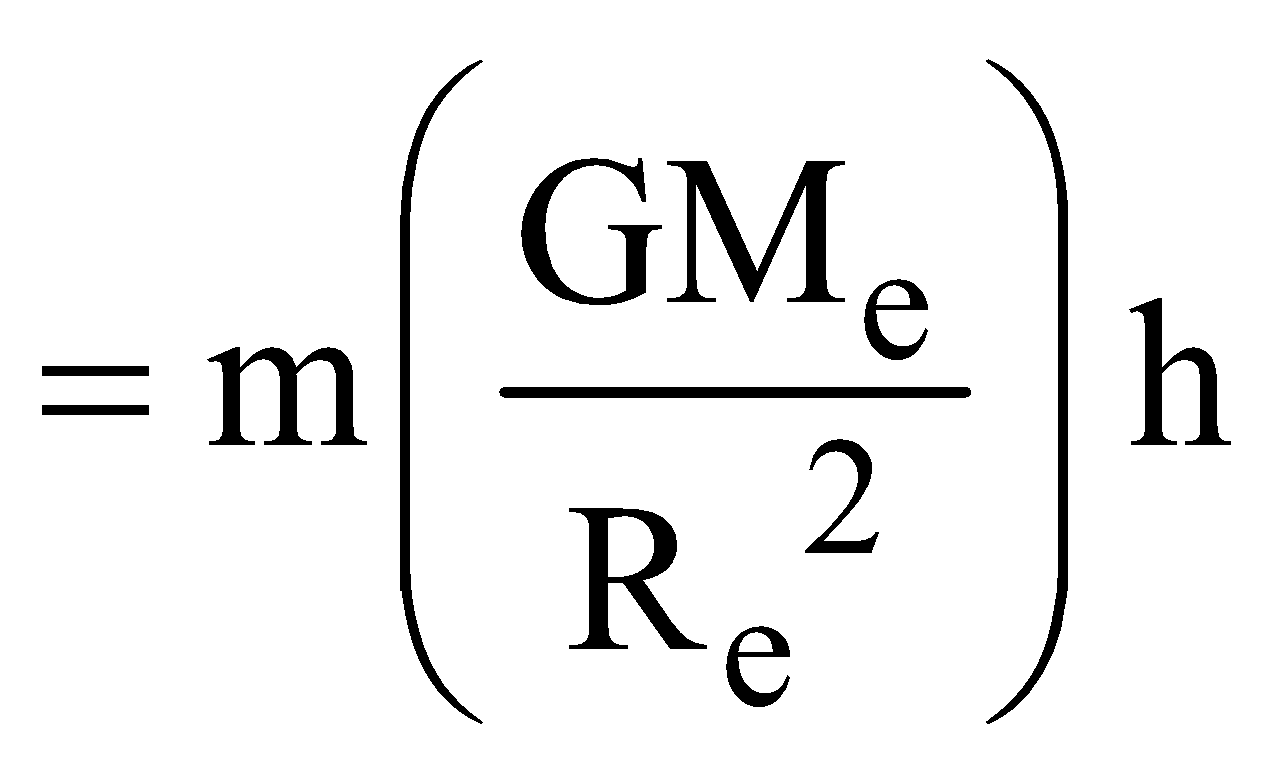
SATELLITES
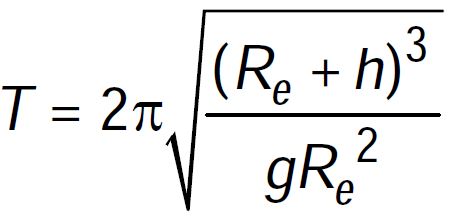
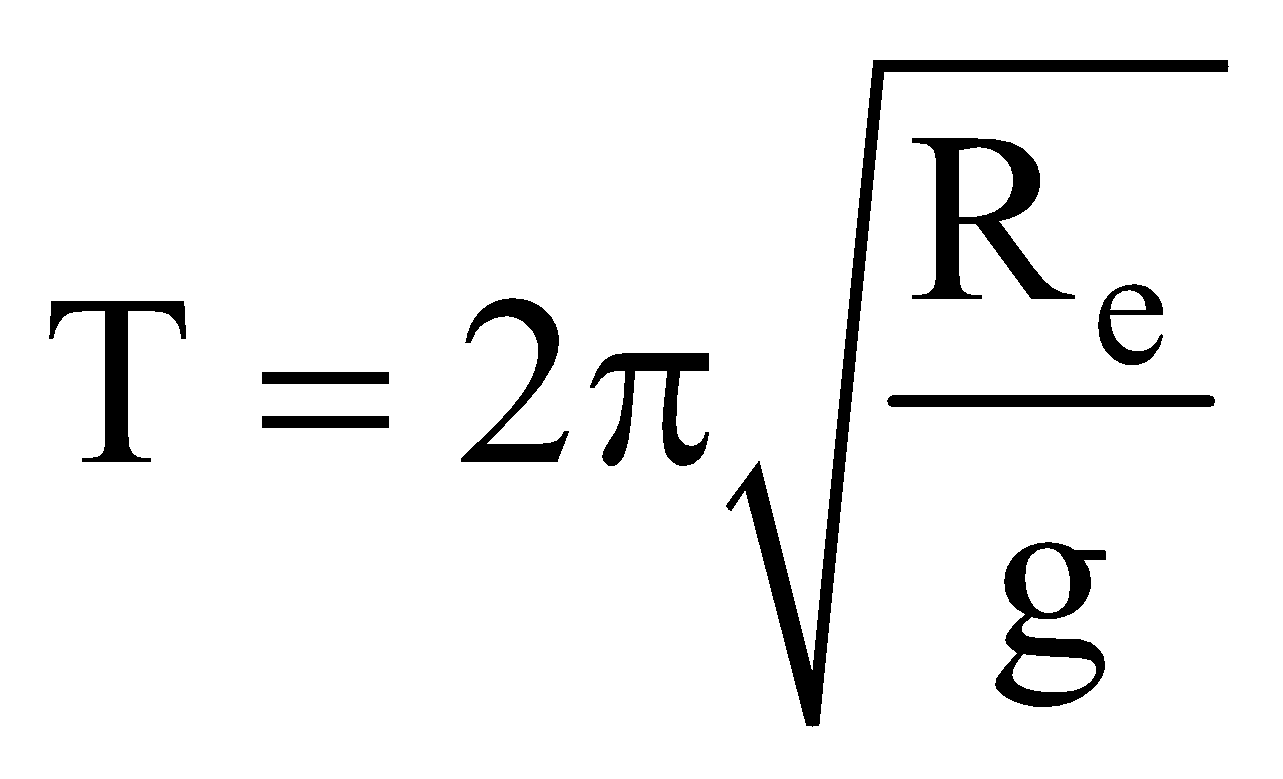 ; Re = 6.4 × 106 m ; g = 9.8 ms–2
; Re = 6.4 × 106 m ; g = 9.8 ms–2ORBITAL VELOCITY (V0 )
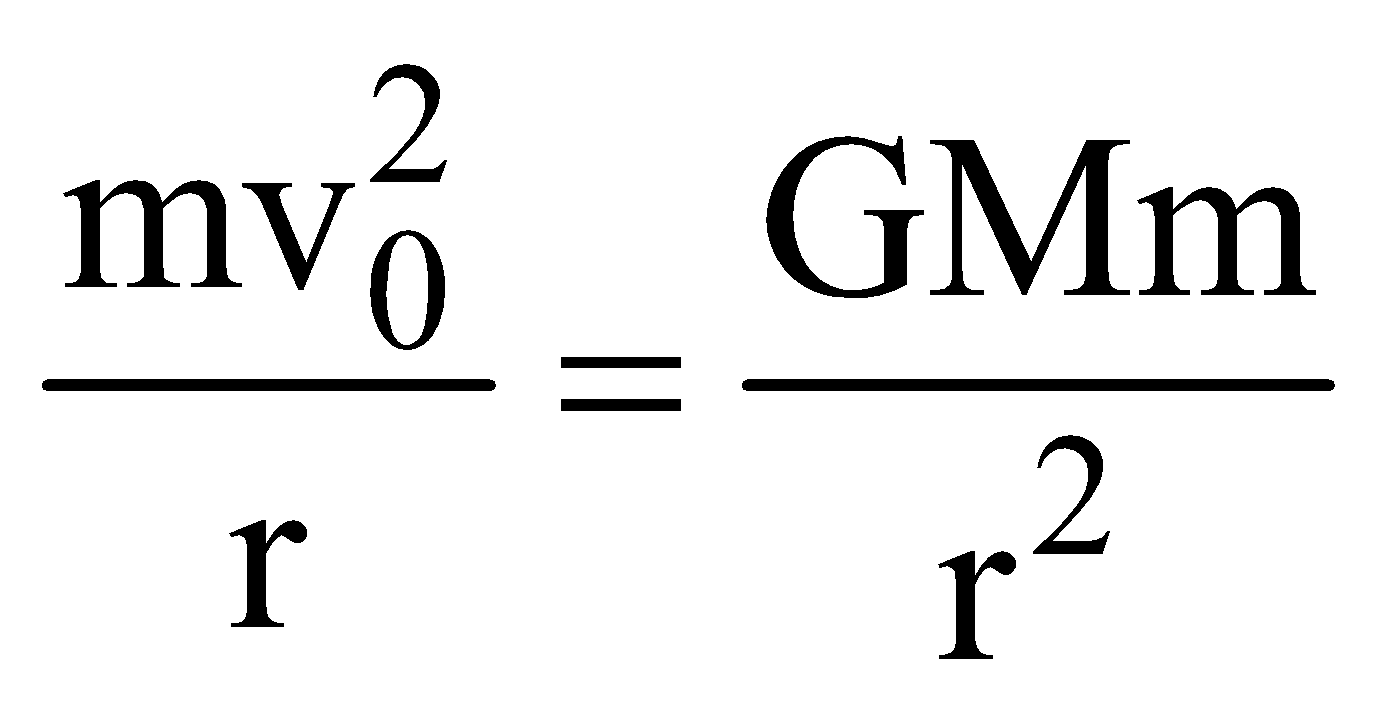 or
or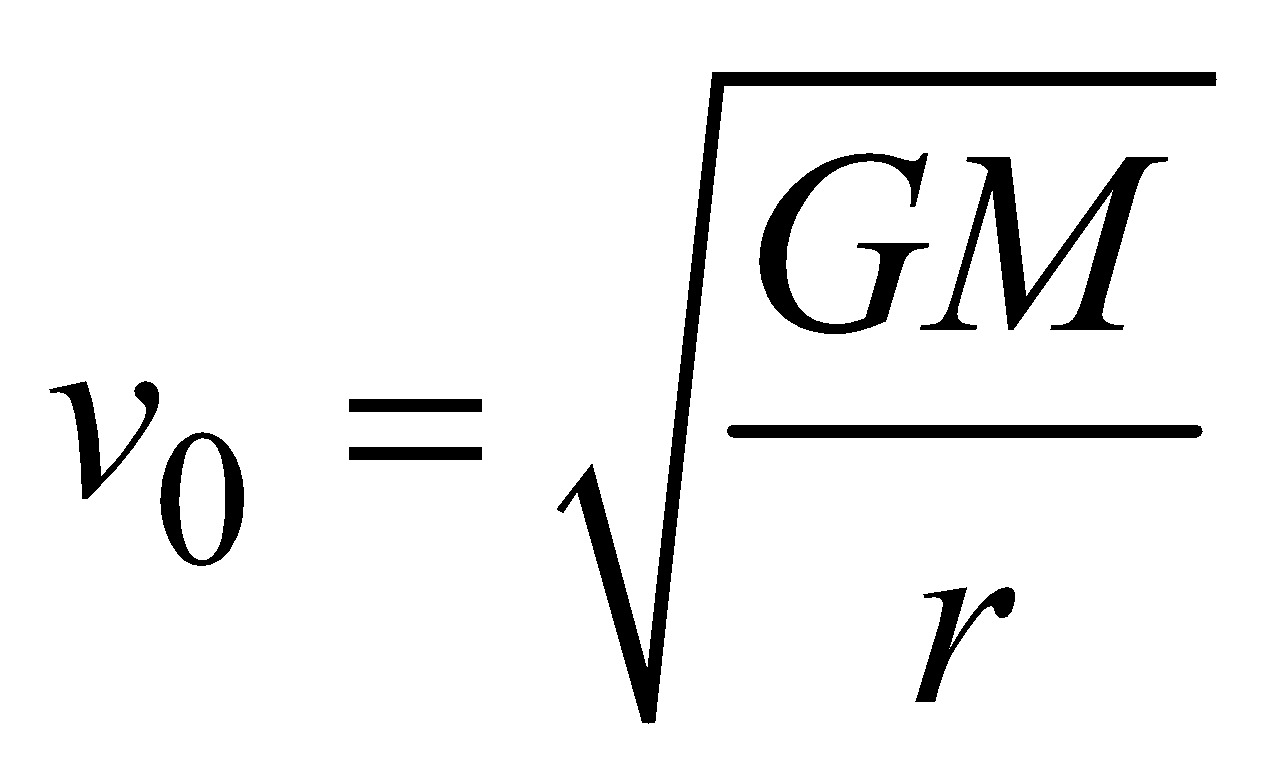 ………. (1)
………. (1)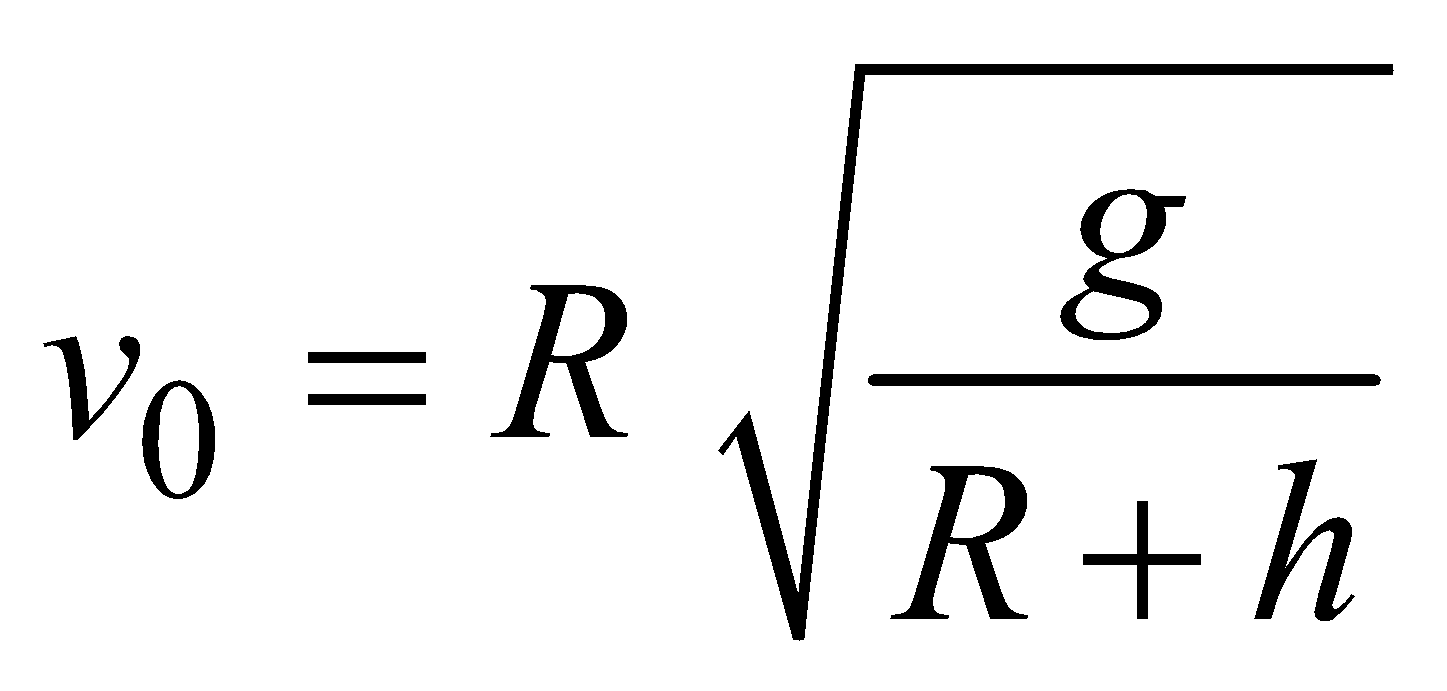 [∵
[∵ 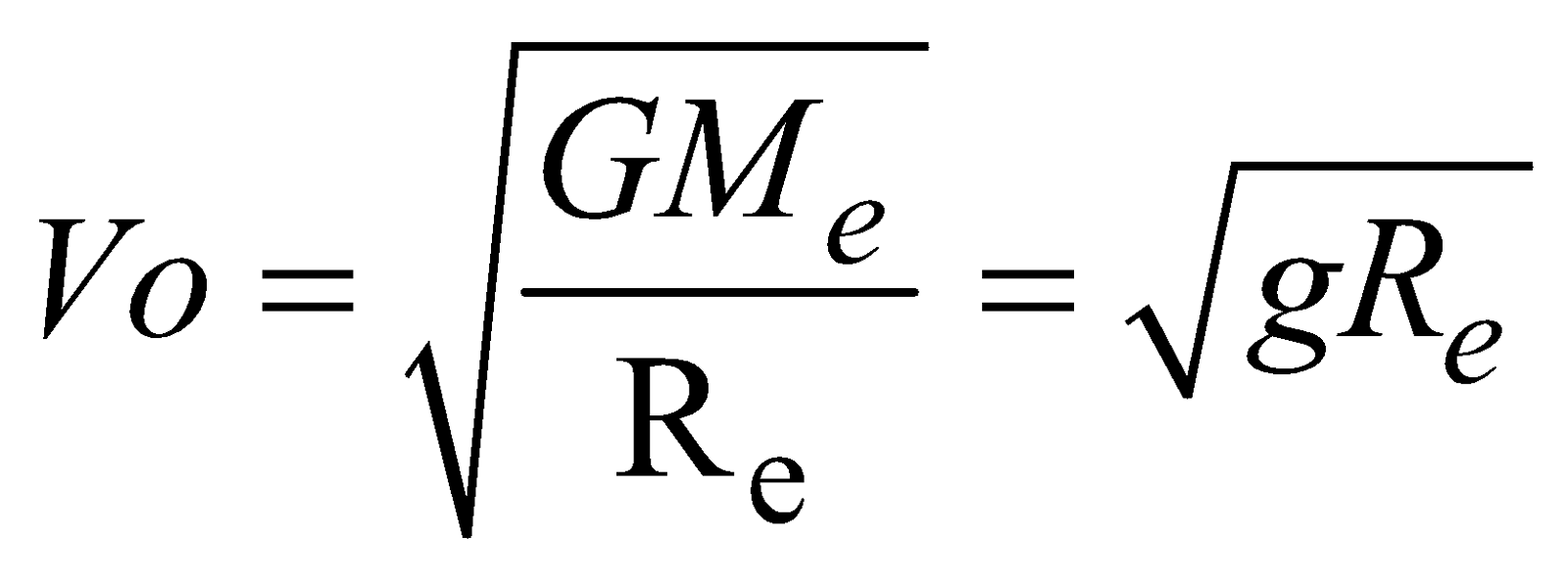
- Value of orbital velocity does not depend on the mass of the satellite.
- Around the earth the value of orbital velocity is 7.92 km/sec.
- Greater is the height of the satellite, smaller is the orbital velocity.
- The direction of orbital velocity is along the tangent to the path.
- The work done by the satellite in a complete orbit is zero.
ANGULAR MOMENTUM (L)
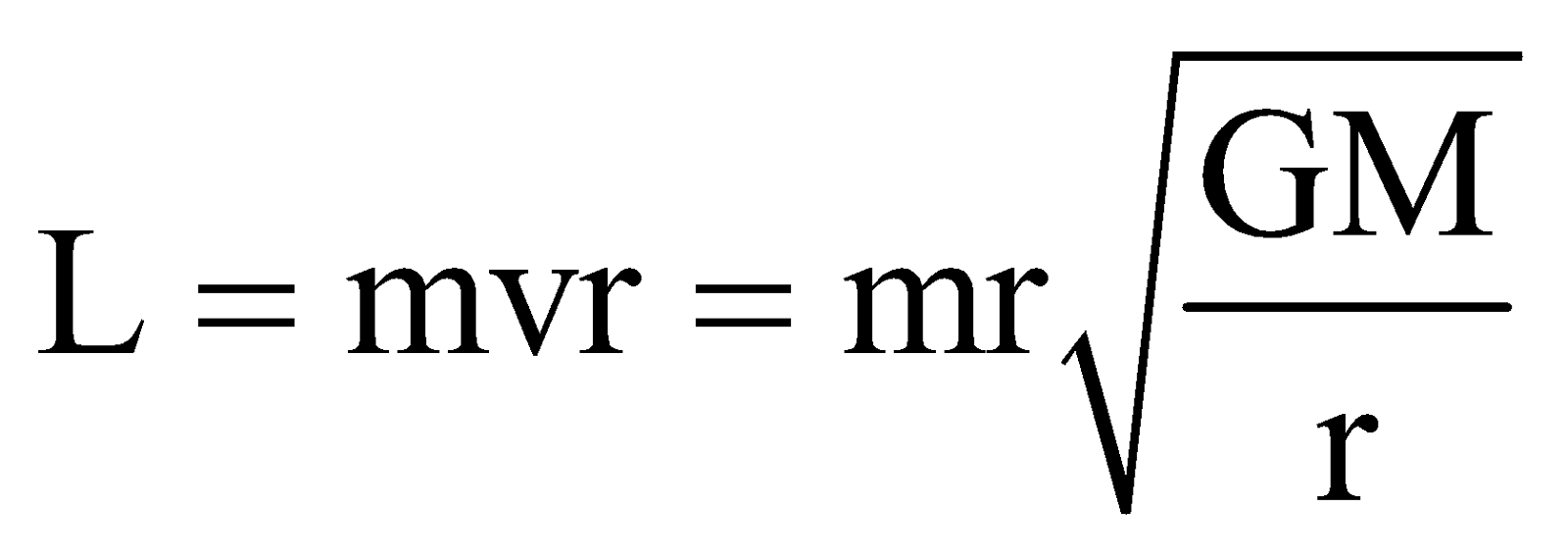
ENERGY OF A SATELLITE
- The gravitational potential energy of a satellite of mass m
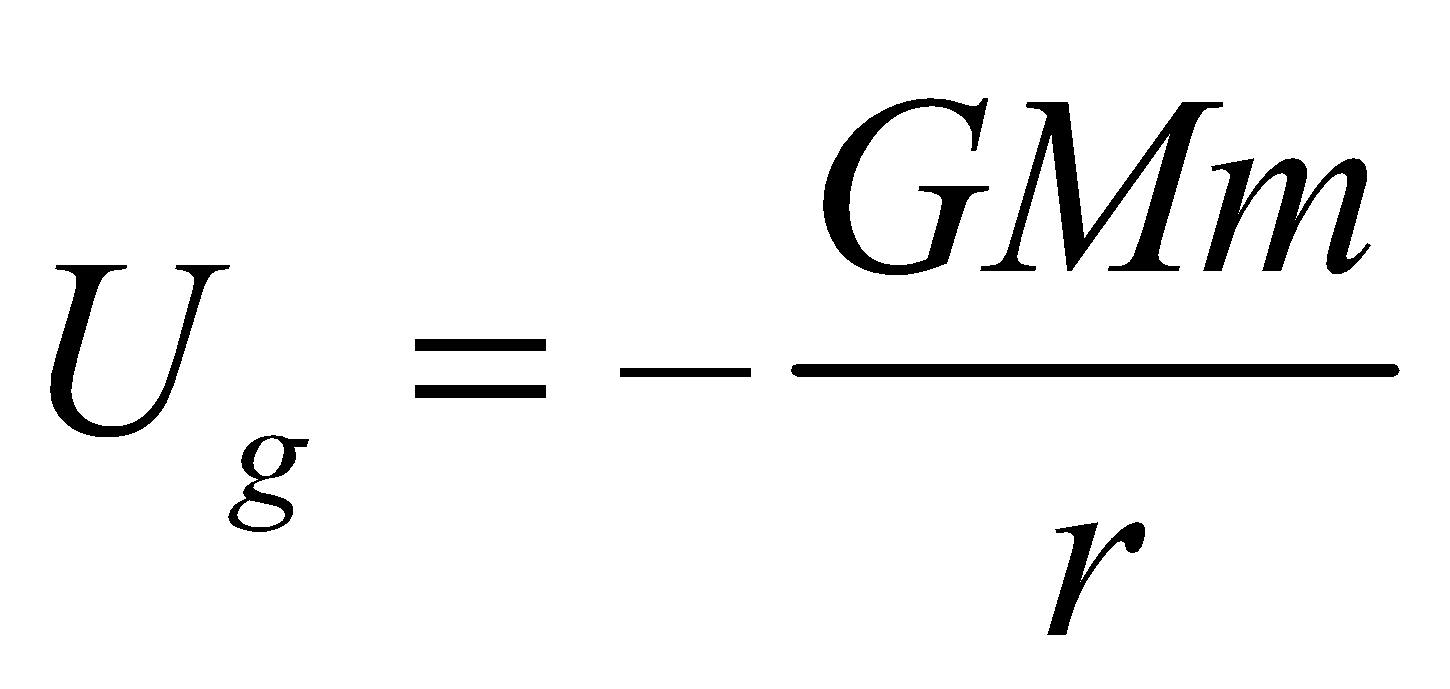 , where r is the radius of the orbit.
, where r is the radius of the orbit. - Kinetic energy of the satellite
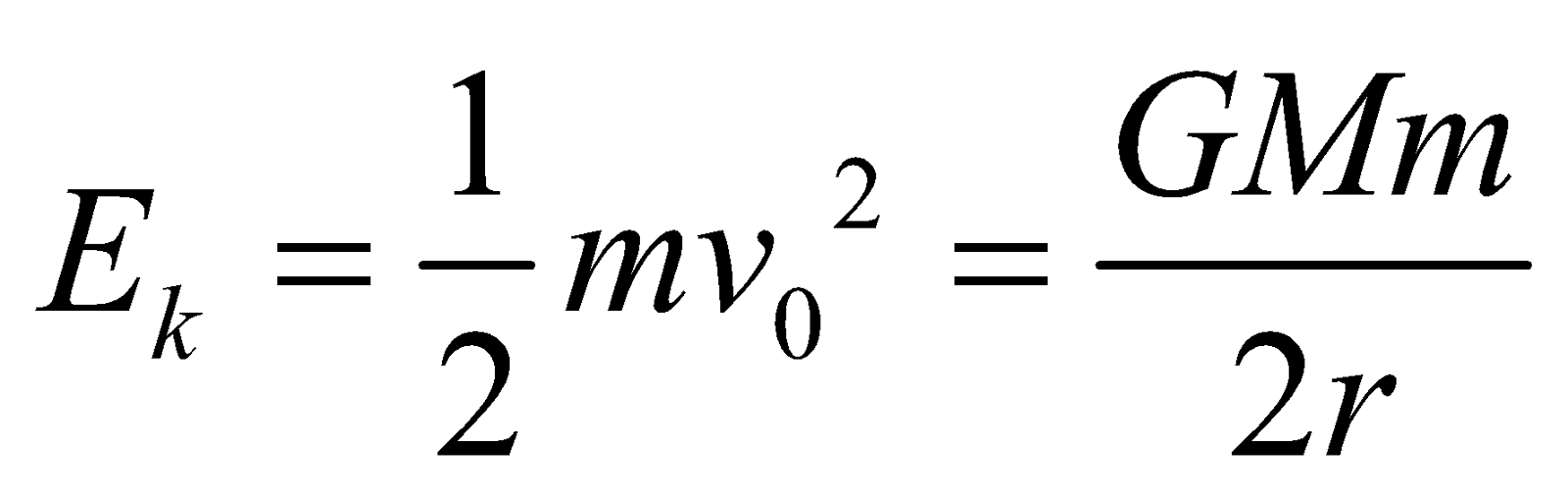
- So, total energy of the satellite
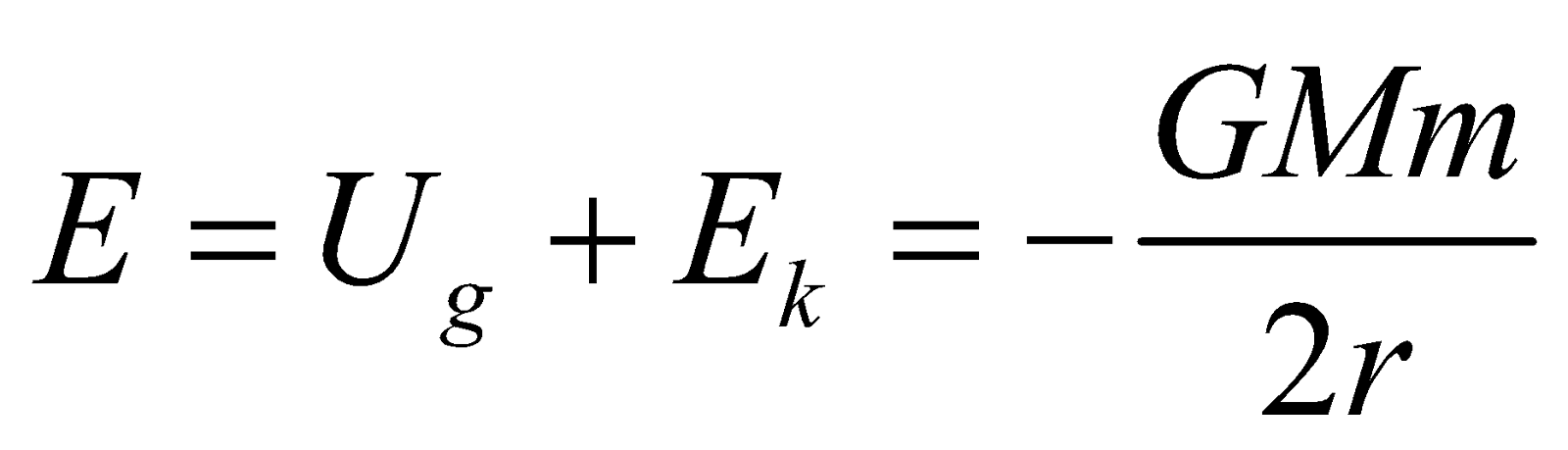
- Total energy of a satellite at a height equal to the radius of the earth
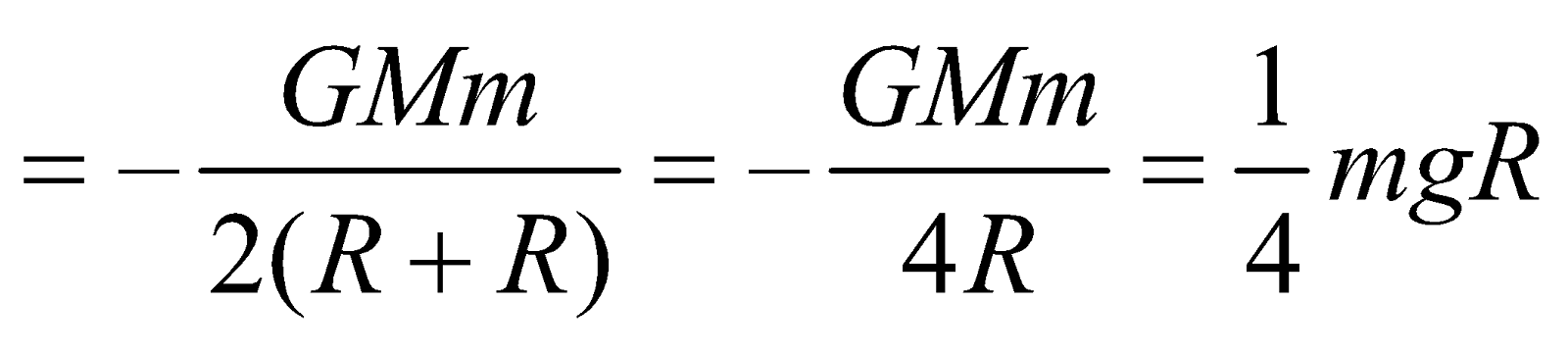
GEO-STATIONARY SATELLITE
- The orbit of the satellite must be circular and in the equatorial plane of the earth.
- The angular velocity of the satellite must be in the same direction as the angular velocity of rotation of the earth i.e., from west to east.
- The period of revolution of the satellite must be equal to the period of rotation of earth about its axis. i.e. 24 hours = 24 × 60 × 60 = 86400 sec.
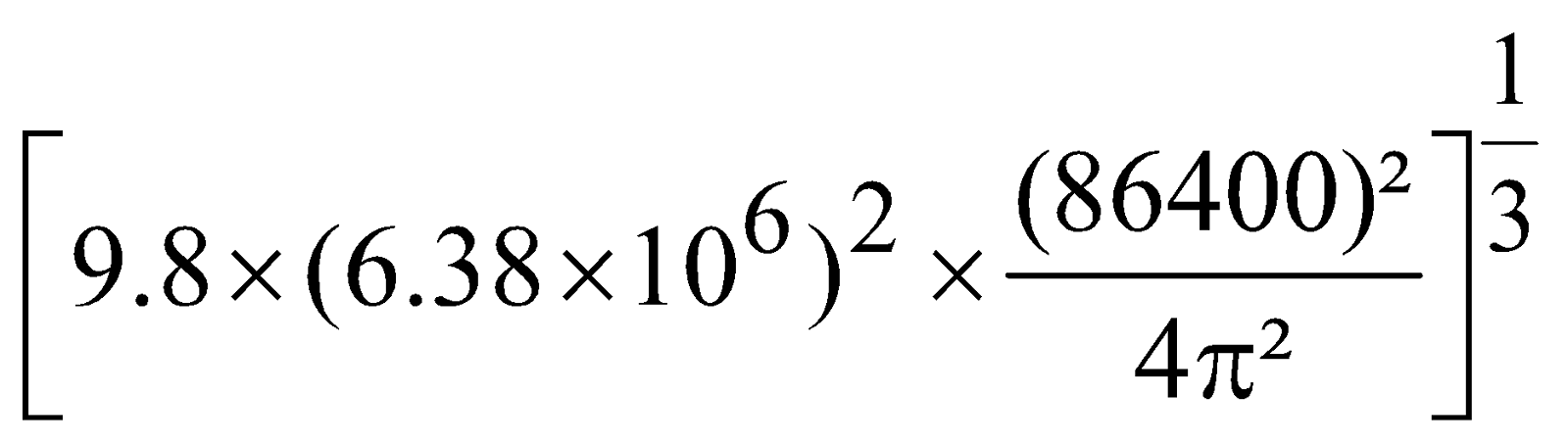
- Height of geostationary satellite from the surface of the earth is nearly 35600 km.
- The orbital velocity of this satellite is nearly 3.08 km/sec.
- The relative velocity of geostationary satellite with respect to earth is zero.
- This type of satellite is used for communication purposes. The orbit of a geostationary satellite is called ‘Parking Orbit’.
POLAR SATELLITE
- When v < v0
- The path is spiral. The satellite finally falls on the earth
- Kinetic energy is less than potential energy
- Total energy is negative
- When v = v0
- The path is circular
- Eccentricity is zero
- Kinetic energy is less than potential energy
- Total energy is negative
- When v0 < v < ve
- The path is elliptical
- Eccentricity < 1
- Kinetic energy is less than potential energy
- Total energy is negative
- When v = ve
- The path is a parabola
- Eccentricity = 1
- Kinetic energy is equal to potential energy
- Total energy is zero
- When v > ve
- The path is a hyperbola
- Eccentricity > 1
- Kinetic energy is greater than potential energy
- Total energy is positive
- The energy
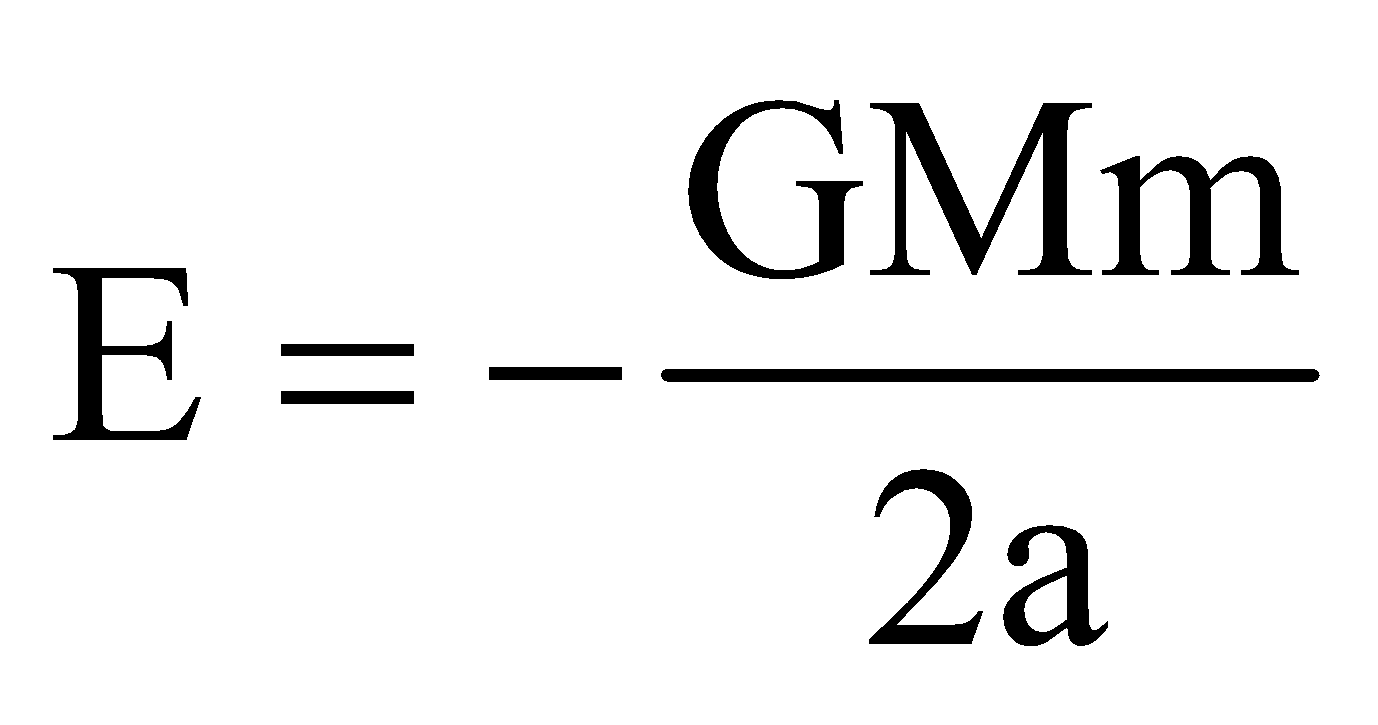 = const. with ‘a’ as semi-major axis;
= const. with ‘a’ as semi-major axis; - KE will be maximum when the satellite is closest to the central body (at perigee) and minimum when it is farthest from the central body (at apogee) [as for a given orbit L = const.,
i.e., mvr = const., i.e., v ∝ 1/r] - PE = (E – KE) will be minimum when KE = max, i.e., the satellite is closest to the central body (at perigee) and maximum when KE = min, i.e., the satellite is farthest from the central body (at apogee).
ESCAPE SPEED (Ve)
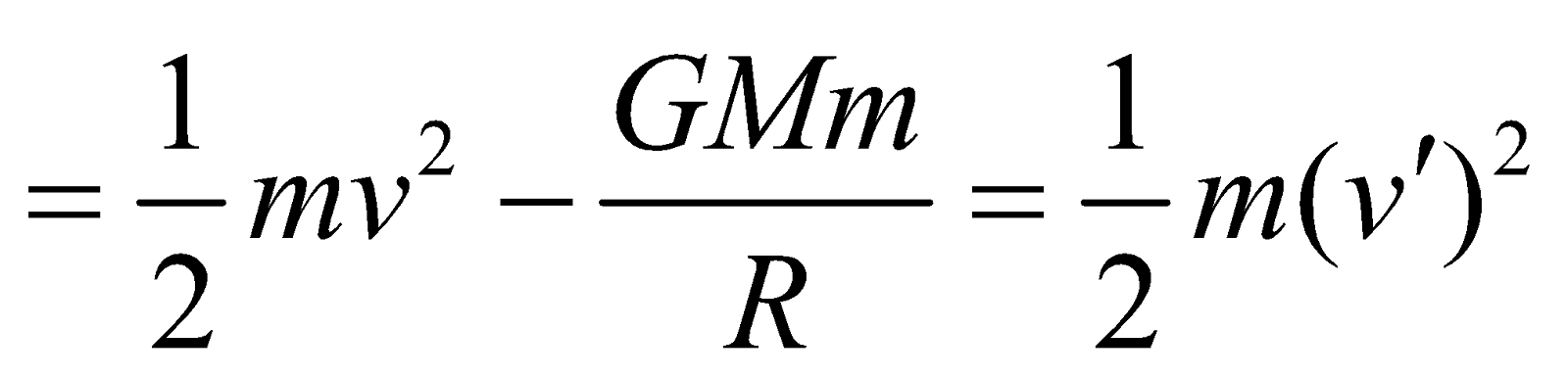
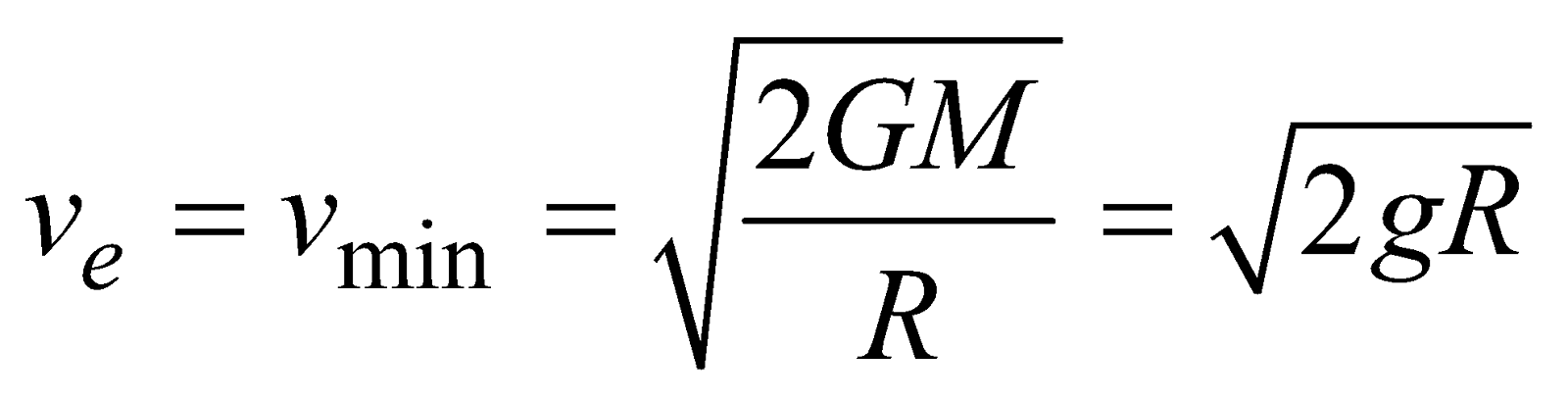
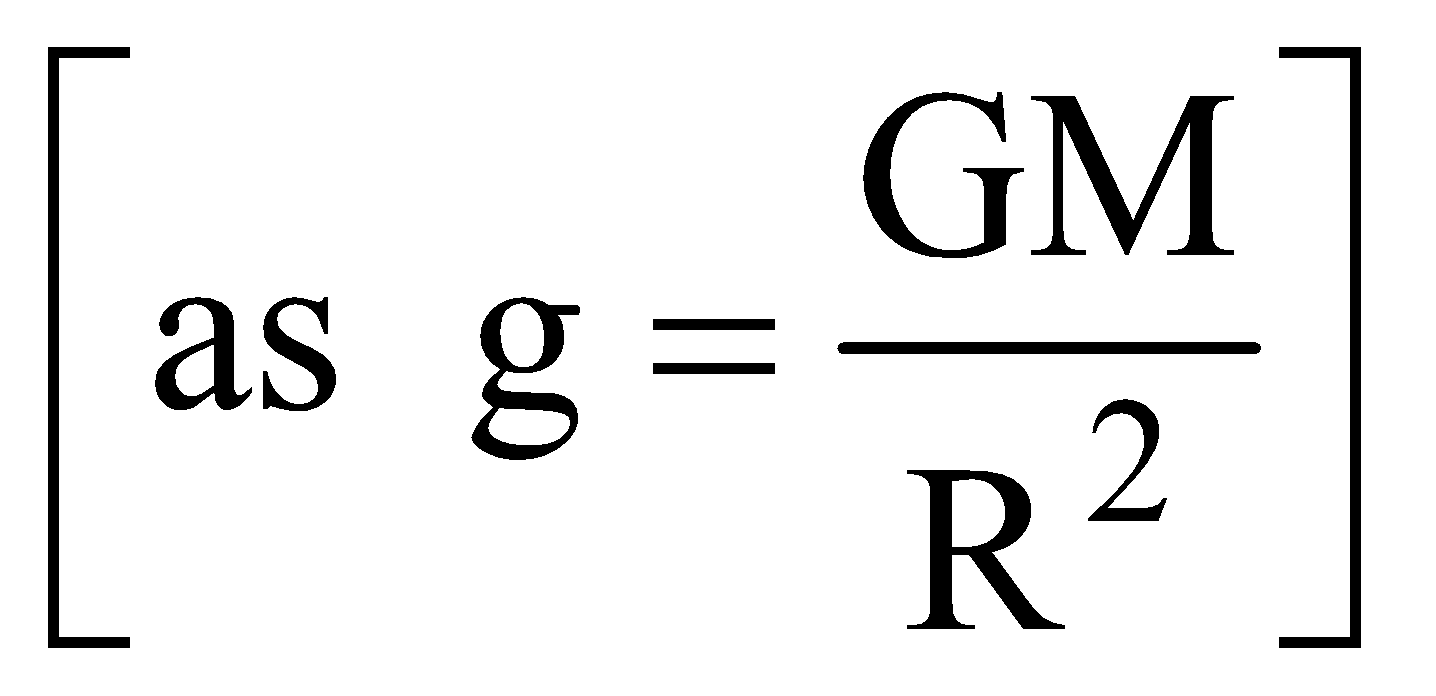
- The value of escape velocity does not depend upon the mass of the projected body, instead it depends on the mass and radius of the planet from which it is being projected.
- The value of escape velocity does not depend on the angle and direction of projection.
- The value of escape velocity from the surface of the earth is 11.2 km/sec.
- The minimum energy needed for escape is = GMm/R.
- If the velocity of a satellite orbiting near the surface of the earth is increased by 41.4%, then it will escape away from the gravitational field of the earth.
- If a body falls freely from infinite distance, then it will reach the surface of earth with a velocity of 11.2 km/sec.
- The escape velocity on moon is low as (as gm=gE/6) hence there is no atmosphere on moon.
- If the orbital radius of the earth around the sun be one fourth of the present value, then the duration of the year will be one eighth of the present value.
- The satellites revolve around the earth in a plane that coincides with the great circle around the earth.
KEPLER’S LAWS OF PLANETARY MOTION
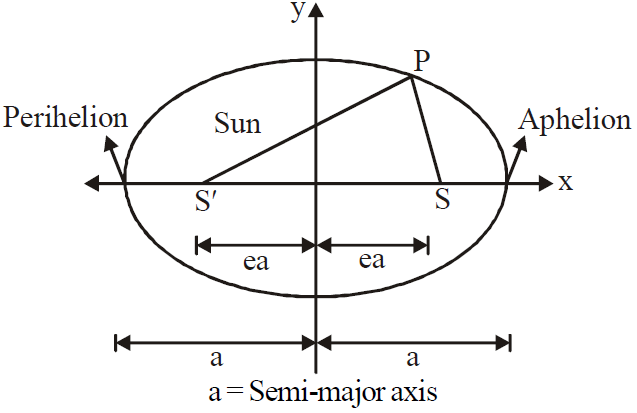
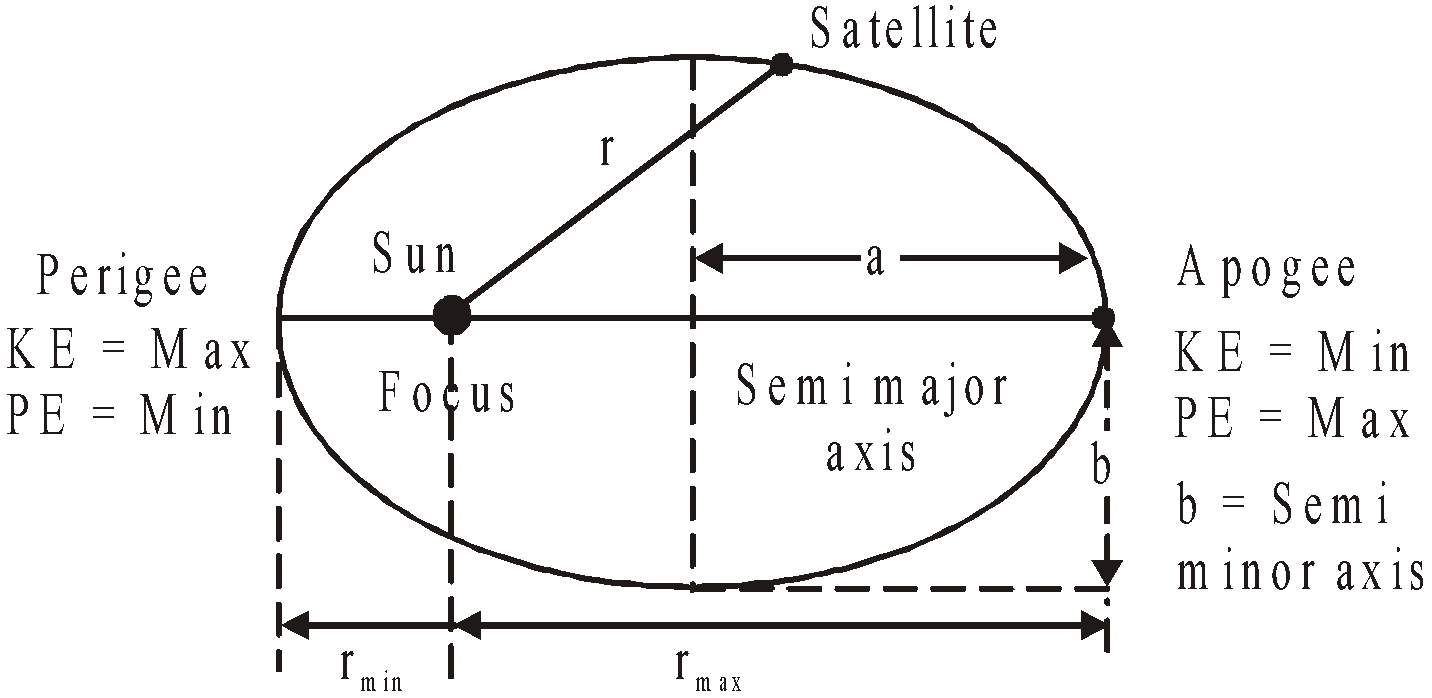
LAW OF ORBITS
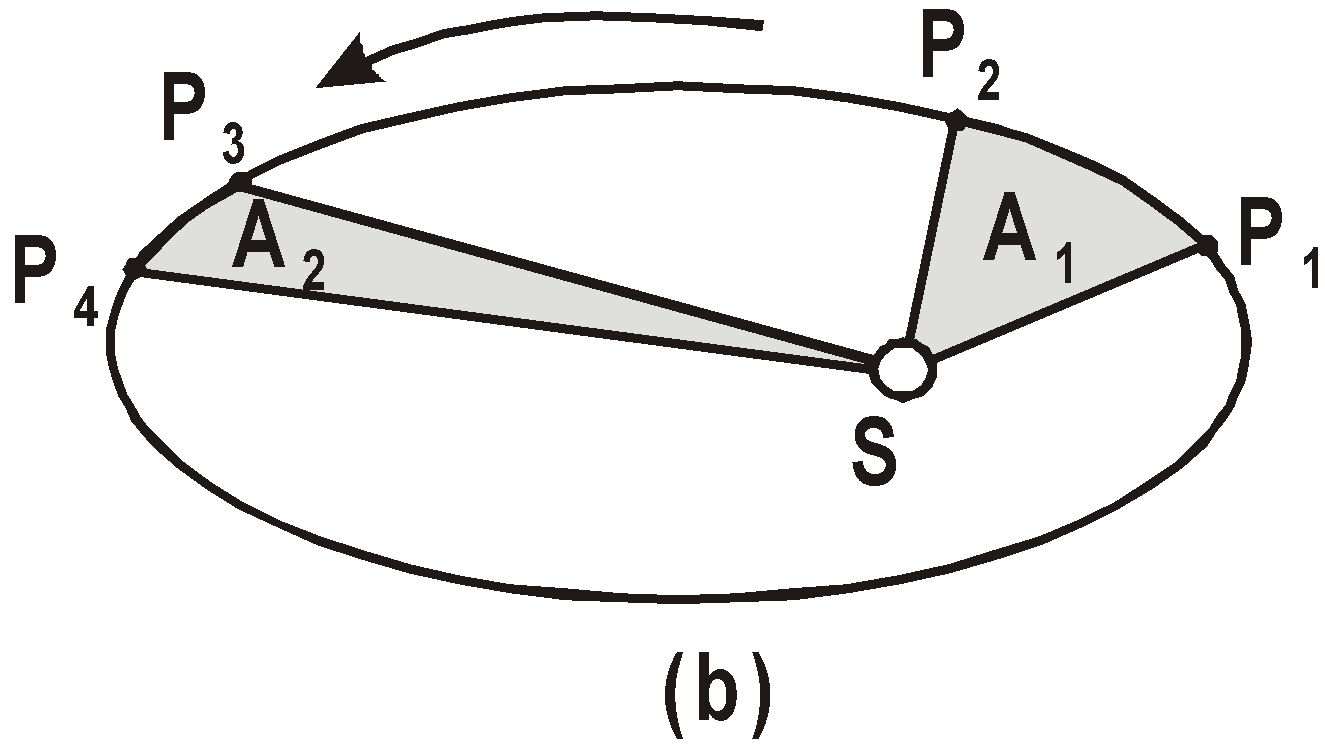
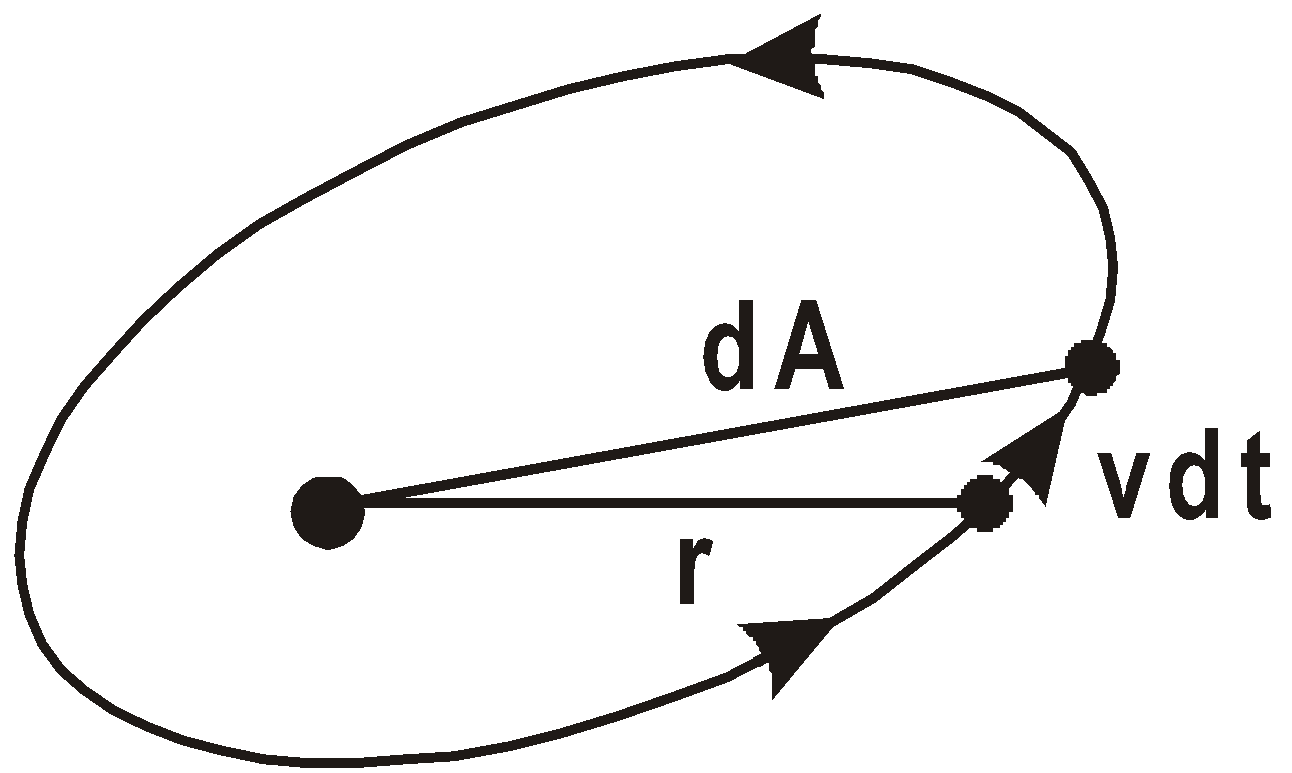
LAW OF AREAS
LAW OF PERIODS
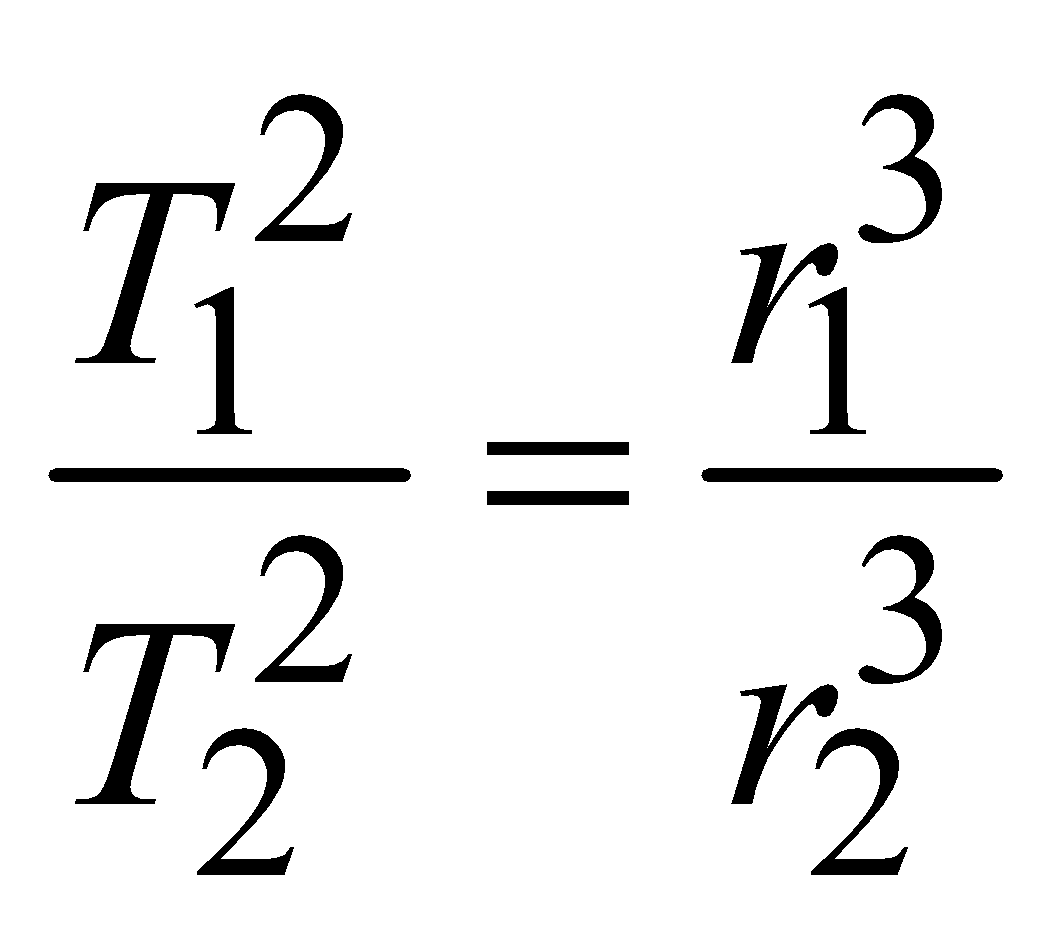
WEIGHTLESSNESS

- The moon takes 27.3 days to revolve around the earth.
The radius of its orbit is 3.85 × 105 km. - Kepler’s second law is based on conservation of angular momentum.
- Perihelion distance is the shortest distance between the sun and the planet.
- Aphelion distance is the largest distance between the Sun and the planet.
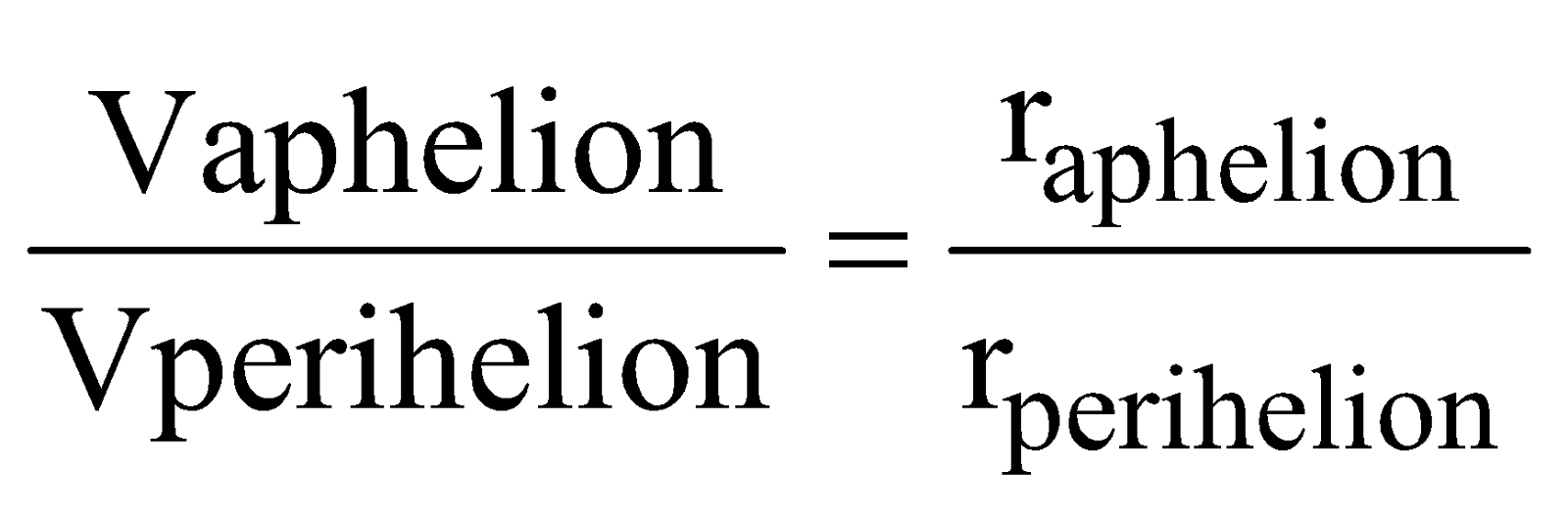
- If e is the eccentricity of the orbit
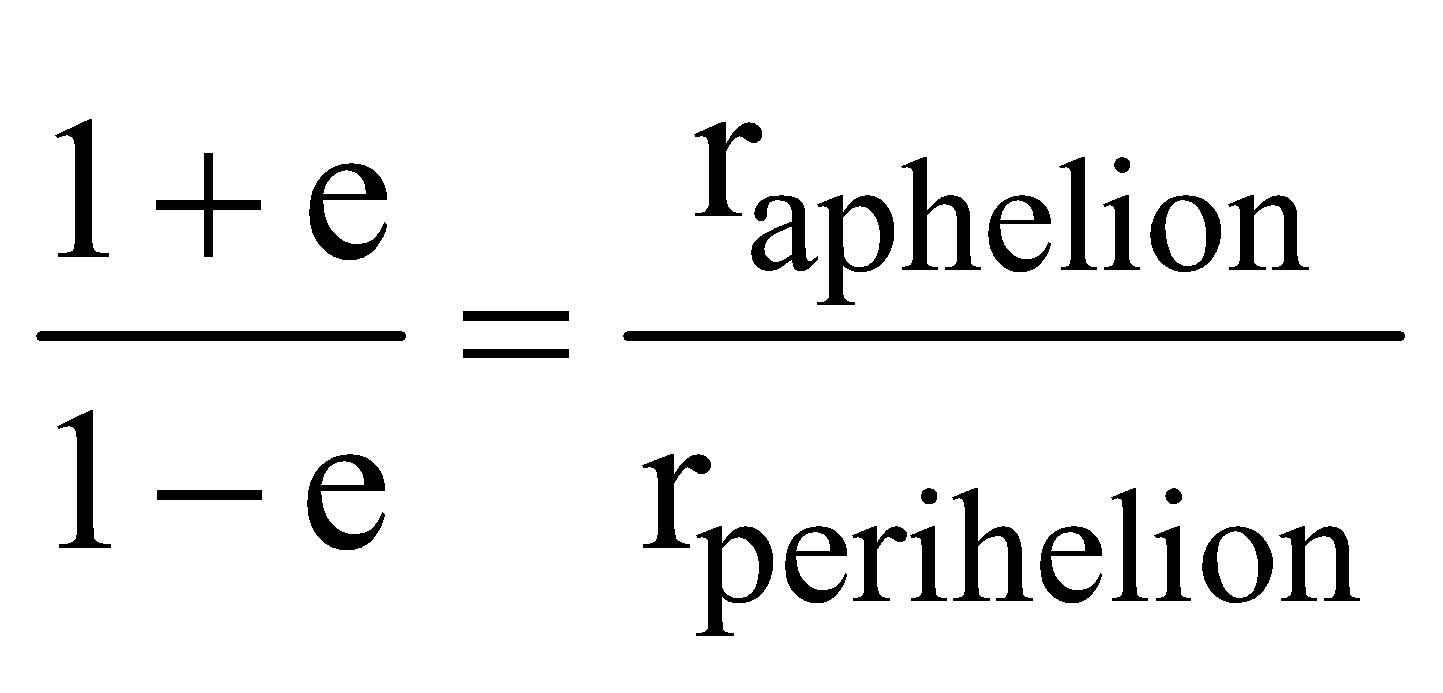
- If e > 1 and total energy (KE + PE) > 0, the path of the satellite is hyperbolic and it escapes from its orbit.
- If e < 1 and total energy is negative it moves in elliptical path.
- If e = 0 and total energy is negative it moves in circular path.
- If e = 0 and total energy is zero it will take parabolic path.
- The path of the projectiles thrown to lower heights is parabolic and thrown to greater heights is elliptical.
- Kepler’s laws may be applied to natural and artificial satellites as well.
- Gravitational force does not depend upon medium so no medium can shield it or block it.
- The escape velocity and the orbital velocity are independent of the mass of the body being escaped or put into the orbit.