Question
(a) The cost,\( $C\), of a party for n people is calculated using the following formula.
C = 130 + 4n
(i) Calculate C when n = 25.
(ii) Eurdley has a party which costs \($1138.\)
How many people is this party for?
(b) Solve the following equations.
(i) 3x = 27
(ii) 8y – 4 = 24
(iii) 4(5q – 2) = 72
(c) Solve the simultaneous equations.
6x + 8y = –31
14x – 5y = 46
Answer/Explanation
Answer:
(a) (i) 230
(ii) 252
(b) (i) 9
(ii) 3.5
(iii) 4
(c) x = 1.5 or 3/2
y = –5
Question
(a) In 2001 Arnold was x years old.
Ken is 34 years younger than Arnold.
(i) Complete the table, in terms of x, for Arnold’s and Ken’s ages.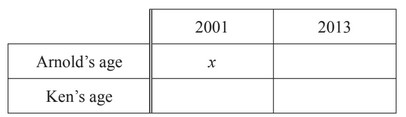
(ii) In 2013 Arnold is three times as old as Ken.
Write down an equation in x and solve it.
(b) Solve the simultaneous equations.
3x + 2y = 18
2x – y = 19
Answer/Explanation
Answer:
(a) (i) x +12
x – 34 x − 22
(ii) x +12 = 3(x – 22)
39 cao
(e)
8
-3
Question
(a) Solve these equations.
(i) x + 7 = 15
x = ………………………………………….
(ii) 5(3x + 8) = 10
x = ………………………………………….
(b) A club is arranging transport for its members.
Speedy Coaches charge $625 plus $15 per member.
The total cost, in dollars, for x members is given by the expression 15x + 625.
(i) Sporty Coaches charge $117 plus $19 per member.
Write an expression for the total cost, in dollars, for x members.
(ii) The total cost is the same for both Speedy Coaches and Sporty Coaches.
Write down an equation and solve it to find x.
Answer/Explanation
Answer:
(a) (i) 8
(ii) -2
(b) (i) 19x + 117
(ii) 15x + 625 = their (b) (i)
127
