Question
Use your calculator to work out
\(\frac{8.2^2-52.48}{7.38-6.18}\)
▶️Answer/Explanation
Using a calculator, the expression \(\frac{8.2^2-52.48}{7.38-6.18}\) can be calculated as follows:
\(\frac{8.2^2-52.48}{7.38-6.18} = \frac{67.24-52.48}{1.2} = \frac{14.76}{1.2} = 12.3\)
Therefore, the result is 12.3.
Question
(a) Calculate \(\sqrt{2.3+6.4^{2}}\), writing down your full calculator display.
……………………………………….
(b) Write your answer to part (a) correct to 4 decimal places.
……………………………………….
▶️Answer/Explanation
(a) The calculator display would show:
\(\sqrt{2.3+6.4^{2}} = \sqrt{2.3+40.96} = \sqrt{43.26}\)
\(\sqrt{43.26} \approx 6.583314\)
(b) Rounding the result to 4 decimal places, we have:
\(\sqrt{2.3+6.4^{2}} \approx 6.5833\)
Therefore, the correct answer to part (b) is 6.5833, correct to 4 decimal places.
Question
(a) Calculate \(\sqrt[3]{-4.3\times 6.7^{2}}\) and write down all the figures shown on your calculator.
(b) Write your answer to part (a) correct to 4 decimal places.
▶️Answer/Explanation
(a) To calculate \(\sqrt[3]{-4.3\times 6.7^{2}}\):
Calculate \(6.7^{2}\):
\(6.7 \times 6.7 = 44.89\)
\(-4.3 \times 44.89 = -193.927\)
\(\sqrt[3]{-193.927} \approx -5.779266\)
(b) To write the answer correct to 4 decimal places, we round the result from part (a) to four decimal places:
\(-5.7793\) (rounded to four decimal places)
Question
This is Edha’s method to work out\( 99\times 27 \) without using a calculator.
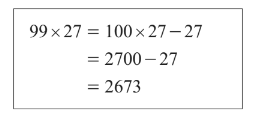
Show how to use Edha’s method to work out \(99\times 68\) without using a calculator.
▶️Answer/Explanation
100× 68 -68
= − 6800 -68
= 6732
