Question
(a) Work out \(48\div 3-5\times 2\).[1]
(b) Insert one pair of brackets to make this statement correct.
3 + 2 x 12 – 4 = 19 [1]
(c) Write the following in order, starting with the smallest.
\(\frac{3}{4}\) 0.749 76%
……………….. 1 ……………….. 1 ……………….. 1 ……………….. [2]
smallest
(d) Find the value of
(i) \(\sqrt{265.69}\),[1]
(ii) 83.[1]
(e) Write down the smallest prime number. [1]
(f) Write down all the factors of 18.[2]
(g) Write down a common factor of 16 and 72 that is greater than 2.[1]
(h) Write \(\frac{28}{140}\) as a fraction in its simplest form.[1]
(i) Jeff and his friends win a prize.
Jeff’s share is $160 which is \(\frac{5}{11}\) of the prize.
Work out the value of the prize.
\($\)[2]
Answer/Explanation
Ans:
2(a) 6
2(b) 3 + 2 × (12 – 4) = 19
2(c) \(\frac{11}{15}\) \(\left [ 0 \right ].749\) \(\frac{3}{4}\) 76[%]
2(d)(i) 16.3
2(d)(ii) 512
2(e) 2
2(f) 1 2 3 6 9 18
2(g) 4 or 8
2(h) \(\frac{1}{5}\) cao
2(i) 352
Question
(a) Write one hundred and twenty thousand and twenty in figures.
………………………………………….
(b) Find the value of\( \sqrt{3481}.\)
………………………………………….
(c)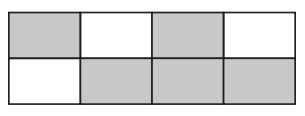
(i) Write down the fraction of the rectangle that is shaded.
………………………………………….
(ii) Find the percentage of the rectangle that is not shaded.
……………………………………….%
(d) Write these numbers in order, starting with the smallest.
27% \( \frac{5}{17}\) 0.268 \(\frac{7}{29}\)
……………….. <……………….. <……………….. <………………..
(e) Write 0.3728 correct to 1 decimal place.
…………………………………………
(f) Write down the value of \(19^{\circ}\)
…………………………………………..
(g) The height, h metres, of a tower is 128m, correct to the nearest metre.
Complete the statement about the value of h.
\(……………… \leq h< ………………\)
(h) Find the highest common factor (HCF) of 126 and 180.
………………………………………….
(i) Write down an irrational number with a value between 6 and 7.
………………………………………….
Answer/Explanation
(a) 120 020
(b) 59
(c)(i)\(\frac{5}{8}\)
(ii) 37.5
(d) \(\frac{7}{29}\) 0.268 27% \( \frac{5}{17}\)
(e) 0.4
(f) 1
(g) 127.5 128.5
(h) 18
(i) Any irrational number between 6 and 7
