Question
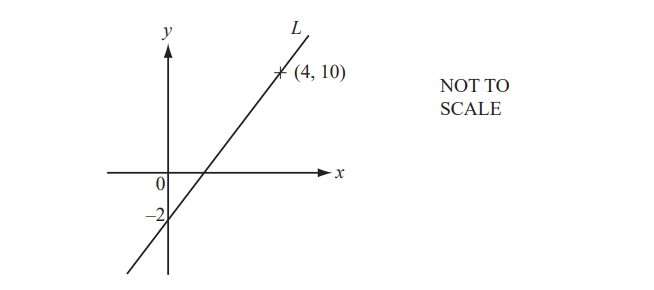
Line L passes through the point (4, 10).
(a) Find the gradient of line L.
(b) Write down the equation of line L, in the form y = mx + c.
(c) Line P passes through the point (0, 0).
Line P is parallel to line L.
Write down the equation of line P.
▶️Answer/Explanation
(a) To find the gradient of line L, we can use the formula:
Gradient (m) = (change in y) / (change in x)
We have the coordinates (4, 10) and (0, -2) on line L. The change in y is -2 – 10 = -12, and the change in x is 0 – 4 = -4. Therefore, the gradient of line L is:
\(m=\frac{-12}{-4}=3\)
(b) To write down the equation of line L in the form y = mx + c, we need to determine the y-intercept, c.
We know that line L passes through the point (4, 10). Substituting these values into the equation, we get:
10 = 3\times 4 + c
10 = 12 + c
c = 10 – 12 = -2
Therefore, the equation of line L is:zy = 3x – 2
(c) Line P is parallel to line L and passes through the point (0, 0). Since line P is parallel to line L, it will have the same gradient, which is 3. Therefore, the equation of line P is:
y = 3x
Question
(a)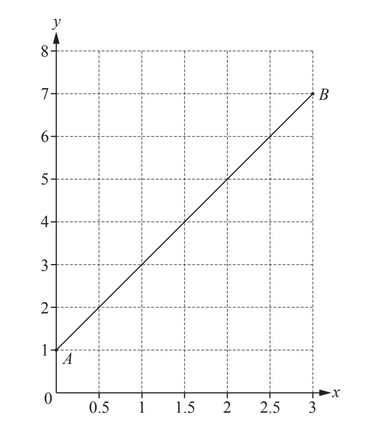
The line AB is drawn on the grid.
(i) Write down the co-ordinates of A.
(ii) Work out the gradient of the line AB.
(iii) Write down the equation of the line AB in the form y = mx + c.
y = ……………….
(b) Write down the equation of a straight line that is parallel to y = 5x – 3.
▶️Answer/Explanation
(i) The coordinates of point A are (0, 1).
(ii) To find the gradient of the line AB, we can use the formula:
Gradient \((m) =\frac{\Delta y}{\Delta x}\)
The change in y is 7 – 1 = 6, and the change in x is 3 – 0 = 3. Therefore, the gradient of the line AB is:
\(m = \frac{6}{3}= 2\)
(iii) To write down the equation of the line AB in the form y = mx + c, we need to determine the y-intercept, c.
Using the coordinates of point A (0, 1) and the gradient m = 2, we can substitute these values into the equation:
\(1 = 2\times 0 + c\)
1 = c
Therefore, the equation of the line AB is:
y = 2x + 1
(b) To find the equation of a straight line that is parallel to y = 5x – 3, we need to keep the same gradient as the given line, which is 5. Therefore, the equation of the parallel line is:
y = 5x + c, where c is the y-intercept (a constant).
Question
The diagram shows a point P and a line L.
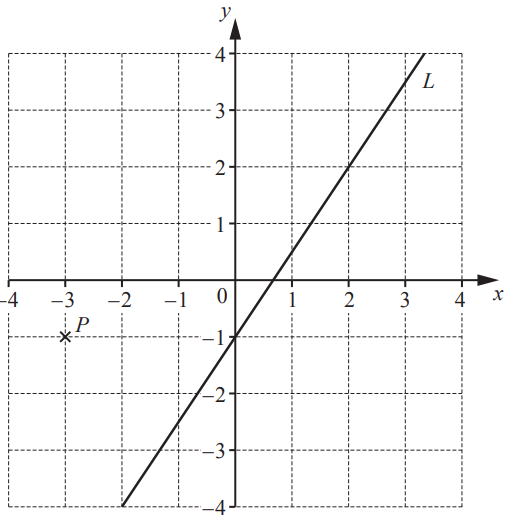
(a) Write down the co-ordinates of point P.
( ___ , ___ ) [1]
(b) Find the gradient of line L.[2]
(c) Write down the equation of line L in the form y = mx + c.
y = __ [2]
Answer/Explanation
Ans:
22(a) −3, −1
22(b) 1.5 oe
22(c) [y =] 1.5x − 1 oe
Question
(a) Write down the gradient of the line y=2x-3.
………………………………………….
(b) Complete the table of values for y=2x-3.
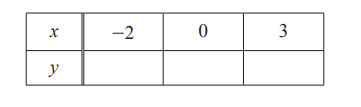
(c) On the grid, draw the graph of y=2x-3 for \(-2\leq x\leq 3.\)
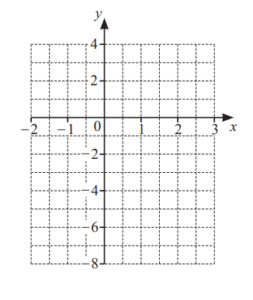
Answer/Explanation
(a) 2
(b) – 7 – 3 3
(c) Correct ruled graph
