Question
(a) (i) Complete the table of values for \(y = x^2 + x\).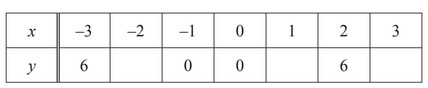
(ii) On the grid, draw the graph of \( y = x^2 + x\) for \(-3 \leq x \leq 3\).
(iii) On the grid, draw the line y = 10.
(iv) Use both your graphs to solve
\(x^2 + x = 10\) for \(-3 \leq x \leq 3\).
(b) Another line, L, has the equation \(y = \frac{2}{3}x -5\).
(i) Write down the gradient of L.
(ii) Write down the equation of a straight line that is parallel to L.
(c) 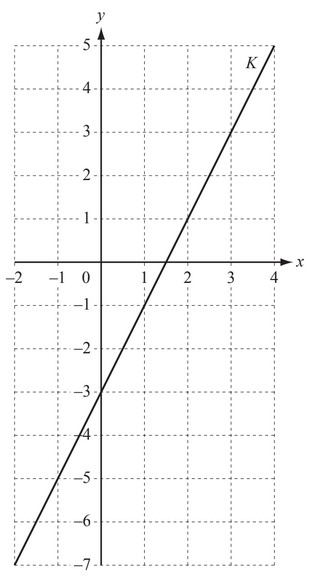
Write the equation of the line, K, in the form y = mx + c .
Answer/Explanation
Answer:
(a) (i) 2 and 2
12
(ii) 7 points correctly plotted
correct curve through the 7points
(iii) correct line
(iv) 2.6 – 2.8
(b) (i) \(\frac{2}{3}\)
(ii) \(y = \frac{2}{3}x + c\)
(c) [y=]2x – 3
Question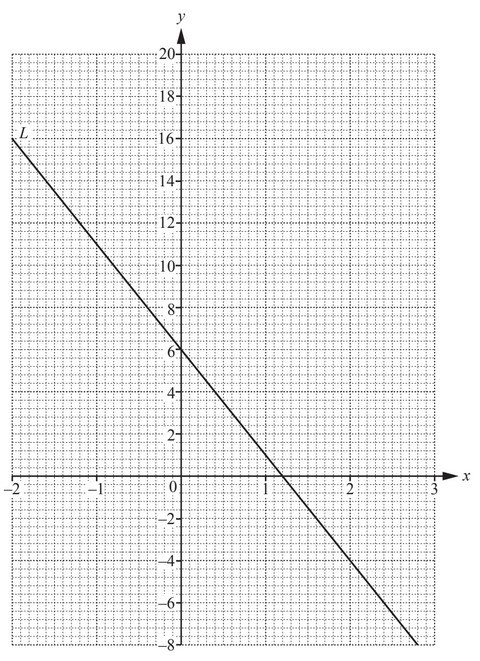
(a) The line L is drawn on the grid.
Find the equation of the line in the form y = mx + c.
y = ………………………………………..
(b) (i) Complete the table of values for \(y = x^2 + 2x + 4\).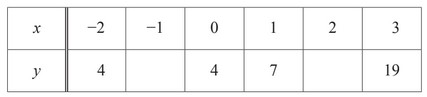
(ii) On the grid above, draw the graph of \(y = x^2 + 2x + 4\) for \(-2 \leq x \leq 3\).
(c) For \(-2 \leq x \leq 3\), write down the co-ordinate of the point of intersection of the curve \(y = x^2 + 2x + 4\)
withe the line L.
Answer/Explanation
Answer:
(a) -5x + 6
(b) (i) 3 12
(ii) Correct curve
(c) 0.2 to 0.35
Question
(a) 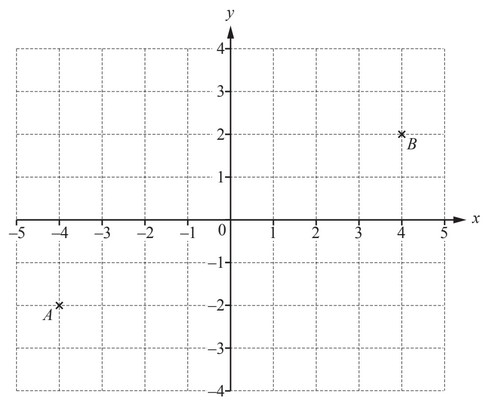
(i) Plot point C at (–4, 2).
(ii) Write down the mathematical name of the triangle formed by joining the points A, B and C.
(iii) Write down the vector \(\overheadarrow{AB}\)
\(\overheadarrow{AB} = ( )\)
(iv) (a) Find the gradient of the line AB.
(b) Write down the equation of the line AB.
y = …………………………………………
(b) (i) Complete the table of values for \(y = x^2 + x -5\).
(ii) On the grid below, draw the graph of \(y = x^2 + x – 5\) for \(-4 \leq x \leq 4\).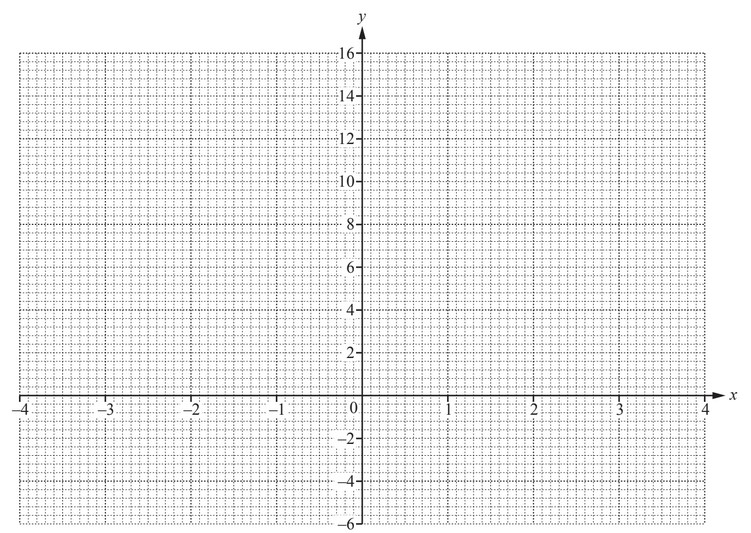
(iii) Use your graph to solve the equation \(x^2 + x – 5 = 0\)
x = ……………….. or x = ………………..
Answer/Explanation
Ans:
(a) (i) Correct point plotted
(ii) Right-angled or scalene
(iii) 8
4
(iv) (a) 0.5 oe
(iv) (b) [y =] 0.5x oe
(b) …1 …–5 –5…1 15
(ii) Correct curve
(iii) –2.8 1.8
