Question
The scale drawing shows the positions of two towns, X and Y.
The scale is 1 centimetre represents 5 kilometres.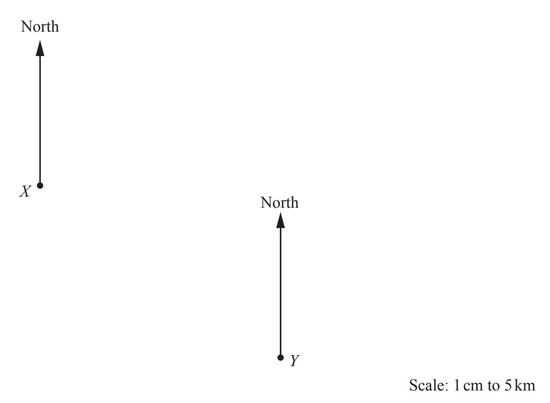
(a) Work out the actual distance from town X to town Y.
…………………………………… km
(b) Measure the bearing of town X from town Y.
(c) An airport, A, is 22.5km from town Y on a bearing of 050°.
Mark and label the position of A on the scale drawing.
Answer/Explanation
Answer:
(a) 35
(b) 305
(c) Point marked in correct position
Question
(a) A closed box, in the shape of a cuboid, has length 5cm, width 4cm and height 2cm.
(i) Draw a net of the box on the 1cm2 grid.

Answer/Explanation
Ans: Correct ruled net
(ii) A container is a cube with volume 1m3.
Work out the maximum number of these boxes that can be packed into this container.
Answer/Explanation
Ans: 25 000
(b) A shop sells three different sized boxes of rice.
The boxes all have the same cost per kilogram.

(i) Work out the cost in rupees of box B.
Answer/Explanation
Ans: 144
(ii) $1 = 64 rupees.
Calculate the mass of box C.
Give your answer in kilograms.
Answer/Explanation
Ans: 2.1
(c) Change 75cm3 into litres.
Give your answer in standard form.
Answer/Explanation
Ans: 7.5 10−2 × cao