Question
The diagram shows three triangles A, B and C on a grid.
Triangle A is shaded.
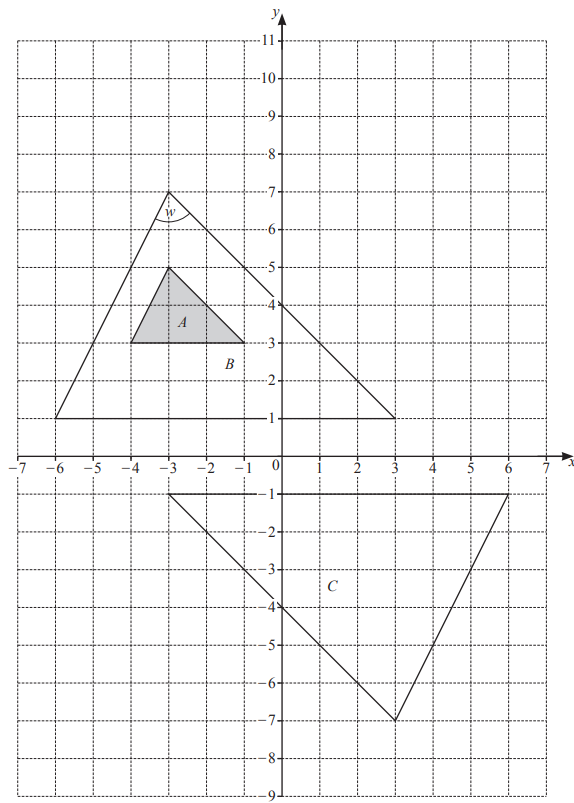
(a) Measure angle w.
Angle w = …………………………………………
(b) Explain why triangle B is congruent to triangle C.
…………………………………………………………………………………………………………………………………..
(c) Describe fully the single transformation that maps
(i) triangle A onto triangle B,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(ii) triangle B onto triangle C.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(d) On the grid, draw the image of
(i) shape A after a translation by the vector \(\begin{pmatrix}7\\ -1\end{pmatrix}\)
(ii) shape A after a reflection in the line y =-1.
Answer/Explanation
(a) 72
(b) Correct reason
(c)(i) Enlargement
[centre] ( − 3, 4)
[scale factor] 3
(ii)Rotation
[centre] (0,0) oe
180° oe
(d)(i) Correct translation
(3,2),(4,4),(6,2)
(ii) Correct reflection
( −1,-5), ( −3,- 7 ), (−4,–5)
Question
(a) On each of the following shapes draw any lines of symmetry.
(i) 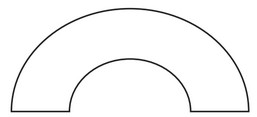
(ii) 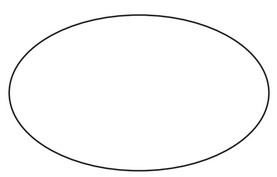
(b) Complete this shape by shading one square so that it has rotational symmetry of order 2.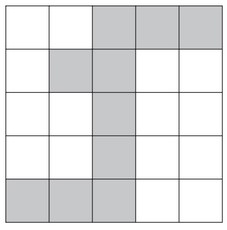
(c) 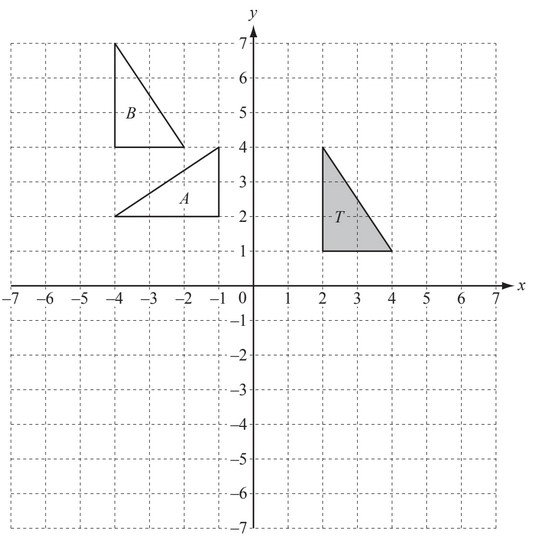
On the grid, draw the image of triangle T after a
(i) refl ection in the line x = 4,
(ii) translation by the vector \(\binom{-5}{-4}\)
(iii) rotation, centre (4, 1) through 180°.
(d) Describe fully the single transformation that maps
(i) triangle T onto triangle A,
(ii) triangle T onto triangle B.
Answer/Explanation
Answer:
(a) (i) one correct line
(ii) only two correct lines
(b) correct square
(c) (i) correct reflection
(ii) correct translation
(iii) correct rotation
(d) (i) rotation
centre (0,0)
angle 90°
[anticlockwise]
(ii) translation
\(\binom{-6}{3}\)
Question
(a) Complete the table of values for \(y = x^2 + 2x – 1\).
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 14 | 2 | -1 | -1 | 2 |
(b) On the grid, draw the graph of \(y = x^2 + 2x – 1\). for \(-5 \leq x \leq 3\).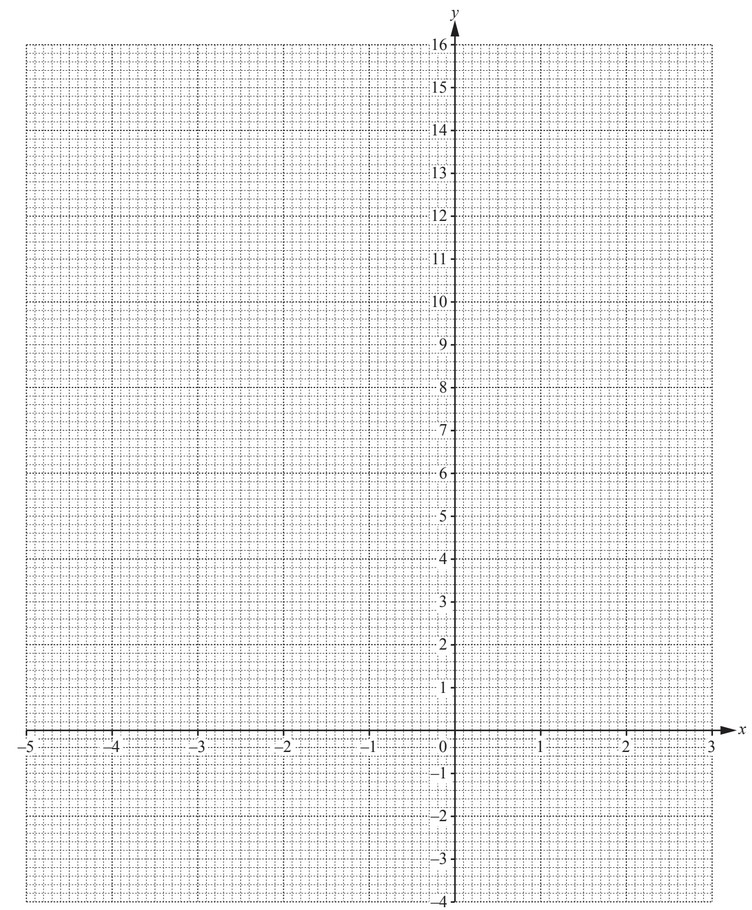
(c) (i) On the grid, draw the line of symmetry.
(ii) Write down the equation of the line of symmetry.
(d) (i) On the grid, plot the points (-5, 7) and (0, -3) and join them with a straight line, L.
(ii) Write down the x co-ordinate of each point where the line L crosses the graph of \(y = x^2 + 2x -1\).
x = …………………… and x = ……………………
(iii) Work out the gradient of the line L.
Answer/Explanation
Answer:
(a) 7 -2 7 14
(b) Correct smooth curve
(c) (i) Ruled line, x = –1, drawn
(ii) x = –1 oe
(d) (i) Ruled line L drawn, joining
(–5, 7) and (0, −3)
(ii) −3.3 to −3.5, −0.5 to −0.7
(iii) −2
