Question
(a) One day, Mahika records the number of teachers and students who cycle to school.
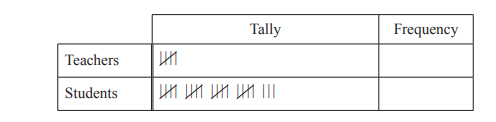
(i) Complete the frequency column in the table.
Answer/Explanation
Ans: 5 23
(ii) Work out the percentage of people who cycle that are students.
Answer/Explanation
Ans: 82.1 or 82.14…
(b) Mahika records how 120 students from Year 1 and Year 2 travel to school.
Each student walks, cycles or travels by bus.
• 48 students are in Year 1.
• 77 students walk.
• 5 students in Year 2 cycle.
• 36 students travel by bus.
• \(\frac{4}{9}\) of the students who travel by bus are in Year 1.
(i) Complete the table.
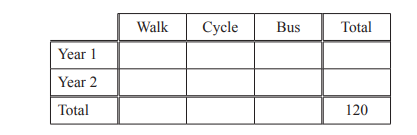
Answer/Explanation
Ans: 30 2 16 48
47 5 20 72
77 7 36 [120]
(ii) One of the 120 students is chosen at random.
Work out the probability that this student does not travel by bus to school.
Answer/Explanation
Ans: \(\frac{7}{10}oe\)
(c) There have been 24 complaints about one of the buses.
The complaints are:
• The bus is late.
• The price is too high.
• The bus is crowded.
(i) Complete the table.
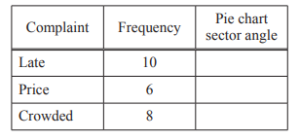
Answer/Explanation
Ans: 150, 90, 120
(ii) Complete the pie chart.
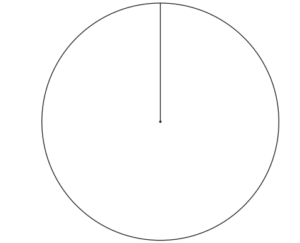
Answer/Explanation
Ans: Correct pie chart drawn
Question
(a) Write twenty five million in figures.
(b) Write the following in order of size, starting with the smallest.
\(\frac{2}{3}\) 65% 0.6
(c) In a sale a coat costing \(\$250\) is reduced to \(\$200\)
Find the percentage decrease in the cost.
(d)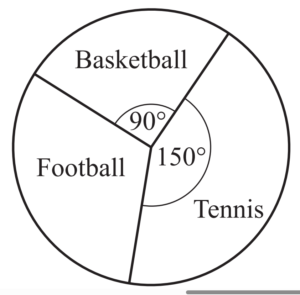
120 students are asked to choose their favourite sport.
The results are shown in the pie chart.
Calculate the number of students who chose
(i) basketball,
(ii) football
Answer/Explanation
(a) Twenty-five million written in figures is 25,000,000
(b) To compare them, we convert the fractions and percentages to decimal form:
0.6 = 0.60
\(\frac{2}{3}\) = 0.666…
65% = 0.65
Therefore, 0.6<6.5%<\(\frac{2}{3}\)
(c) The difference between the original price and the sale price is:
\(\$250\) – \(\$200\) = \(\$50\)
Now,
Percentage decrease = (\frac{difference}{original price} \times 100%\)
Plugging in the values we get:
Percentage decrease = \(\frac{\$50}{\$250} \times 100%\)
= \(0.2\times 100%\)
= 20%
Therefore, the percentage decrease in the cost of the coat is 20%.
(d) (i) 30
(ii) 40
