Question

The table shows the average temperature for Tromso, Norway each month.
(a) (i) Write down the month which had the highest average temperature.
(ii) How much warmer was it in September than in February?
(iii) The lowest temperature in October was 12.3°C below the average temperature for that
month.
Work out the lowest temperature in October.
(b) In a survey, some tourists were asked how they had travelled to Norway.
The pie chart shows the results.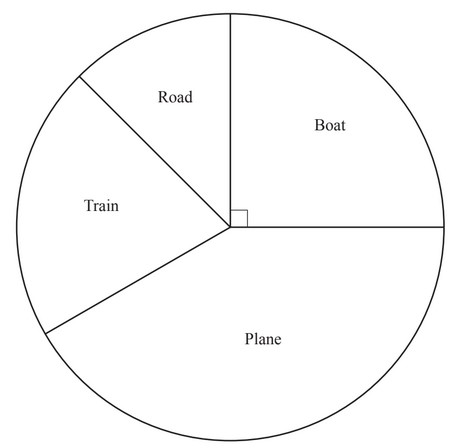
(i) 150 of these tourists travelled by boat.
Show that 600 tourists took part in the survey.
(ii) Calculate the number of these tourists who travelled by plane.
(c) A train ticket from Oslo to Stavanger costs 885 krone.
There is a discount of 12% on the total cost of the tickets for a group of 10 or more people.
Calculate the cost of tickets for a group of 15 people.
(d) On 1 January 2000, the population of Norway was 4480 000, correct to 3 signifi cant fi gures.
(i) Write this number in standard form.
(ii) On 1 January 2011, the population of Norway was 4920000, correct to 3 signifi cant fi gures.
Calculate the percentage increase in the population.
Answer/Explanation
Answer:
(a) (i) July or Jul
(ii) 10.9
(iii) -9.6
(b) (i) \(150 \div \frac{90}{360}\) oe
(ii) 250
(c) 11682
(d) (i) \(4.48 \times 10^6\) cao
(ii) 9.82
Question
Pedro is on a cruise ship.
(a) The ship has a climbing wall.
These are the number of attempts that each of 30 people made at climbing the wall.
29 27 11 3 12 4 29 9 16 17 30 29 38 36 18
2 15 24 36 3 33 26 21 9 38 4 28 23 19 27
(i) Find the range.
(ii) Complete the frequency table.
You may use the tally column to help you.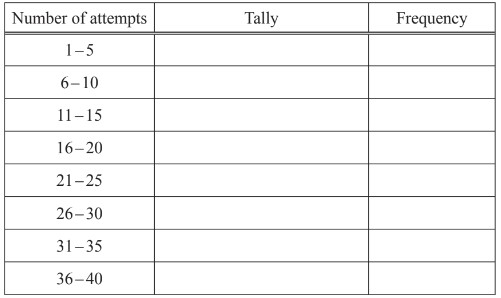
(iii) Draw a bar chart to show this information.
Complete the scale on the frequency axis.
(iv) Write down the modal group.
(b) Pedro left the ship in Cadiz at 0845.
He returned to the ship at 1610.
Find how long Pedro was in Cadiz.
(c) Exchange Rate
$1 = €1.428
(i) Pedro changed $167 into euros (€).
Calculate how many euros Pedro received.
Give your answer correct to 2 decimal places.
(ii) Later, Pedro changed €107.10 back into dollars ($) using the same exchange rate.
Calculate how many dollars Pedro received.
Answer/Explanation
Answer:
(a) (i) 36 cao
(ii) 5, 2, 3, 4, 3, 8, 1, 4
(iii) fully correct bar chart
(iv) 26 – 30 cao
(b) 7 (hours) 25 ( minutes) cao
(c) (i) 238.48
(ii) 75
Question
The table shows the height, in metres, above sea-level and the temperature, in °C, at midday for some
places on a mountain.
(a) Complete the scatter diagram for these results.
The fi rst four points have been plotted for you.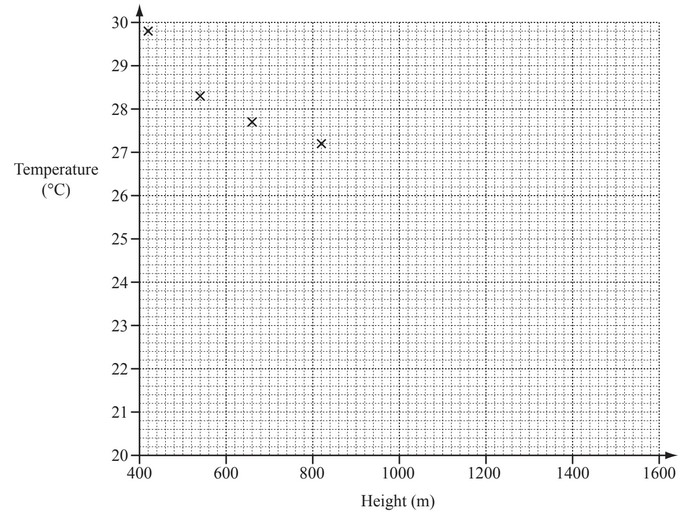
(b) What type of correlation does this scatter diagram show?
(c) On the grid, draw the line of best fit.
(d) Use your line of best fit to estimate the temperature at a height of 1400m.
Answer/Explanation
Answer:
(a) 4 points plotted correctly
(b) negative
(c) correct ruled line
(d) 22.4 – 22.8
Question
The table shows a summary of the types of employment for 90 people.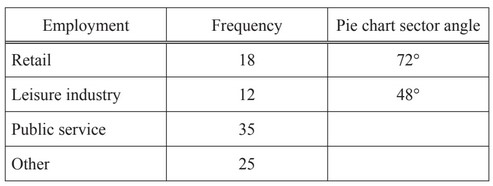
(a) (i) Complete the table.
(ii) Complete the pie chart and label the sectors.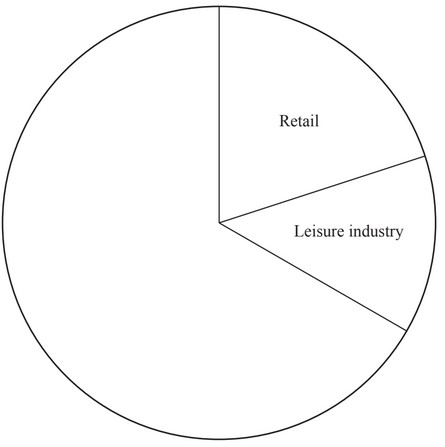
(b) Here are the ages of the people working in the leisure industry.
16 17 19 23 23 24 27 31 33 40 45 56
(i) Work out the range.
(ii) Calculate the mean.
(iii) Sabrina wants to interview someone working in the leisure industry.
She chooses one person at random.
Write down the probability that the person chosen is under 30 years old.
Answer/Explanation
Answer:
(a) (i) 140
(ii) 100
(ii) correct labelled pie chart
(b) (i) 40
(ii) 29.5
(iii) \(\frac{7}{12}\) oe
Question
(a) One day a survey is taken of the ages of 120 children at a fairground.
The results are shown in the frequency table.
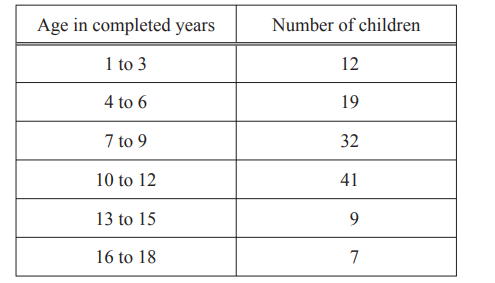
(i) On the grid, draw a bar chart for this data.
Complete the scale on the frequency axis.
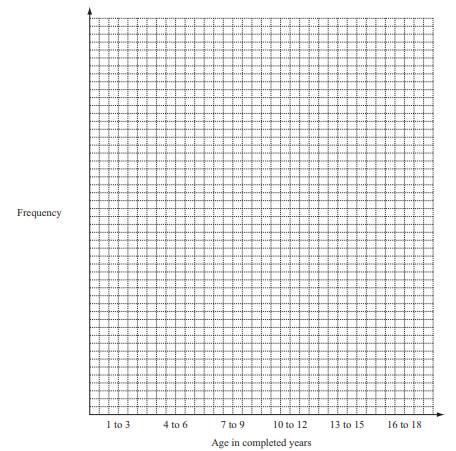
Answer/Explanation
Ans: Correct diagram with scale
(ii) What is the modal age group?
Answer/Explanation
Ans: 10 to 12 cao
(iii) One of the 120 children is chosen at random.
Write down the probability that the child is aged 4 to 6.
Answer/Explanation
Ans: \(\frac{19}{120}\) or 0.158[3….] or 15.8[3……]%
(b) Lalia says the probability of taking a yellow bead from a bag containing yellow beads and black beads is \(\frac{7}{5}.\)
Explain why \(\frac{7}{5}\) cannot be a correct probability
Answer/Explanation
Ans: Probability must be between 0 and 1 oe
(c) Another bag contains 9 green marbles and 11 red marbles.
A marble is taken at random.
Write down the probability that the marble is
(i) green,
Answer/Explanation
Ans: \(\frac{9}{20}\) or 0.45 or 45%
(ii) blue.
Answer/Explanation
Ans: 0 oe
Question
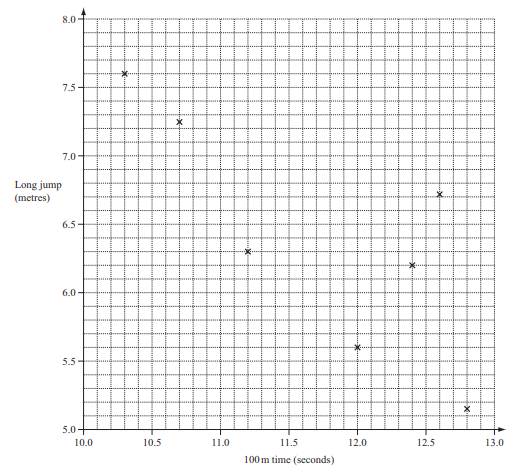
12 athletes took part in the 100 metres race.
11 of these athletes also took part in the long jump.
The times and distances, each measured correct to 3 signifi cant fi gures, for these athletes are shown in the
table.

(a) The scatter diagram shows the times and distances for athletes B to H.
(i) Plot the times and distances for athletes I, J, K and L.
Answer/Explanation
Ans:
(ii) On the scatter diagram, draw a line of best fi t.
Answer/Explanation
Ans:
(iii) Athlete A did not take part in the long jump.
Use your line of best fi t to estimate a long jump distance for athlete A.
Answer/Explanation
Ans:
(iv) What type of correlation is shown on the scatter diagram?
Answer/Explanation
Ans:
(v) Describe in words the relationship between the time for 100 metres and the distance in the long jump.
Answer/Explanation
Ans:
(b) Use the table of times and distances to work out
(i) the mean of the 100 metres times,
Answer/Explanation
Ans:
(ii) the percentage of athletes who ran 100 metres in less than 11.5 seconds,
Answer/Explanation
Ans:
(iii) the range of the distances jumped by the 11 athletes, B to L.
Answer/Explanation
Ans:
Question
(a) Luis buys a season ticket to watch his local football team.
The season ticket costs $595.
(i) Luis buys the season ticket online and gets a 5% discount on the $595.
Work out how much Luis pays for the season ticket online.
Answer/Explanation
Ans: 565.25
(ii) A ticket to watch one match costs $38.
Luis watches 16 matches.
How much did Luis save by buying a season ticket online instead of 16 tickets at $38 each?
Answer/Explanation
Ans: 42.75
(b) The football stadium has 26272 seats.
The number of people who attend one match is 23854.
Calculate the percentage of the 26272 seats that are empty.
Answer/Explanation
Ans: 9.2[0…]
(c) The total number of people attending matches at the stadium last season was 506762.
Write 506762 in standard form, correct to 3 significant figures.
Answer/Explanation
Ans: 5.07 × 105 cao
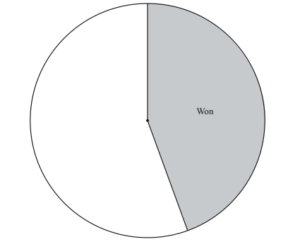
(d) Last season the team played a total of 45 matches.
The table shows the results of these matches.
| Result | Number of matches | Pie chart sector angle |
| Won | 20 | 160° |
| Drawn | 15 | |
| Lost | 10 |
(i) Complete the table.
Answer/Explanation
Ans: 120°
80°
(ii) Complete the pie chart.
Answer/Explanation
Ans: Pie chart correct
(e) The table shows the total attendance figures for all the teams in the league for two seasons.
| Season | Total attendance |
| A | 9.76 × 106 |
| B | 1.36 × 107 |
Work out how much greater the attendance was in season B than in season A.
Give your answer in standard form.
Answer/Explanation
Ans: 3.84 × 106
Question
All the children in a school are asked to choose their favourite colour.
The pie chart shows the results.
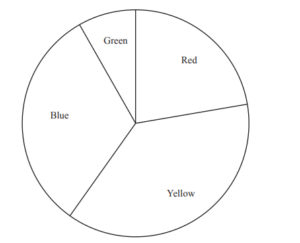
(a) Write down the least favourite colour chosen.
Answer/Explanation
Ans: green
(b) 27 children choose yellow as their favourite colour.
Work out the total number of children in the school.
Answer/Explanation
Ans: 72
(c) Work out the percentage of the children in the school who choose red.
Answer/Explanation
Ans: 22.2
Question
(a) Ten students take a physics examination and a mathematics examination.
Their scores are recorded in the table below.
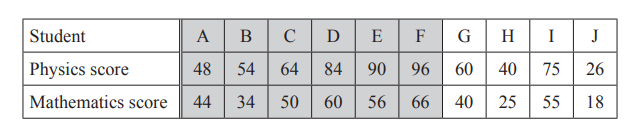
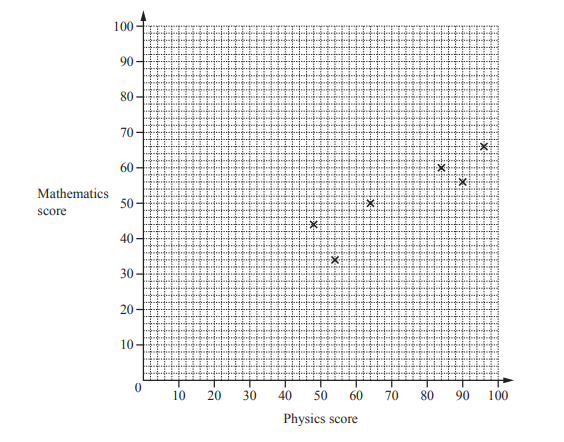
(i) Complete the scatter diagram.
The first six points have been plotted for you.
Answer/Explanation
Ans: 4 points correctly plotted
(ii) What type of correlation is shown by the scatter diagram?
Answer/Explanation
Ans: positive
(iii) On the grid, draw a line of best fit.
Answer/Explanation
Ans: correct ruled straight line
(iv) Another student scored 52 in the mathematics examination.
Use your line of best fit to estimate this student’s score in the physics examination.
Answer/Explanation
Ans: 74
(b) This graph can be used to convert between pounds (lb) and kilograms (kg).
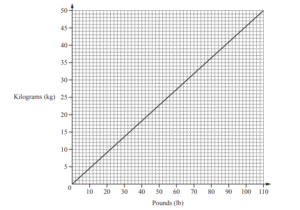
Use the graph to convert
(i) 50 pounds to kilograms,
Answer/Explanation
Ans: 22 < Ans ≤ 23
(ii) 275 kilograms to pounds.
Answer/Explanation
Ans: 590 ≤ ans ≤ 620
Question
(a) Parminder sells dresses.
The pie charts show information about the colour of dresses she sold.
She sold 250 dresses in 2013 and 280 dresses in 2014.
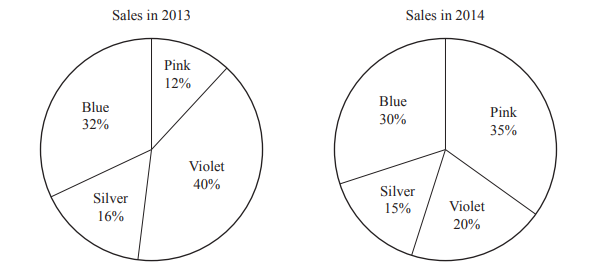
(i) Write down the most popular colour of dress she sold in 2013.
Answer/Explanation
Ans:Violet
(ii) Write down the fraction of dresses sold in 2014 that were either pink or silver.
Answer/Explanation
Ans: \(\frac{50}{100}oe\)
(iii) Write down the ratio of Blue :Pink dresses sold in 2013.
Give your answer in its simplest form.
Answer/Explanation
Ans: 8:3
(iv) Work out how many more pink dresses were sold in 2014 than in 2013.
Answer/Explanation
Ans: 68
(v) Complete the table by writing True or False beside each statement.
The first answer has been completed for you.
| Statement | True or False |
| 40% of the dresses sold in 2013 were violet. | True |
| Blue was the second most popular colour in both 2013 and 2014. | |
| One third of the dresses sold in 2014 were blue. | |
| Violet was more popular than silver in both 2013 and 2014 |
Answer/Explanation
Ans:
| Statement | True or False |
| 40% of the dresses sold in 2013 were violet. | True |
| Blue was the second most popular colour in both 2013 and 2014. | True |
| One third of the dresses sold in 2014 were blue. | False |
| Violet was more popular than silver in both 2013 and 2014 | True |
(vi) From 2013 to 2014 the number of silver dresses sold has increased but the percentage sold has decreased.
Give a reason why the percentage sold has decreased.
You do not need to do any calculations.
Answer/Explanation
Ans: [The] percentage is [smaller but it is] of a larger [total] number [of dresses]
(b) The table shows the number of metres of silk needed to make a dress.
Dress length | Height of customer to the nearest 10cm | |||
| 160 cm | 170 cm | 180cm | 190cm | |
| Short | 4.0 | 4.3 | 4.6 | 4.9 |
| Medium | 4.8 | 5.0 | 5.2 | 5.4 |
| Long | 5.5 | 5.8 | 6.2 | 6.6 |
Silk costs $12.50 per metre.
It takes 6 hours to make one dress.
The dressmaker charges $9.25 per hour.
A customer orders a dress for each of her two daughters.
She orders a long dress for one daughter who is 160cm tall.
She orders a short dress for her other daughter who is 176cm tall.
Calculate the total cost of the two dresses.
Answer/Explanation
Ans: 237.25
Question
(a) Juan and his family fly from London to Rio de Janeiro.
(i) The plane departs at 10 20 and arrives in Rio de Janeiro 11 hours 40 minutes later.
The local time in Rio de Janeiro is 5 hours behind the local time in London.
Work out the time in Rio de Janeiro when the plane arrives.
(ii) The total cost of the plane tickets is 3500 pounds (£).
The exchange rate is £1 = 4.45 Brazilian Real.
Calculate the cost of the tickets in Brazilian Real.
………………………………… Real
(b) (i) Juan and his family go to a soccer match.
He buys 2 adult tickets and 2 child tickets.
The price of an adult ticket is 660 Brazilian Real.
The price of a child ticket is \(\frac{2}{3}\) of the price of an adult ticket.
Calculate the total cost of the tickets.
………………………………… Real
(ii) The length, x metres, of the soccer pitch is 105m, correct to the nearest metre.
Complete the statement about the value of x.
……………………………… \(\leq \) x < ………………………………
(c) The table shows how Juan and his family spent their time in Rio de Janeiro.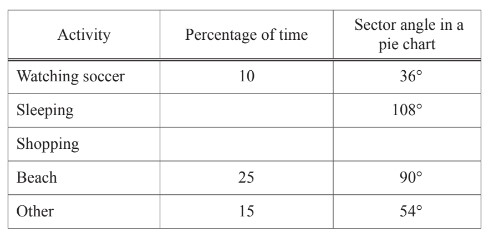
(i) Complete the table.
(ii) Complete the pie chart.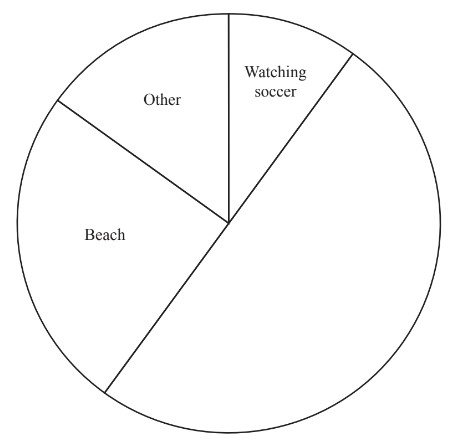
Answer/Explanation
Answer:
(a) (i) 1700 or 5pm
(ii) 15 575
(b) (i) 2200
(ii) 104.5
105.5
(c) (i) 30
20 72
(ii) Correct pie chart
Question
Joel spins a fair five-sided spinner numbered 2, 3, 4, 5 and 6.
(a) Write down the probability that the spinner lands on
(i) an odd number,
(ii) a prime number,
(iii) the number 7.
(b) Here are the results of his first 20 spins.
| Number | 2 | 3 | 4 | 5 | 6 |
| Frequency | 3 | 2 | 6 | 4 | 5 |
(i) Write down the mode.
(ii) Calculate the mean.
(iii) Joel wants to draw a pie chart to show the results in the table.
(a) Show that the sector angle for the number 2 is 54°.
(b) Find the sector angle for the number 6.
(c) Joel asks 30 students to guess the number that the spinner will next land on.
The results are shown in this pie chart.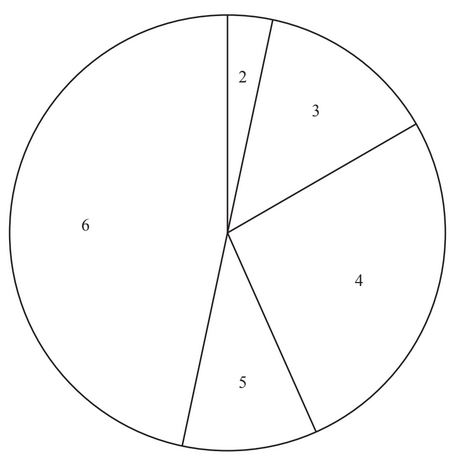
(i) The sector angle for the number 6 is 168°.
How many students guessed the number 6?
(ii) Find the percentage of the students who guessed a number less than 5.
……………………… %
(iii) Joel spins the spinner.
10% of the 30 students guessed correctly.
Which number did the spinner land on?
Answer/Explanation
Answer:
(a) (i) \(\frac{2}{5}\) oe
(ii) \(\frac{3}{5}\)oe
(iii) 0
(b) (i) 4
(ii) 4.3
(iii) (a) \(\frac{3}{20} \times 360\)
(iii) (b) 90
(c) (i) 14
(ii) 43.3
(iii) 5
Question
Ten students each take two French tests.
Their marks are recorded in the table below.
(a) One of the ten students is chosen at random.
Find the probability that their mark on Test 2 is higher than their mark on Test 1.
(b) (i) Complete the scatter diagram.
The first six points have been plotted for you.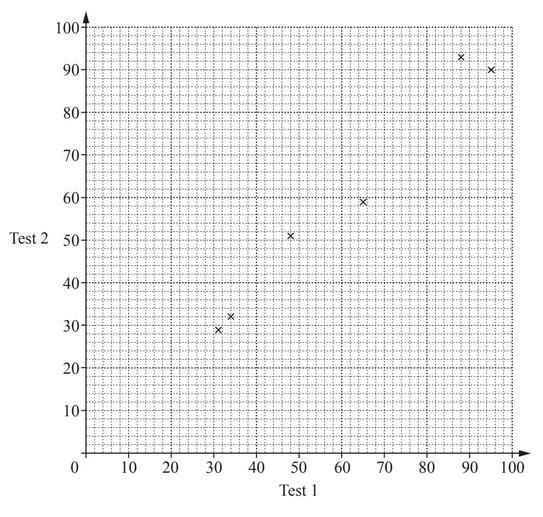
(ii) What type of correlation is shown on the scatter diagram?
(iii) On the grid, draw the line of best fit.
(iv) Another student scored 45 marks on Test 2.
Use your line of best fit to estimate the mark for this student on Test 1.
(v) A different student scored 10 marks on Test 1.
Explain why you should not use your scatter diagram to estimate their mark on Test 2.
Answer/Explanation
Ans:
(a) \(\frac{2}{10}\) oe
(b) (i) 4 points correctly plotted
(ii) positive
(iii) correct ruled line
(iv) 46 to 48
(v) 10 is not in range of recorded
test 1 results
Question
Here is a sequence of diagrams made using identical rectangles.
A dot is shown at the junction of three lines.
A cross is shown at the junction of two lines.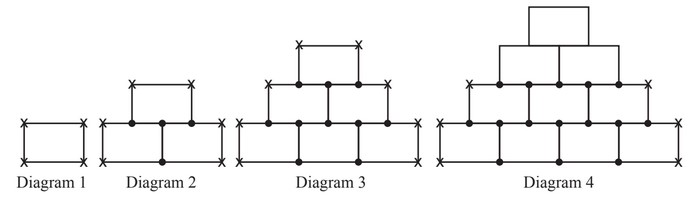
(a) Write down the order of rotational symmetry of Diagram 1.
(b) Complete Diagram 4 using dots and crosses.
(c) Complete the table for Diagram 4 and Diagram 5.
| Diagram | 1 | 2 | 3 | 4 | 5 |
| Number of dots | 0 | 4 | 10 | ||
| Number of crosses | 4 | 6 | 8 |
(d) (i) Describe, in words, the rule for continuing the sequence for the number of dots.
(ii) The expression for the number of dots in Diagram n is \(n^2 + n – 2\).
Find the number of dots in Diagram 12.
(e) (i) Write down an expression for the number of crosses in Diagram n.
(ii) Diagram n has 100 crosses.
Find the value of n.
n = …………………………………………
Answer/Explanation
Answer:
(a) 2
(b) 3 dots correctly placed
4 crosses correctly placed
(c) 18 28
10 12
(d) (i) Add two more each time oe
(ii) 154
(e)(i) 2n + 2 oe final answer
(ii) 49
Question
Francis asks 30 families how many children they have.
The table shows the results.
| Number of children in each family | 0 | 1 | 2 | 3 | 4 | 5 |
| Number of families | 4 | 6 | 6 | 2 | 9 | 3 |
(a) (i) Write down the mode.
(ii) Find the median.
(iii) Calculate the mean.
(iv) Complete the bar chart, including the vertical scale.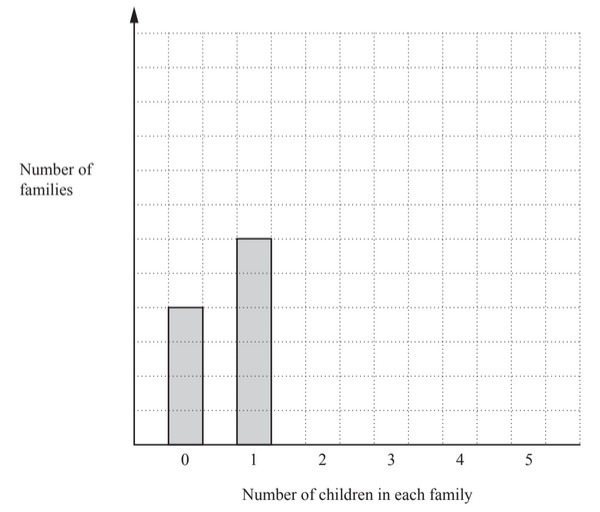
(b) Francis also recorded the age group and gender of the children aged 12 or less.
The information is shown in the table.
| Age 4 and younge | Age 5 to 8 | Age 9 to 12 | Total | |
| Male | 9 | 36 | ||
| Female | 11 | |||
| Total | 30 | 20 | 75 |
Complete the table.
(c) Francis displays the results for the totals of each age group on a pie chart.
The sector angle for the group ‘Age 4 and younger’ is 120°.
Calculate the sector angle for
(i) age 5 to 8,
(ii) age 9 to 12.
(d) Complete the pie chart.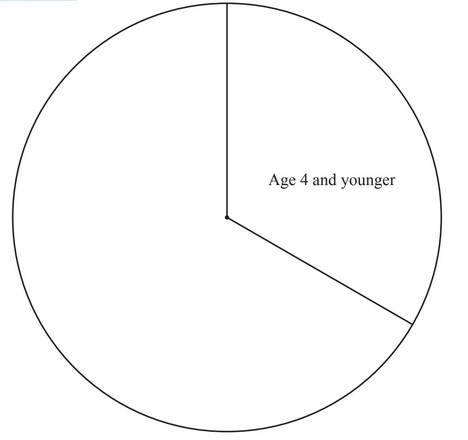
Answer/Explanation
Answer:
(a) (i) 4
(ii) 2
(iii) 2.5
(iv) 4 bars correct height, correct
width and correct gaps
Correct vertical scale shown
(b) 6 values correctly placed
14 16 [9] 39
[11] 14 11 [36]
25 [30] [20] [75]
(c) (i) 144
(ii) 144
(d) Correct line from centre to
circumference, angles 144° and
96°
Question
Ten students estimate the length and width of their rectangular school hall.
The results are shown in the table.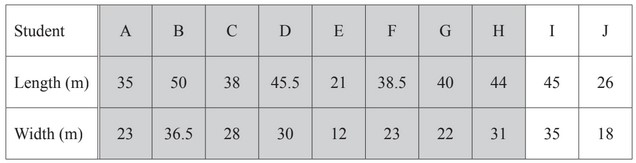
The first 8 results have been plotted on the scatter diagram.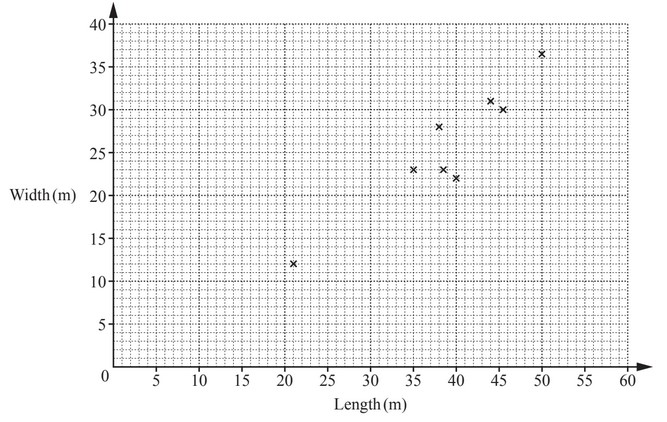
(a) On the scatter diagram, plot the results for students I and J.
(b) What type of correlation is shown by this scatter diagram?
(c) (i) On the scatter diagram, draw a line of best fit.
(ii) Another student, Pedro, estimates the length of the hall as 31m.
His result for the width is missing.
Use your line of best fit to estimate his result for the width.
……………………….. m
(d) The actual measurements of the hall are length 44m and width 34m.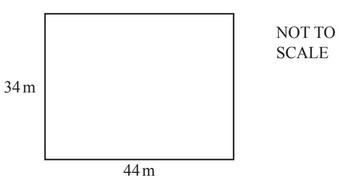
(i) The teacher says a ‘good estimator’ has both estimates no more than 5m from the actual
measurements.
Write down the letters of the students who are ‘good estimators’.
(ii) Work out the perimeter of the hall.
…………………… m
(iii) Calculate the length of a diagonal of the hall.
…………………………… m
(e) The hall is divided into two areas.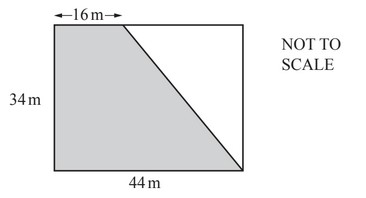
Find the shaded area.
………………………. \(m^2\)
Answer/Explanation
Answer:
(a) I, J correctly plotted
(b) positive
(c) (i) ruled line of best fit
(ii) 16 to 19
(d) (i) D,H, I
(ii) 156
(iii) 55.6 or 55.60 to 55.61
(e) 1020
Question
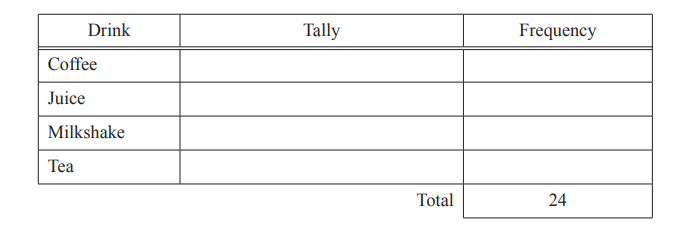
Lena owns a café.
(a) One day, Lena records the drinks she sells in one hour.

(i) Complete the frequency table.
You may use the tally column to help you.
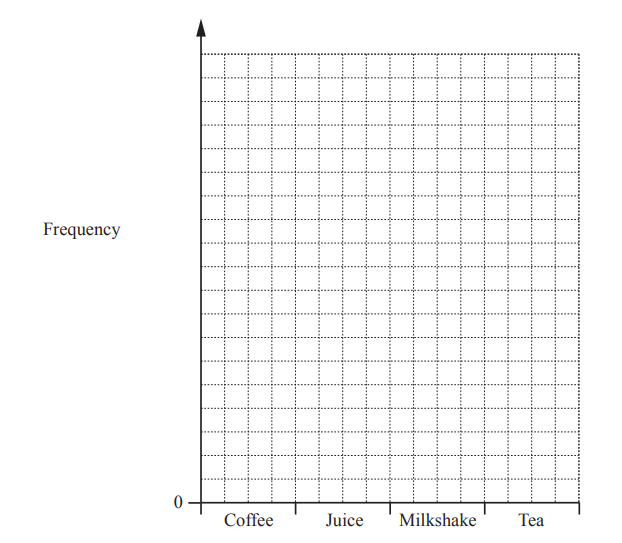
(ii) Draw a bar chart to show this information.
Complete the scale on the frequency axis.
(b) This table shows the opening hours of the café.
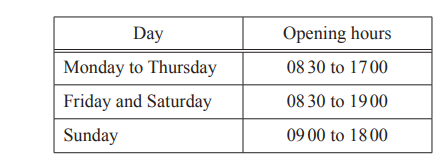
(i) Work out the total number of hours the café is open in one week.
………………………………… hours
(ii) Lena is in the café for 40 hours each week.
Ron is in the café when Lena is not there.
Calculate the percentage of the total opening hours that Ron is in the café each week.
………………………………………%
(c) Saddak buys 3 cups of tea and 2 cookies for \($6.95 .\)
A cup of tea costs \($1.75 .\)
Work out the cost of one cookie.
\($ …………………………………………\)
(d) The price of a cake is \($2.60 .\)
At the end of the day, Lena reduces the price of each cake by 35%.
Calculate the reduced price of a cake.
\($ …………………………………………\)
Answer/Explanation
(a)(i) 7, 3, 6, 8
(ii) Correct bar chart with scaled
frequency axis
(b)(i) 64
(ii) 37.5
(c) [0].85
(d) 1.69
Question
Question
Lucy asked 12 people how many hours they each spent playing a computer game and the number of levels
they each completed in one month.
The results are shown in the table.

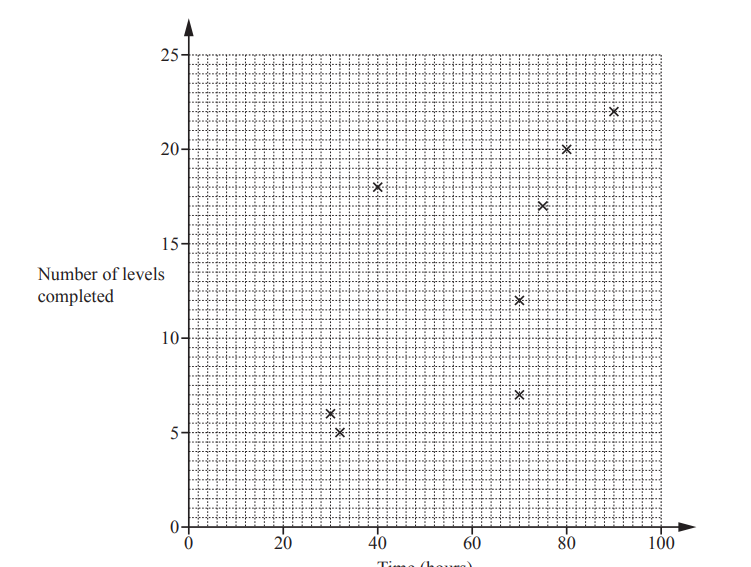
(a) Complete the scatter diagram.
The first eight points have been plotted for you.
(b) One person completes more levels per hour than any of the others.
On the scatter diagram, put a ring around the point for this person.
(c) What type of correlation does this scatter diagram show?
…………………………………………
(d) On the scatter diagram, draw a line of best fit.
(e) Another person, Monika, completed 19 levels but forgot to record the time spent playing.
Use your line of best fit to estimate the number of hours that Monika spent playing.
………………………………… hours
Answer/Explanation
(a) 4 points correctly plotted
(b) (40, 18) indicated
(c) Positive
(d) Correct ruled line
(e) 76 to 80
Question
Mr Marr asks his mathematics class to complete a statistics project about books.
(a) Olga counts the number of letters in each of the last 50 words in the book she is reading.
She has only counted the letters in 43 words so far.
Her results for these 43 words are shown in the table below.
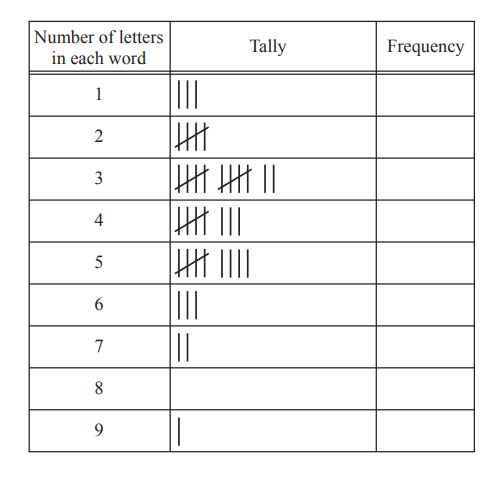
The last seven words in the book that Olga needs to add to the table are
………. and they all lived happily ever after.
(i) Complete the tally and frequency columns in the table.
(ii) Find the range.
…………………………………………
(iii) Find the median.
…………………………………………
(b) Billie asks 60 students in his school what their favourite type of book is.
He has started to draw a pictogram to show his results.
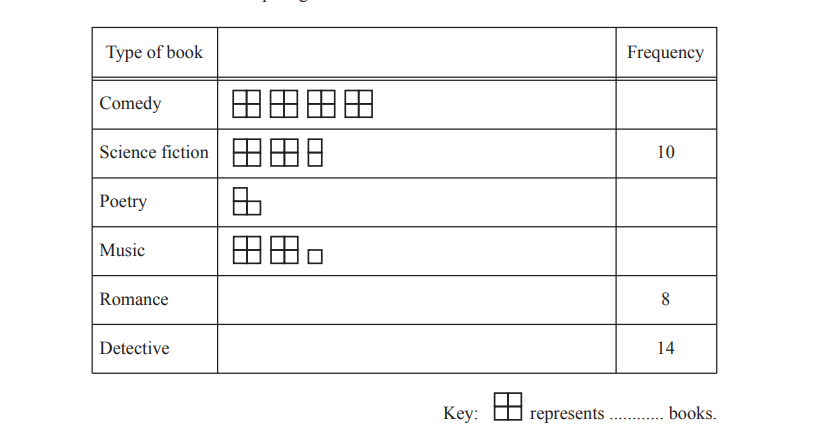
The science fiction row in the pictogram is complete.
(i) Complete the key.
(ii) Complete the pictogram.
(iii) Write down the mode.
…………………………………………
(iv) Work out how many more students choose detective books than music books.
…………………………………………
(v) Work out the fraction of students who did not choose romance books.
………………………………………….
Answer/Explanation
(a)(i) Tally for 3, 4, 5 increased by two.
Tally for 7 increased by one.
Frequencies
3, 5, 14, 10, 11, 3, 3, 0, 1
(ii) 8
(iii) 4
(b)(i) 4
(ii) 2 and 3.5 boxes drawn
16, 3 and 9 frequencies
(iii) Comedy
(iv) 5
(v)\(\frac{52}{60}\)
Question
(a) Some people go fishing and catch four types of fish.
Some information is shown in the table
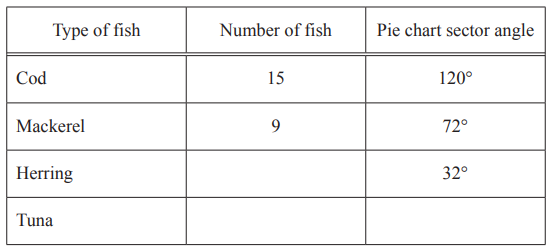
(i) Complete the table.
(ii) Complete the pie chart.
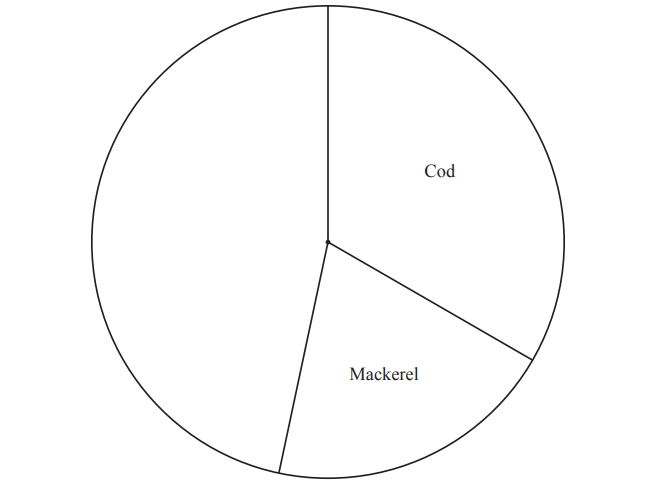
(b) Records show that \(\frac{14}{3}\) of all mullet caught are underweight.
In one day, 168 mullet are caught.
Work out the expected number of mullet that are underweight.
Answer/Explanation
(a)(i)4
17 36
(ii)\(32^{\circ} \) sector drawn
(b) 36
Question
The line L is shown on the grid.
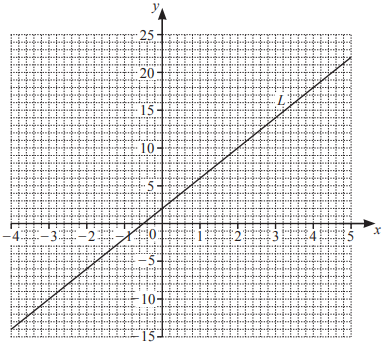
(a) Find the equation of the line L in the form y = mx + c.
y = [3]
(b) The equation of a different line is y = 3x – 4.
(i) Write down the gradient of this line.[1]
(ii) Write down the co-ordinates of the point where this line crosses the y˗axis.
( ___ , ___ ) [1]
(c) On the grid, draw the graph of y = – 2x+1 for \(-4\leqslant x\leqslant 5\).[3]
Answer/Explanation
Ans:
6(a) 4x + 2
6(b)(i) 3
6(b)(ii) (0, –4)
6(c) Correct ruled line
from x = –4 to x = 5
Question
Fourteen students each take two tests in French, a speaking test and a written test.
The table shows the scores.

(a) Complete the scatter diagram.
The first ten points have been plotted for you.[2]
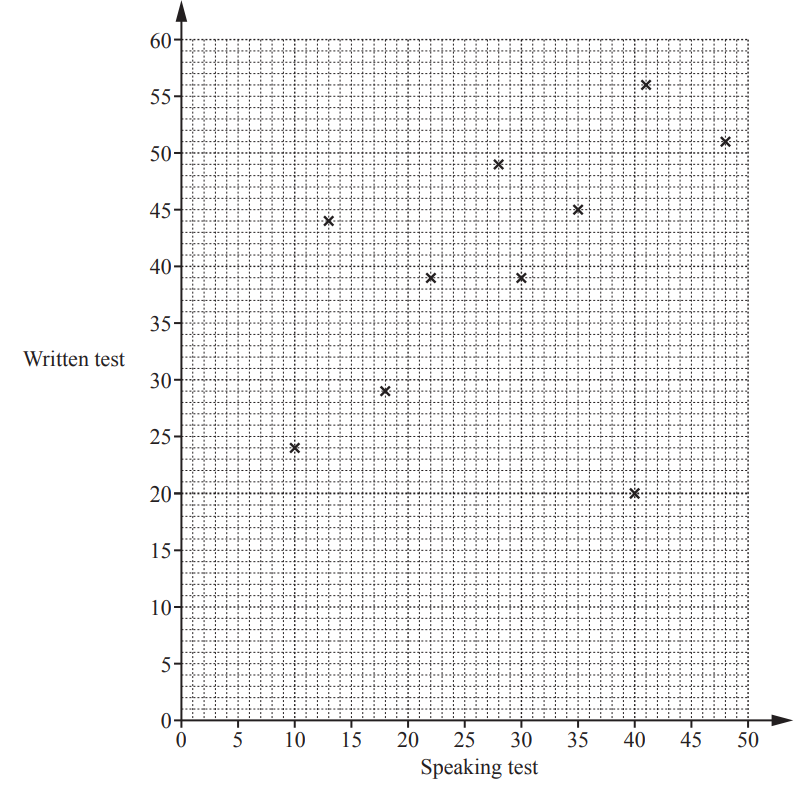
(b) What type of correlation is shown in this scatter diagram?[1]
(c) One student has a high score in the speaking test and a low score in the written test.
On the scatter diagram, put a ring around this point. [1]
(d) On the scatter diagram, draw a line of best fit. [1]
(e) Use your line of best fit to estimate a score in the written test for a student who scored 25 in the speaking test.[1]
Answer/Explanation
Ans:
6(a) 4 points correctly plotted
6(b) Positive
6(c) (40, 20) indicated
6(d) Ruled line of best fit
6(e) 33 to 42
Question
(a) On Monday, Main Street station sells 40 tickets.
There are four types of ticket; infant, child, adult and senior.
The bar chart shows the number of infant, child and adult tickets sold.
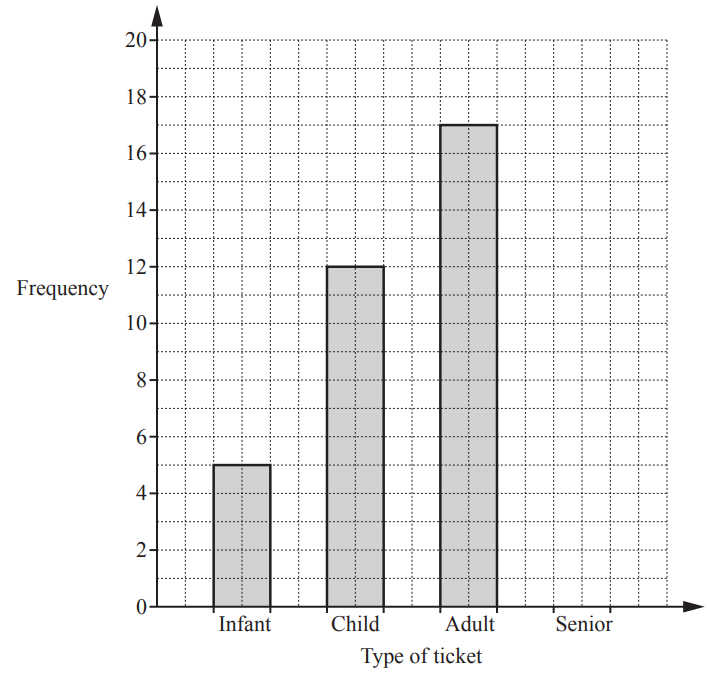
(i) Complete the bar chart. [3]
(ii) Find how many more adult tickets were sold than child tickets.[1]
(iii) Write down the modal type of ticket.[1]
(iv) One of these 40 people is chosen at random.
Find the probability that this person is a child.[1]
(b) At Donville station the number of tickets sold each day is recorded for seven days.
104 18 72 31 27 45 60
Find
(i) the range,[1]
(ii) the median,[2]
(iii) the mean.[2]
Answer/Explanation
Ans:
3(a)(i) Correct bar
3(a)(ii) 5
3(a)(iii) Adult
3(a)(iv) \frac{12}{40} oe
3(b)(i) 86
3(b)(ii) 45
3(b)(iii) 51
Question
(a) 60 boys are asked to name their favourite sport.
The results are shown in the pie chart.
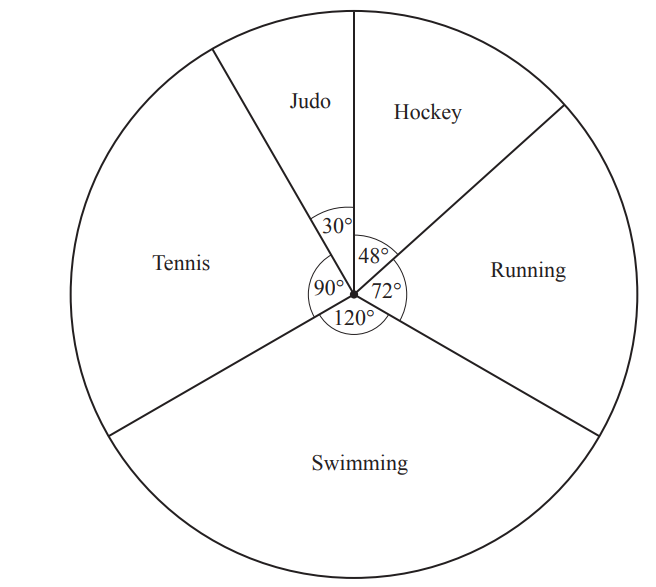
(i) Write down the most popular sport.[1]
(ii) Write down the fraction of boys who choose Running.[1]
(iii) Work out how many boys choose Judo. [2]
(iv) One of the boys is chosen at random.
Work out the probability that his favourite sport is not Judo.[1]
(v) Complete this statement.
Three times as many boys choose ___ than choose ___ [1]
(b) Two of the boys in part (a) then change their choice from Running to Swimming.
Complete the pie chart after this change.
The Tennis, Judo and Hockey sectors have been drawn for you.[2]

(c) 60 girls are asked to name their favourite sport.
Their results are shown in the bar chart below.
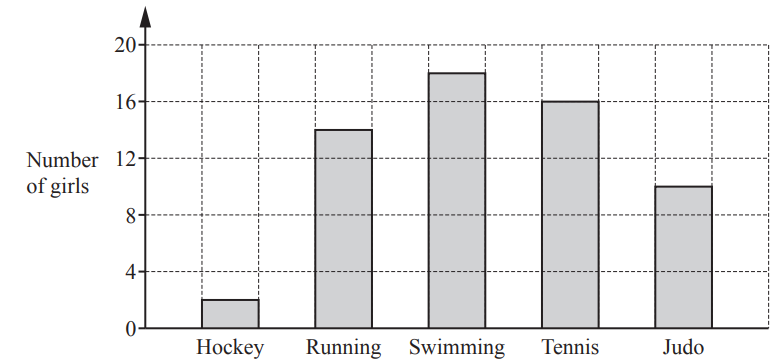
Using your pie chart in part (b) and the bar chart above, write down one similarity and one difference between the girls’ results and the boys’ results.[2]
Similarity
Answer/Explanation
Ans:
1(a)(i) Swimming
1(a)(ii) \(\frac{72}{360}\) oe
1(a)(iii) 5 cao
1(a)(iv) \(\frac{55}{60}\) oe
1(a)(v) Tennis, Judo
1(b) 2 sectors drawn:
Running 60°
Swimming 132°
1(c) A valid correct similarity and difference
Question
(a) 20 students from College A each run 5km. The times, correct to the nearest minute, are recorded.
32 51 25 40 47 21 37 32 48 36
46 39 30 29 44 39 53 35 40 31
(i) Complete the stem-and-leaf diagram.

(ii) Find the range of the times.
…………………………………… min
(iii) Find the median of the times.
…………………………………… min
(iv) Complete the bar chart for the times of the students.
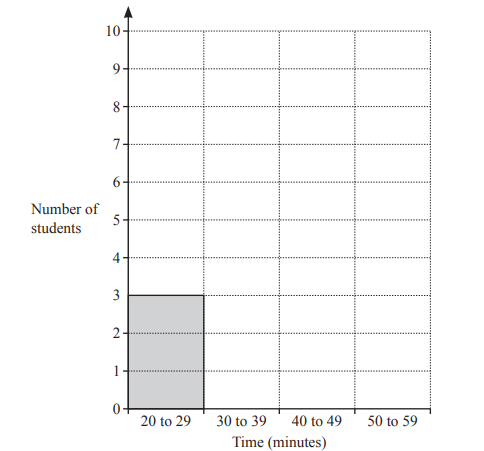
b) 20 students from College B each run 5km.
Their times, correct to the nearest minute, are recorded and the results are shown in the table.
(i) Complete the table.
(ii) Complete the pie chart.
(c) Write down two comments comparing the times of students from College A with the times of
students from College B. ………………………………………………………………………………………………………………………………..
……………………………………………………………………………………………………………………………….. ………………………………………………………………………………………………………………………………..
………………………………………………………………………………………………………………………………..
Answer/Explanation
(a)(i) [2] 1 5 9
[3] 0 1 2 2 5 6 7 9 9
[4] 0 0 4 6 7 8
[5] 1 3
(ii) 32
(iii) 38
(iv) Correct bar chart
(b)(i) 144
126
(ii) Correct pie chart
(c) 2 correct expressions
Question
(a) The scale drawing shows the positions of a rock, R, and a statue, S, on a map.
The scale is 1 centimetre represents 6 metres.
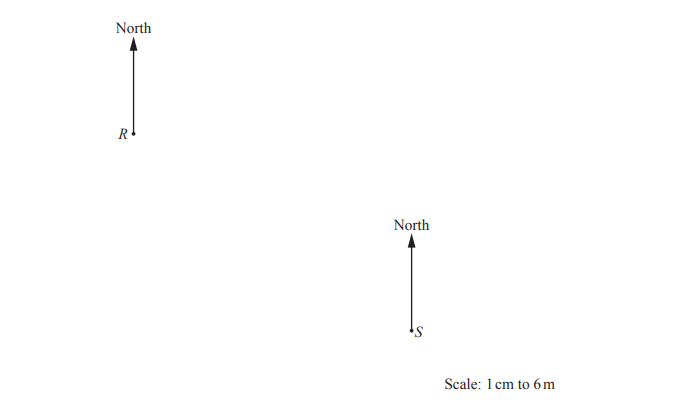
(i) Work out the actual distance between R and S.
……………………………………… m
(ii) A flagpole, F, is on a bearing of 164° from S.
Work out the bearing of S from F.
………………………………………….
(iii) Ishaan uses the map to find some treasure, T.
T is on a bearing of 076° from R and on a bearing of 337° from S.
Mark the position of T on the map.
(b) The treasure is a bag of coins.
The coins are made from three different metals.
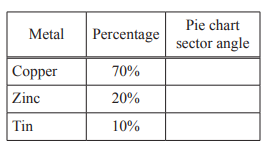
(i) Complete the table.
(ii) Complete the pie chart.
Answer/Explanation
(a))(i) 54
(ii) 344
(iii) T marked correctly
(b)(i) 252, 72, 36
(ii) Correct pie chart drawn
Question
20 students choose their favourite science subject.
The results are shown in the bar chart.
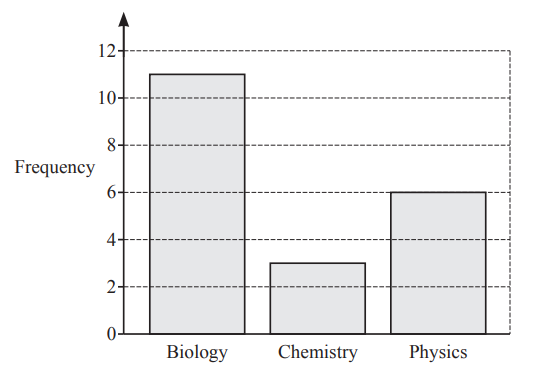
(a) Work out how many more students choose biology than physics.
………………………………………….
(b) Write down the fraction of students whose favourite science subject is chemistry.
………………………………………….
(c) One of the 20 students is picked at random.
Write down the probability that this student did not choose biology.
………………………………………….
(d) Only one of the averages, median, mode and mean can be found for these results.
(i) Write down the average that can be found.
………………………………………….
(ii) Find this average for these results.
………………………………………….
(iii) Explain why the range cannot be found.
……………………………………………………………………………………………………………………………
(e) The results are to be shown in a pie chart.
(i) Complete the table,
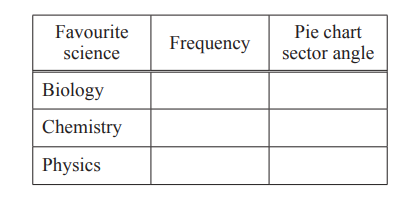
(ii) Complete the pie chart.
Answer/Explanation
(a) 5
(b)\(\frac{3}{20}\)
(c)\(\frac{9}{20}\)
(d)(i) Mode
(ii) Biology
(iii) Correct reason
(e)(i) 11 198
3 54
6 108
(ii) Correct pie chart drawn
Question
20 students choose their favourite science subject.
The results are shown in the bar chart.

(a) Work out how many more students choose biology than physics.
………………………………………….
(b) Write down the fraction of students whose favourite science subject is chemistry.
………………………………………….
(c) One of the 20 students is picked at random.
Write down the probability that this student did not choose biology.
………………………………………….
(d) Only one of the averages, median, mode and mean can be found for these results.
(i) Write down the average that can be found.
………………………………………….
(ii) Find this average for these results.
………………………………………….
(iii) Explain why the range cannot be found.
……………………………………………………………………………………………………………………………
(e) The results are to be shown in a pie chart.
(i) Complete the table,

(ii) Complete the pie chart.

Answer/Explanation
(a) 5
(b)\(\frac{3}{20}\)
(c)\(\frac{9}{20}\)
(d)(i) Mode
(ii) Biology
(iii) Correct reason
(e)(i) 11 198
3 54
6 108
(ii) Correct pie chart drawn
Question
(a) Jon spins this 6-sided spinner.
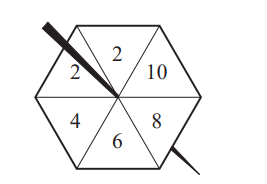
The probability that the spinner lands on any of the six sides is equally likely.
Write down the probability that the spinner lands on
(i) the number 6,
Answer/Explanation
Ans: \(\frac{1}{6}oe\)
(ii) a prime number,
Answer/Explanation
Ans: \(\frac{2}{6}oe\)
(iii) a number less than 11.
Answer/Explanation
Ans: 1
(b) Felix has a 12-sided spinner with the numbers 2, 4, 5, 7 and 9 written on it.
It is equally likely to land on any side.
The table shows the probability of the spinner landing on each number.

The diagram of the spinner has been completed for the number 2.
Complete the diagram for the numbers 4, 5, 7 and 9.
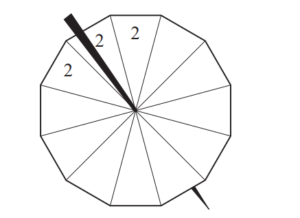
Answer/Explanation
Ans: (2,2,2), 4,4,4,4,5,5,7,7,9 seen on spinner
(c) Felix says that his spinner is more likely to land on a 2 than Jon’s spinner.
Explain why he is wrong.
Answer/Explanation
Ans: Felix’s probability is \(\frac{3}{12}\) which is
less than Jon’s probability \(\left (of\frac{2}{6} \right )\) which is \(\frac{4}{12}oe\)
(d) Felix spins his 12-sided spinner 60 times and records the results.
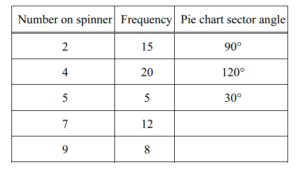
(i) Complete the table by working out the sector angles for the numbers 7 and 9 .
Answer/Explanation
Ans: (90°, 120°, 30°), 72°, 48°
(ii) Complete the pie chart.
Answer/Explanation
Ans: 30° angle correct 72°, 48°
(iii) Write down the mode.
Answer/Explanation
Ans: 4
(iv) Calculate the mean.
Answer/Explanation
Ans: 4.85
Question
(a) Amir asked 15 friends how many hours they spent playing sport last weekend. His results are shown in the table below.

(i) Write down the mode.
Answer/Explanation
Ans: 0
(ii) Find the median.
Answer/Explanation
Ans: 1
(iii) Calculate the mean.
Answer/Explanation
Ans: 1.6
(iv) On the grid, draw a bar chart to show the information given in the table.
Answer/Explanation
Ans: Bar chart with
– horizontal axis correctly labelled
– and vertical axis correctly scaled
– and bars of correct height and equal width,
– and with equal gaps or no gaps
(b) Amir also asked these 15 friends which was their favourite sport. His results are shown in the table below.
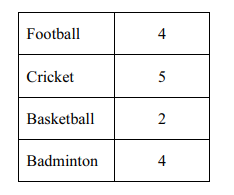
Amir picks one of these friends at random. Write down the probability that his friend’s favourite sport is
(i) cricket,
Answer/Explanation
Ans: \(\frac{5}{15}or\frac{1}{3}\)
(ii) not football,
Answer/Explanation
Ans: \(\frac{11}{15}\)
(iii) basketball or badminton.
Answer/Explanation
Ans: \(\frac{6}{15}or\frac{2}{5}\)
Question
Twelve students each answer 30 questions in a quiz.
The time taken and the number of correct answers for each student is given in the table.

(a) Complete the scatter diagram below to show this information. The first six points have been plotted for you.
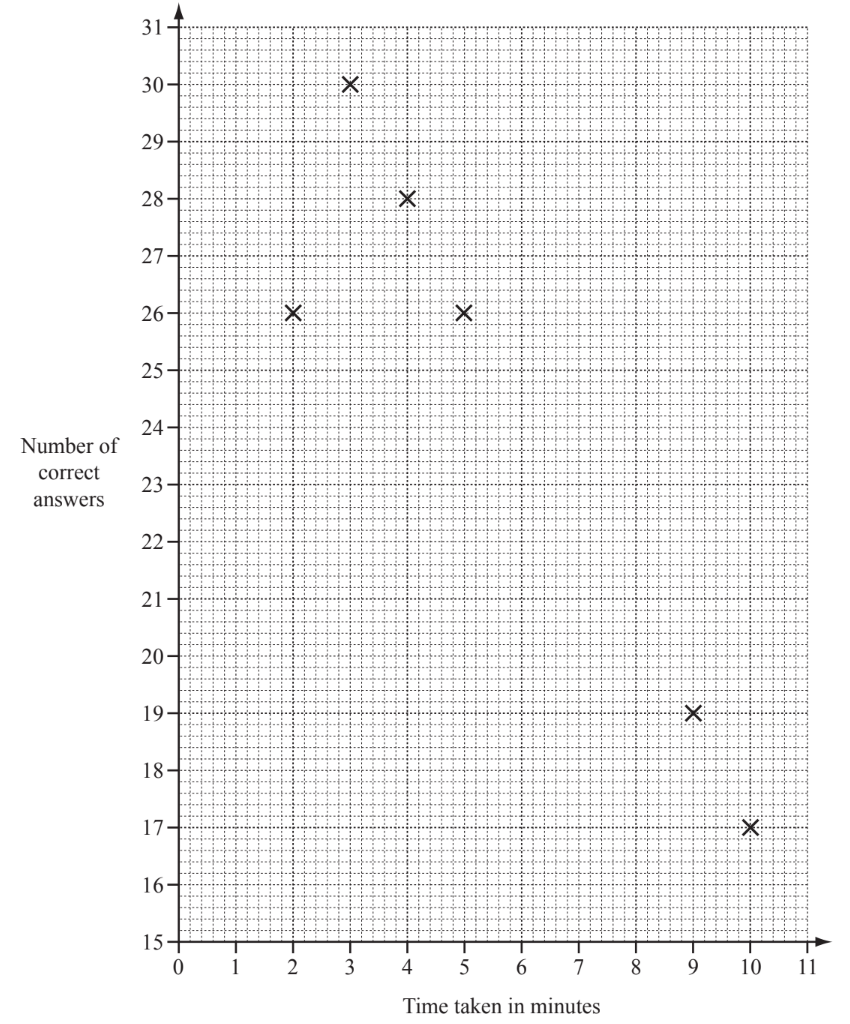
(b) What type of correlation does the scatter diagram show?
(c) (i) Find the range of the time taken.
(ii) Calculate the mean time taken.
(d) (i) Find the mode for the number of correct answers.
(ii) Find the median for the number of correct answers.
(e) One of the 12 students is selected at random. Write down the probability that the student
(i) took more than 8 minutes to answer the quiz,
(ii) took less than 5 minutes and had more than 24 correct answers.
▶️Answer/Explanation
(a) 6 points correctly plotted
(b) negative cao
(c) (i) $8 \mathrm{cao}$
(ii) $\operatorname{art} 5.92$
(d) (i) $26 \mathrm{cao}$
(ii) 23.5 cao
(e) (i) $\frac{2}{12}$ oe
(ii) $\frac{3}{12}$ oe
Question
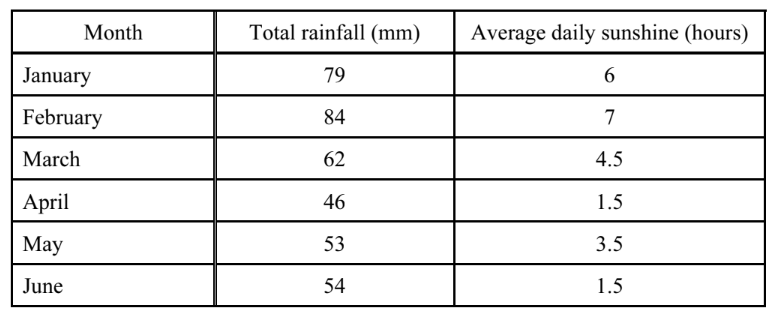
The table shows some data about rainfall and sunshine.
(a) For the rainfall, calculate
(i) the mean,
(ii) the range.
(b) For the sunshine, find
(i) the mode,
(ii) the median.
(c) Dinesh draws a pie chart to display the rainfall data. Calculate the sector angle for February.
(d) Amalia draws a pictogram to display the sunshine data for January and February.
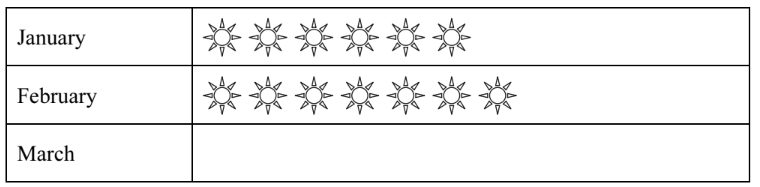
(i) Complete the key for the pictogram.
(ii) Complete the pictogram for March.
(e) Priya draws a scatter diagram to find the correlation between rainfall and sunshine for January to June.
(i) Complete the scatter diagram below. January and February are plotted for you.
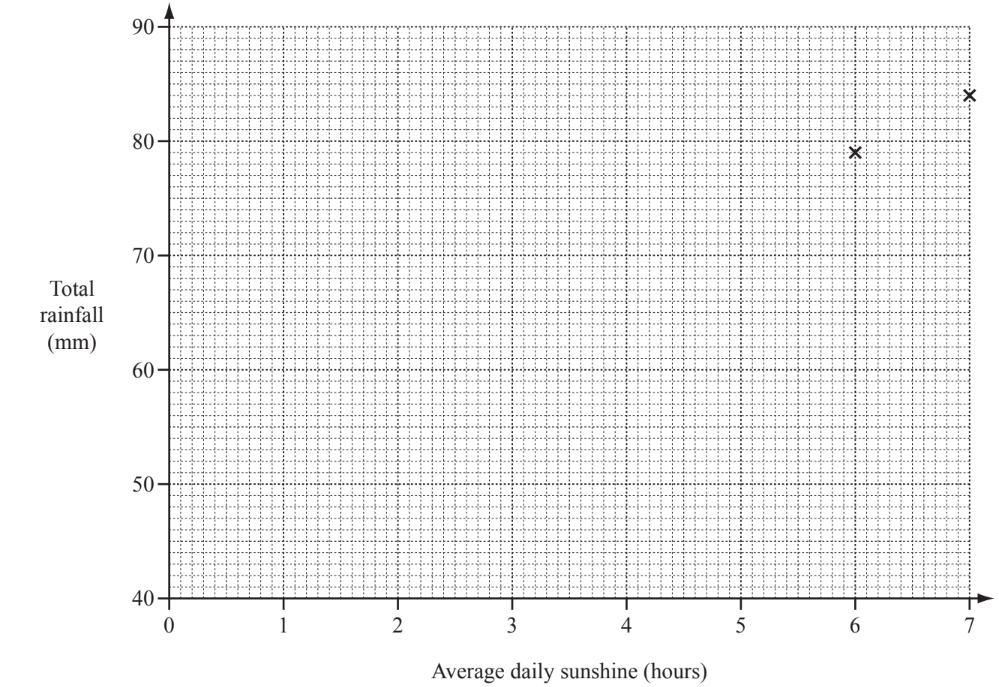
(ii) What type of correlation does the scatter diagram show?
▶️Answer/Explanation
(a) (i) 63
(ii) 38 cao
(b) (i) $1.5 \mathrm{cao}$
(ii) 4
(c) $80^{\circ}$
(d) (i) 1 hour
(ii) 4 and a half more suns drawn
(e) (i) 4 correct plots
(ii) Positive
