Question
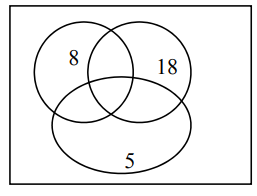
This year, 40 students have each travelled by one or more of plane (P), train (T) or boat (B).
7 have travelled only by plane.
11 have travelled only by train.
9 have travelled only by boat.
\(n(P\cap T) = 8\)
\(n(B\cap T )= 3\)
\(n(B\cap P )= 6\)

(A) Complete the Venn diagram.
(b) Find \(n((P\cup B){}’)\)
………………………………………….
(c) Use set notation to complete the statement.
\(\left ( P \cup T\cup B\right ){}’= ………………………\)
(d) Two students are chosen at random.
Calculate the probability that they both have travelled only by plane.
………………………………………….
(e) Two students are chosen at random from those who have travelled by train.
Calculate the probability that they both have also travelled by plane.
………………………………………….
Answer/Explanation
(a)
(b) 11
(c)\(\phi\) or {}
(d)\(\frac{7}{260}\)
(e)\(\frac{14}{95}\)
Question
x is an integer.
E = \({x : 41\leq x\leq 50}\)
A = {x : x is an odd number}
B = {x : x is a multiple of 3}
C = {x : x is a prime number}
(a) Complete the Venn diagram to show this information.

(b) List the elements of
(i) \(A\cap C,\)
………………………………………….
(ii)\( (B\cup C)’.\)
………………………………………….
(c) Find \(n(A\cap B\cap C).\)
………………………………………….
Answer/Explanation
(a) Correct Venn diagram
(b)(i) 41, 43, 47
(ii) 44, 46, 49, 50
(c) 0
Question
(a) The Venn diagram shows two sets, A and B

(i) Use set notation to complete the statements.
(a) d ___ A [1]
(b) { f, g} = ___ [1]
(ii) Complete the statement.
n ( ___ ) = 6 [1]
(b) In the Venn diagram below, shade C ∩ D’.[1]

(c) 50 students study at least one of the subjects geography (G), mathematics (M) and history (H).
18 study only mathematics.
19 study two or three of these subjects.
23 study geography.
The Venn diagram below is to be used to show this information.

(i) Show that x = 4.[2]
(ii) Complete the Venn diagram. [2]
(iii) Use set notation to complete this statement.
( G ∪ M ∪ H)’ = [1]
(iv) Find n( G ∪ (M ∪ H)).[1]
Answer/Explanation
Ans:
9(a)(i)(a) ∈
9(a)(i)(b) A ∩ B
9(a)(ii) B or A′
9(b)

9(c)(i) 3x+7=19 oe
3x=19-7 or better leading to x = 4
9(c)(ii)
9(c)(iii) ∅ or { }
9(c)(iv) 15