Question
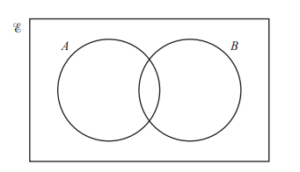
In the Venn diagram shade the region A ∪ B’
Answer/Explanation
Ans: 
Question
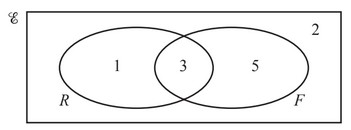
11 students are asked if they like rugby (R) and if they like football (F).
The Venn diagram shows the results.
(a) A student is chosen at random.
What is the probability that the student likes rugby and football?
(b) On the Venn diagram shade the region \(R’ \cap F’\).
Answer/Explanation
Ans:
(a) \(\frac{3}{11}\)
(b) 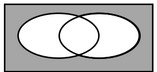
Question
(a) n(\(\xi \)) = 10, n(A) = 7, n(B) = 6, n(\(A \cup B\))’, = 1.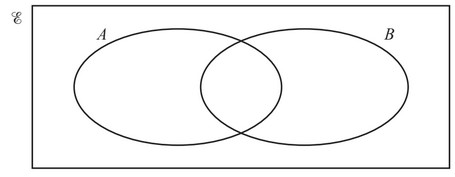
(i) Complete the Venn diagram by writing the number of elements in each subset.
(ii) An element of is chosen at random.
Find the probability that this element is an element of \(A’ \cap B\).
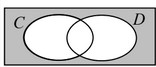
(b) On the Venn diagram below, shade the region \(C’ \cap D’\).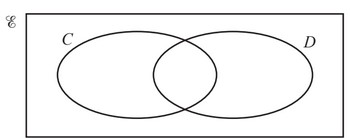
Answer/Explanation
Ans:
(a) (i) 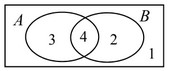
(ii) \(\frac{2}{10}\) oe
(b)