Question
The table below shows the marks scored by a group of students in a test.

(a) Find the mean, median and mode.
(b) The table below shows the time (t minutes) taken by the students to complete the test.

(i) Cara rearranges this information into a new table.
Complete her table.

(ii) Cara wants to draw a histogram to show the information in part (b)(i).
Complete the table below to show the interval widths and the frequency densities.

(c) Some of the students were asked how much time they spent revising for the test.
10 students revised for 2.5 hours, 12 students revised for 3 hours and n students revised for
4 hours.
The mean time that these students spent revising was 3.1 hours.
Find n.
Show all your working.
▶️Answer/Explanation
(a) Mean=\(\sum\frac{x_if_i}{f_i}\)

Now, \(\sum{x_i f_i}\)=1071
\(\sum{ f_i}\)=75
So, Mean= \(\frac{1071}{75}\)
=14.28
Question
The table below shows the marks scored by a group of students in a test.

(a) Find the mean, median and mode.
(b) The table below shows the time (t minutes) taken by the students to complete the test.

(i) Cara rearranges this information into a new table.
Complete her table.

(ii) Cara wants to draw a histogram to show the information in part (b)(i).
Complete the table below to show the interval widths and the frequency densities.

(c) Some of the students were asked how much time they spent revising for the test.
10 students revised for 2.5 hours, 12 students revised for 3 hours and n students revised for
4 hours.
The mean time that these students spent revising was 3.1 hours.
Find n.
Show all your working.
Answer/Explanation
(a)
\(\Rightarrow\) Mean=\(\sum\frac{x_if_i}{f_i}\)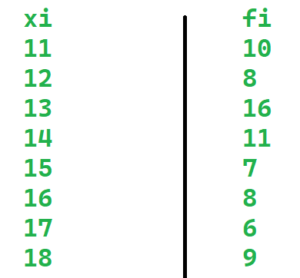
Now, \(\sum{x_i f_i}\)=1071
\(\sum{ f_i}\)=75
So, Mean= \(\frac{1071}{75}\)
=14.28
\(\Rightarrow\) Median = Lower boundary of the interval + [(N/2 – Cumulative frequency of the preceding interval) / Frequency of the interval] * Interval width
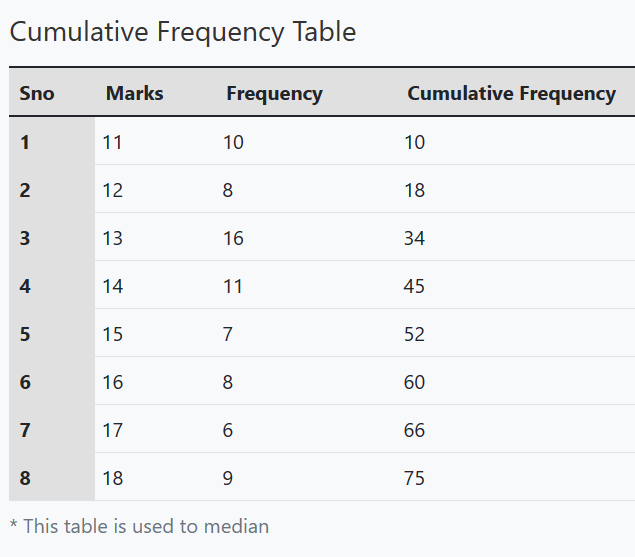
To find the median:
Total number of values = 75 (odd)
Median position =\(\frac{(75 + 1)} {2}\) = 38th position
As 38th position falls in the interval with a mark of 14 and a cumulative frequency of 45, we can calculate median as follows:
Interval width = 1
Median = 14 + \(\frac{(38 – 34)}{11} \times 1 \) = 14 + \(\frac{4}{11}\) = 14 + 0.3636 = 14.3636 \(\approx \) 14.
Median = 14.
\(\Rightarrow\) Mode = Marks with highest frequency
From the table, we can see that the value 13 appears most frequently with a frequency of 16. So, the mode of the given data set is 13.
Mode = 13.
(b) (i)

(ii)
HISTROGRAM:
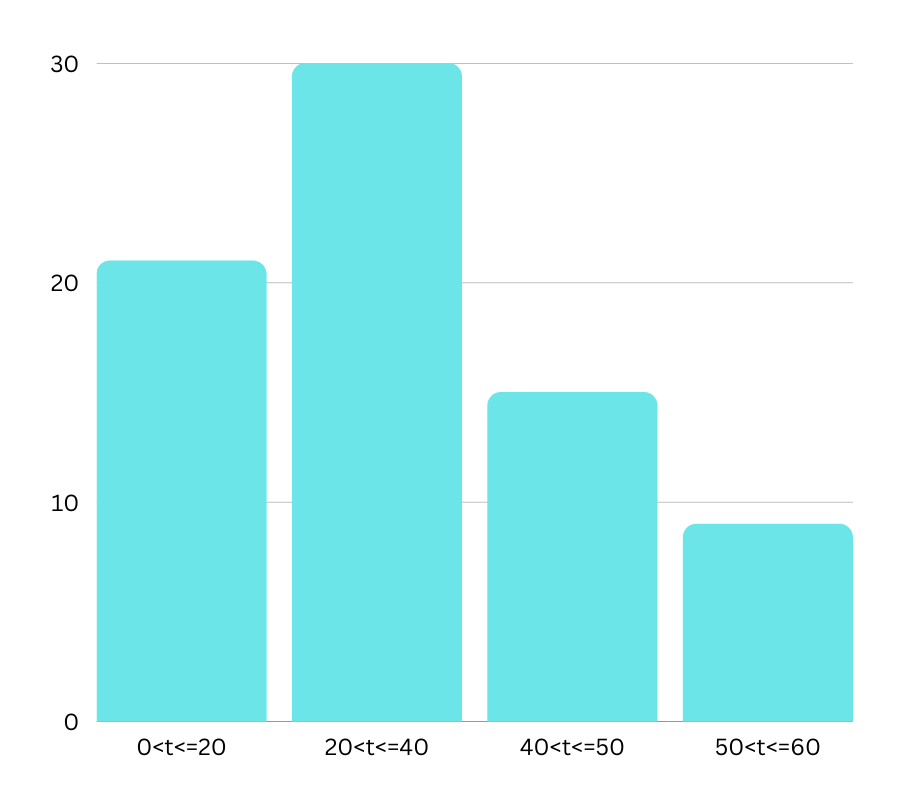
The completed table of the interval widths and the frequency densities are as follows:
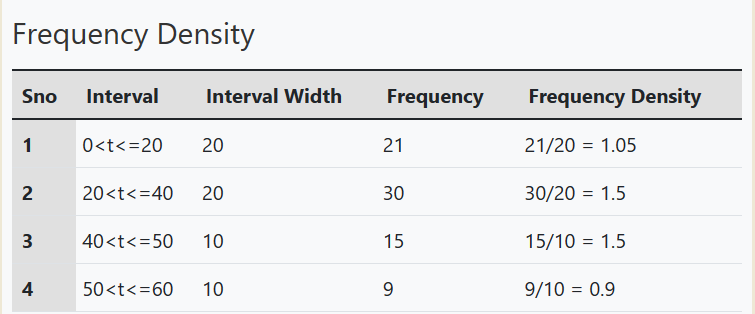
(c)
Total time = (10 students \(\times\)2.5 hours) + (12 students \(\times\) 3 hours) + (n students \(\times\) 4 hours) = 25 + 36 + 4n = 61 + 4n.
Given : Mean Time spent revising = 3.1 hours
Using Formula: Mean time = Total time / Total number of students
\(\Rightarrow\) 3.1 = \(\frac{(61 + 4n)} {(10 + 12 + n)}\)
\(\Rightarrow\) 3.1 = \(\frac {(61 + 4n)}{(22 + n)}\)
\(\Rightarrow\) 3.1 . (22 + n) = 61 + 4n
\(\Rightarrow\) 68.2 + 3.1n = 61 + 4n
\(\Rightarrow\) 3.1n – 4n = 61 – 68.2
\(\Rightarrow\) -0.9n = -7.2
\(\Rightarrow\) n =\(\frac{ -7.2}{-0.9}\)
\(\Rightarrow\) n = 8
Therefore,the value of n is 8.
Question
Mr Chang hires x large coaches and y small coaches to take 300 students on a school trip.
Large coaches can carry 50 students and small coaches 30 students.
There is a maximum of 5 large coaches.
(a) Explain clearly how the following two inequalities satisfy these conditions.
(i)\( x\leq 5\)
(ii) \(5x + 3y\geq 300\)
Mr Chang also knows that \(x + y\leq10\)
(b) On the grid, show the information above by drawing three straight lines and shading the
unwanted regions.
(c) A large coach costs \(\$450\)to hire and a small coach costs \(\$350\)
(i) Find the number of large coaches and the number of small coaches that would give the
minimum hire cost for this school trip.
(ii) Calculate this minimum cost.
Answer/Explanation
(a) (i) There are up to 5 large coaches
(ii) There are 50 in large coaches and 30 in small coaches which must be equal to 300 seats or more.
(b) 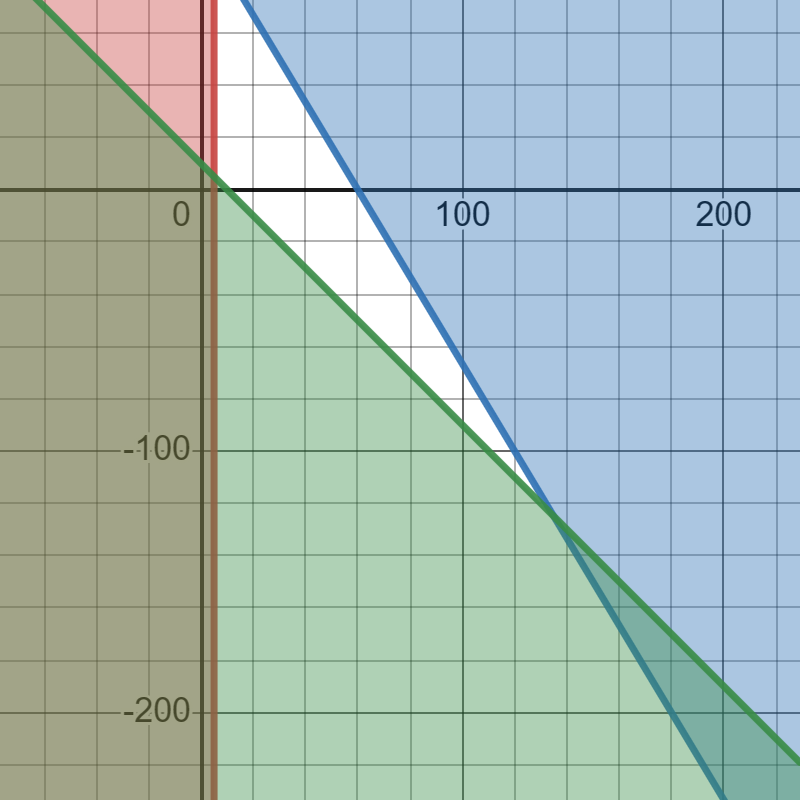
Blue shade: \(5x + 3y\geq 300\)
Green shade: \(x + y\leq10\)
Red shade: \( x\leq 5\)
(c)(i) \(\frac{5}{2}\)
(ii) 2950