Question
Dhanu has a model railway.
(a) He has a train that consists of a locomotive and 4 coaches.
The mass of the locomotive is 87g and the mass of each coach is 52g.
(i) Work out the total mass of the train.
………………………………………. g
(ii) Work out the mass of the locomotive as a percentage of the total mass of the train.
……………………………………… %
(b) The train is 61cm long and travels at a speed of 18cm/s.
It takes 4 seconds for the whole of the train to cross a bridge.
Calculate the length of the bridge.
……………………………………. cm
(c) A new locomotive costs \($64.\)
Calculate the cost of the locomotive in rupees when the exchange rate is 1 rupee = \($0.0154 .\)
Give your answer correct to the nearest 10 rupees.
……………………………….. rupees
(d) The cost of a railway magazine increases by 12.5% to \($2.70 .\)
Calculate the cost of the magazine before this increase.
\($ ………………………………………….\)
(e) Dhanu plays with his model railway from 0650 to 11 15.
He then rides his bicycle for 3 hours.
Find the ratio time playing with model railway : time riding bicycle.
Give your answer in its simplest form.
……………………. : …………………….
(f) The value of Dhanu’s model railway is \($550.\)
This value increases exponentially at a rate of r% per year.
At the end of 5 years the value will be \($736.\)
Calculate the value of r.
r = ………………………………………….
Answer/Explanation
(a)(i) 295
(a)(ii) 29.5 or 29.49…
(b) 11
(c) 4160
(d) 2.4[0]
(e) 53 : 36
(f) 6[.00] or 5.999…
Question
(a) Davinder asked some people if they ate mangoes, pineapples or bananas last week.
M = { people who ate mangoes }
P = { people who ate pineapples }
B = { people who ate bananas }
The Venn diagram shows some of the information.
19 people said they ate mangoes.
6 people said they ate only pineapples.
18 people said they ate exactly two of the three types of fruit.
(i) Write the three missing values in the Venn diagram.
(ii) Find the total number of people Davinder asked.
(iii) Find n(M\(\cup \) P).
(iv) One person is chosen at random from the people who ate mangoes.
Write down the probability that this person also ate bananas.
(b) Davinder draws a speed-time graph for his bus journey to the market.
Find
(i) the acceleration of the bus during the first 200 seconds,
………………………….. \(m/s^2\)
(ii) the total distance travelled by the bus,
……………………………. m
(iii) the average speed of the bus for the whole journey.
……………………………………. m/s
Answer/Explanation
Ans:
(a) (i) 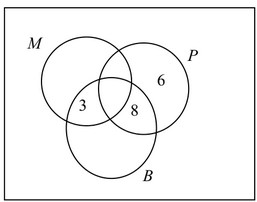
(ii) 46
(iii) 11
(iv) \(\frac{7}{19}\) oe
(b) (i) \(\frac{9}{200}\) or 0.045
(ii) 10800
(iii) 7.2
Question
(a) 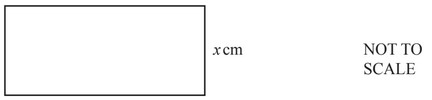
The perimeter of the rectangle is 80cm.
The area of the rectangle is A\(cm^2\).
(i) Show that \(x^2 – 40x + A = 0\)
(ii) When A = 300, solve, by factorising, the equation \(x^2 – 40x + A = 0\)
(ii) When A = 300, solve, by factorising, the equation \(x^2 – 40x + A = 0\)
x = …………………….. or x = ……………………………
(iii) When A = 200, solve, by using the quadratic formula, the equation \(x^2 – 40x + A = 0\).
Show all your working and give your answers correct to 2 decimal places.
x = ………………… or x = ………………..
(b) A car completes a 200km journey with an average speed of xkm/h.
The car completes the return journey of 200km with an average speed of (x + 10) km/h.
(i) Show that the difference between the time taken for each of the two journeys is \(\frac{2000}{x(x+10)}\) hours.
(ii) Find the difference between the time taken for each of the two journeys when x = 80.
Give your answer in minutes and seconds.
…………………. min ………………. s
Answer/Explanation
Answer:
(a) (i) \([y=] \frac{1}{2}(80-2x)\)
A = their \(\frac{1}{2}(80-2x) \times x\) oe
A = \(40x – x^2\) and \(x^2 – 40x + A = 0\)
(ii) (x – 30)(x – 10)
30, 10
(iii) \(\sqrt{(-40)^2 -4(1)(200)}\) or better
P = — 40 and r = 2(1)
5.86
34.14
(b) (i) \(\frac{200}{x} – \frac{200}{x+10}\)
\(\frac{200(x+10)-200x}{x(x+10)} = \frac{2000}{x(x+10)}\)
(ii) 16 [min] 40 [s]