Question
(a) The table shows some values for \(y=2x^{3}-4x^{2}+3.\)

(i) Complete the table.
(ii) On the grid, draw the graph of \(y=2x^{3}-4x^{2}+3\) for \(-1\leq x\leq 2.\)

(iii) Use your graph to solve the equation \(2x^{3}-4x^{2}+3=1.5\)
x = …………………… or x = …………………… or x = ……………………
(iv) The equation \(2x^{3}-4x^{2}+3=k\) has only one solution for \(-1\leq k\leq 2.\)
Write down a possible integer value of k.
………………………………………….
(b)
(i) On the grid, draw the tangent to the curve at x = 1.
(ii) Use your tangent to estimate the gradient of the curve at x = 1.
………………………………………….
(iii) Write down the equation of your tangent in the form y=mx+c
y = ………………………………………….
Answer/Explanation
(a)(i) 3 2.25 1
(ii) Fully correct smooth curve
(iii) −0.6 to −0.51, 0.75 to 0.85,
1.7 to 1.85
(iv) −3 or −2 or −1 or 0
(b)(i) Tangent ruled at x = 1
(ii) 4.4 to 5.6
(iii) y = (4.4 to 5.6)x – (1.8 to 2.2)
Question
(a) Solve the equation tan x = 11.43 for \(0\leqslant x\leqslant 360^{\circ}\)
(b) Sketch the curve \(y=x^{3}-4x\)
(c) A curve has equation \(y=x^{3}+ax+b\)
The stationary points of the curve have coordinates (2, k) and (-2, 10 – k).
Work out the value of a, the value of b and the value of k.
Answer/Explanation
12(a) 85[.0], 265[.0] and no others
12(b) 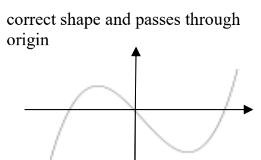
12(c) a = –12
b = 5
k = –11
Question
The table shows some values for \(y=x^{2}-\frac{1}{3x},x\neq 0\)
The y-values are rounded to 1 decimal place.

(a) Complete the table.
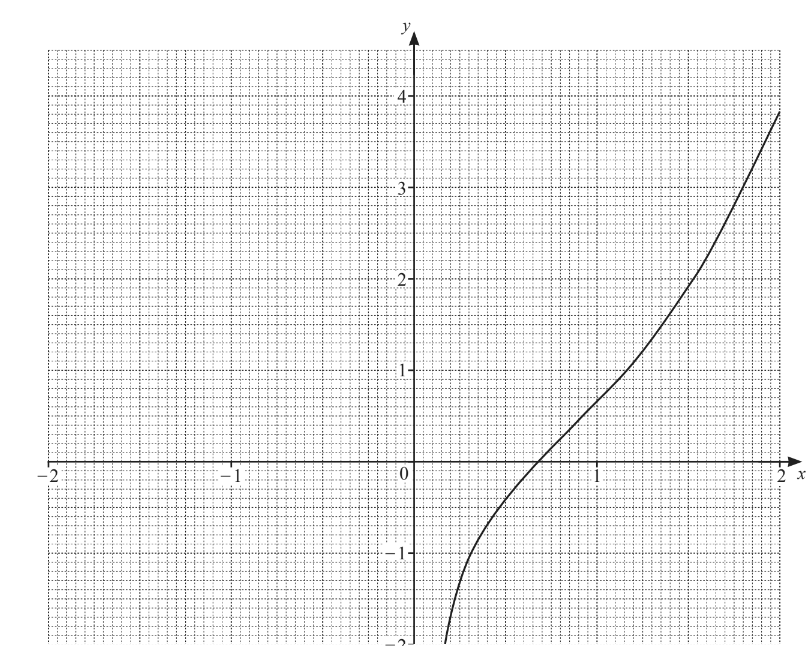
(b) On the grid, draw the graph of \( y=x^{2}-\frac{1}{3x} \)for
\(-2\leqslant x\leqslant -0.1\) The graph of \( y=x^{2}-\frac{1}{3x} \) for x> 0 has been drawn for you.
(c) By drawing a suitable line on the grid, solve the equation \(y=x^{2}-\frac{1}{3x} +1=0\)
Answer/Explanation
(a) 1[.0] 0.9
(b) correct curve
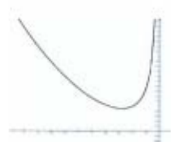
(c) ruled line at y = − 1
0.3 to 0.32