Question
(a) The diagram shows a circle with two chords, AB and CD, intersecting at X.

(i) Show that triangles ACX and DBX are similar
Answer/Explanation
Ans:
Any two of with conclusion
Angle ACD = angle ABD
Angle CAB = angle CDB
Angle AXC = angle DXB
AND
‘triangles have equal angles’ oe
OR
All three of without
conclusion
Angle ACD = angle ABD
Angle CAB = angle CDB
Angle AXC = angle DXB
(ii) AX = 3.2cm, BX = 12.5cm, CX = 4 cm and angle AXC = 110°.
(a) Find DX.
Answer/Explanation
Ans: 10
(b) Use the cosine rule to fi nd AC.
Answer/Explanation
Ans: 42 + 3.22 – 2 × 4 × 3.2cos110
34.9 to 35
5.92 or 5.915 to 5.916
(c) Find the area of triangle BXD.
Answer/Explanation
Ans: 58.7 or 58.73[…]
(b) 
In the diagram, BC represents a building 30m tall.
A flagpole, DC, stands on top of the building.
From a point, A, the angle of elevation of the top of the building is 31°.
The angle of elevation of the top of the fl agpole is 37°.
Calculate the height, DC, of the fl agpole.
Answer/Explanation
Ans: 7.62 or 7.623 to 7.624
Question
(a) 
In the pentagon ABCDE, angle EAB = angle ABC = 110° and angle CDE = 84°.
Angle BCD = angle DEA = x°.
(i) Calculate the value of x.
(ii) BC = CD.
Calculate angle CBD.
(iii) This pentagon also has one line of symmetry.
Calculate angle ADB.
(b) A, B and C lie on a circle centre O.
Angle AOC = 3y° and angle ABC = (4y + 4)°.
Find the value of y.
(c) 
In the cyclic quadrilateral PQRS, angle SPQ = 78°.
(i) Write down the geometrical reason why angle QRS = 102°.
(ii) Angle PRQ:Angle PRS = 1:2.
Calculate angle PQS.
(d)
The diagram shows two similar fi gures.
The areas of the fi gures are 5 \(cm^2\) and 7.2\(cm^2\).
The lengths of the bases are l cm and 6.9cm.
Calculate the value of l.
Answer/Explanation
Answer:
(a) (i) 118
(ii) 31
(iii) 22
(b) 32
(c) (i)
Opposite angles [cyclic quad] add to 180
(ii) 68
(d) 5.75
Question

The quadrilateral ABCD represents an area of land.
There is a straight road from A to C.
AB = 79m, AD = 120m and CD = 95m.
Angle BCA = 26° and angle CDA = 77°.
(a) Show that the length of the road, AC, is 135m correct to the nearest metre.
(b) Calculate the size of the obtuse angle ABC.
(c) A straight path is to be built from B to the nearest point on the road AC.
Calculate the length of this path.
d) Houses are to be built on the land in triangle ACD.
Each house needs at least \(180{m}^2\)
of land.
Calculate the maximum number of houses which can be built.
Show all of your working
Answer/Explanation
(a) To solve this, we can use the law of cosines for finding the length of AC:
\( {AC}^2 = {AB}^2 +{BC}^2\)- 2.AB.BC.Cos(BCA)
For BC, we can use the law of sines
\(\frac{BC}{\sin(BCA)}\)
= \(\frac{CD}{\sin(CAD)}\)
Plugging in the given values, we get:
\({AC}^2 =\frac{{79}^2+{95}^2}{{Sin}^2(26)}\)
=135(rounded to the nearest metre)
(b) 48.5
(c) 30.2
(d) Maximum number of houses : \(\frac{Area}{180}\)
=\(\frac{\frac{1}{2}\times 120 \times 95 \times \sin(77)}{180}\)
=30.8
Question

The quadrilateral ABCD represents an area of land.
There is a straight road from A to C.
AB = 79m, AD = 120m and CD = 95m.
Angle BCA = 26° and angle CDA = 77°.
(a) Show that the length of the road, AC, is 135m correct to the nearest metre.
(b) Calculate the size of the obtuse angle ABC.
(c) A straight path is to be built from B to the nearest point on the road AC.
Calculate the length of this path.
d) Houses are to be built on the land in triangle ACD.
Each house needs at least \(180{m}^2\)
of land.
Calculate the maximum number of houses which can be built.
Show all of your working
Answer/Explanation
(a) To solve this, we can use the law of cosines for finding the length of AC:
\( {AC}^2 = {AB}^2 +{BC}^2\)- 2.AB.BC.Cos(BCA)
For BC, we can use the law of sines
\(\frac{BC}{\sin(BCA)}\)
= \(\frac{CD}{\sin(CAD)}\)
Plugging in the given values, we get:
\({AC}^2 =\frac{{79}^2+{95}^2}{{Sin}^2(26)}\)
=135(rounded to the nearest metre)
(b) 48.5
(c) 30.2
(d) Maximum number of houses : \(\frac{Area}{180}\)
=\(\frac{\frac{1}{2}\times 120 \times 95 \times \sin(77)}{180}\)
=30.8
Question
(a)

The diagram shows a toy boat. AC = 16.5 cm, AB = 19.5 cm and PR = 11 cm. Triangles ABC and PQR are similar.
(i) Calculate PQ.
(ii) Calculate BC.
(iii) Calculate angle ABC.
(iv) The toy boat is mathematically similar to a real boat. The length of the real boat is 32 times the length of the toy boat. The fuel tank in the toy boat holds 0.02 litres of diesel. Calculate how many litres of diesel the fuel tank of the real boat holds.
(b)

The diagram shows a field $D E F G$, in the shape of a quadrilateral, with a footpath along the diagonal $D F$. $D F=105 \mathrm{~m}$ and $F G=67 \mathrm{~m}$. Angle $E D F=70^{\circ}$, angle $E F D=32^{\circ}$ and angle $D F G=143^{\circ}$.
(i) Calculate $D G$.
(ii) Calculate EF.
▶️Answer/Explanation
(a) (i) 13 cao www
(ii) 10.39 to $10.4 \mathrm{wWW}$
(iii) 57.76 to 57.81 www
(iv) 655 to 655.4
(b) (i) 163.5 to $164 \mathrm{www}$
(ii) 100.8 to 100.9 or $101 \mathrm{www}$
Question
(a)
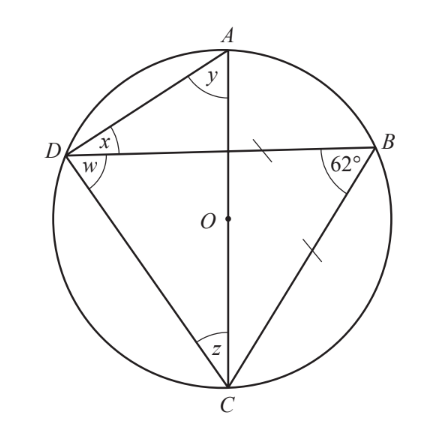
A, B, C and D are points on the circumference of a circle centre O. AC is a diameter. BD = BC and angle DBC = 62U. Work out the values of w, x, y and z. Give a reason for each of your answers.
w = because
x = because
y = because
z = because
(b)

(i) Write down as a column vector.
(ii) $\overrightarrow{A C}=\left(\begin{array}{l}0 \\ 7\end{array}\right)$.
Work out $\overrightarrow{B C}$ as a column vector.
(c)

$\overrightarrow{O R}=\mathbf{r}$ and $\overrightarrow{O T}=\mathbf{t}$.
$P$ is on $R T$ such that $R P: P T=2: 1$.
$Q$ is on $O T$ such that $O Q=\frac{2}{3} O T$.
Write the following in terms of $\mathbf{r}$ and/or $\mathbf{t}$.
Simplify your answers where possible.
(i) $\overrightarrow{Q T}$
(ii) $\overrightarrow{T P}$
(iii) $\overrightarrow{Q P}$
(iv) Write down two conclusions you can make about the line segment QP.
▶️Answer/Explanation
(a) $w=59$
(angle in) isosceles (triangle)
$
x=31
$
(angle in) semicircle $(=90)$ oe
$
y=62
$
(angles in) same segment or (on) same arc $($ are $=$ )
$z=28$
(angles in) triangle $(=180)$
(b) (i) $\left(\begin{array}{l}2 \\ 3\end{array}\right)$
(ii) $\left(\begin{array}{r}-2 \\ 4\end{array}\right)$
(c) (i) $\frac{1}{3} \mathbf{t}$ final answer
(ii) $\frac{1}{3}(-\mathbf{t}+\mathbf{r})$ final answer
(iii) $\frac{1}{3} \mathbf{r}$ final answer
(iv) $Q P=\frac{1}{3} O R$ oe
$Q P$ is parallel to $O R$ or $\mathbf{r}$