Question
(a)
The diagram shows two straight lines intersecting two parallel lines.
Find the values of a, b and c.
a = …………………………………………
b = …………………………………………
c = …………………………………………
(b)
Points R and S lie on a circle with diameter PQ.
RQ is parallel to PS.
Angle RPQ = 58°.
Find the value of x, giving a geometrical reason for each stage of your working.
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
x = …………………………………………
(c)
Points A, B and C lie on a circle, centre O.
Angle AOC = 142°.
Find the value of y.
y = …………………………………………
Answer/Explanation
(a) 126
54
117
(b) angle [in a] semicircle is 90
Allied, co-interior [add to 180]
or
Angles in triangle [ = 180] and
alternate oe
32
(c) 109
Question
(a) A rectangle measures 8.5cm by 10.7cm, both correct to 1 decimal place.
Calculate the upper bound of the perimeter of the rectangle.
…………………………………….. cm
(b)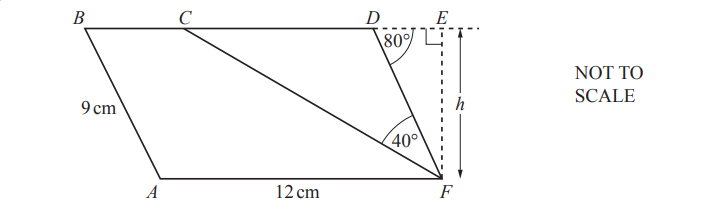
ABDF is a parallelogram and BCDE is a straight line.
AF = 12cm, AB = 9 cm, angle CFD = 40° and angle FDE = 80°.
(i) Calculate the height, h, of the parallelogram.
h = ……………………………………. cm
(ii) Explain why triangle CDF is isosceles.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(iii) Calculate the area of the trapezium ABCF.
(c)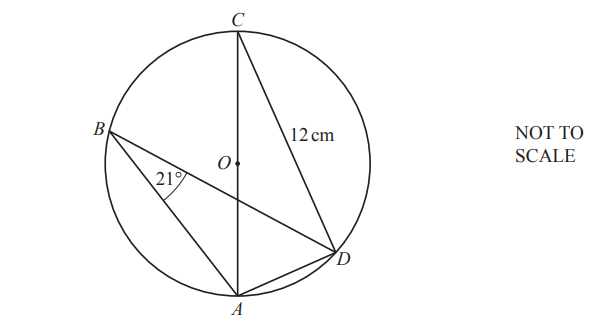
A, B, C and D are points on the circle, centre O.
Angle ABD = 21° and CD = 12 cm.
Calculate the area of the circle.
…………………………………… \(cm^{2}.\)
(d)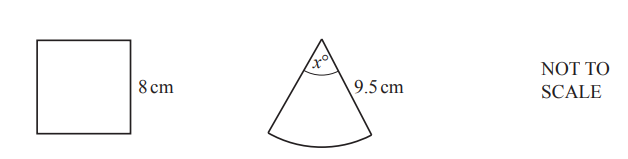
The diagram shows a square with side length 8cm and a sector of a circle with radius 9.5cm
and sector angle x°.
The perimeter of the square is equal to the perimeter of the sector.
Calculate the value of x.
x = …………………………………………
Answer/Explanation
(a) 38.6
(b)(i) 8.86 or 8.863…
(ii) ∠CDF = 100 leading to ∠DCF = 40
Or
∠EDF = 80 leading to ∠DCF = 40
two equal angles’
(iii) 66.5 or 66.45 to 66.47…
(c) 130 nfww or 129.6 to 129.8
(d) 78.4 or 78.37 to 78.41
Question
(a)

In the diagram, AC and BD are straight lines.
Find the value of p and the value of q.[3]
p =
q =
(b) The angles of a quadrilateral are \(x^{\bigcirc },\left ( x+5 \right )^{\bigcirc },\left ( 2x-25 \right )^{\bigcirc } and \left ( x+10 \right )^{\bigcirc }.\)
Find the value of x.
x =[3]
(c) A regular polygon has 72 sides.
Find the size of an interior angle.[3]
(d)

A, B, C and D lie on the circle, centre O, with diameter AC.
PQ is a tangent to the circle at A.
Angle PAD = 60° and angle BAC = 20°.
Find the values of u, v, w, x and y.
u = ____ , v = ____ , w = ____ , x = ____ , y = ____ [6]
(e) A, B and C lie on the circle, center O.
Angle AOC = (3x+22)° and angle ABC = 5x°.
Find the value of x.

x = [4]
Answer/Explanation
Ans:
1(a) [p = ] 132
[q = ] 77
1(b) 74
1(c) 175
1(d) [u = ] 30
[v = ] 60
[w = ] 60
[x = ] 120
[y = ] 40
1(e) 26
Question
(a) The exterior angle of a regular polygon is x° and the interior angle is 8x°.
Calculate the number of sides of the polygon.
…………………………………………
(b)
A, B, C and D are points on the circumference of the circle, centre O.
DOB is a straight line and angle DAC = 58°.
Find angle CDB.
Angle CDB = ……………………………………….
(c)
P, Q and R are points on the circumference of the circle, centre O.
PO is parallel to QR and angle POQ = 48°.
(i) Find angle OPR.
Angle OPR = ………………………………………..
(ii) The radius of the circle is 5.4cm.
Calculate the length of the major arc PQ.
…………………………………… cm
Answer/Explanation
(a) 18
(b) 32
(c)(i) 24
(ii) 29.4 or 29.40 to 29.41
Question

The diagram shows a circle, centre O.
The straight line ABC is a tangent to the circle at B.
OB = 8cm, AB = 15cm and BC = 22.4cm.
AO crosses the circle at X and OC crosses the circle at Y.
(a) Calculate angle XOY.
Angle XOY = ………………………………………..
(b) Calculate the length of the arc XBY.
…………………………………… cm
(c) Calculate the total area of the two shaded regions.
…………………………………. \(cm^{2}\)
Answer/Explanation
(a) 132.26 to 132.28 or 132.3
(b) 18.4 or 18.5 or 18.43 to 18.48
(c) 75.7 to 75.9
Question
(a) 
In the diagram, EH is parallel to FG.
The straight lines EG and FH intersect at Z.
Angle ZFG = 27°.
(i) Find the value of x.
x = …………..
(ii) EH = 5 cm, FG = 9 cm and ZG = 7cm.
Calculate EZ.
EZ = ………………… cm
(b) The diagram shows points A, B, C and D on the circumference of a circle, centre O.
AD is a straight line, AB = BC and angle OAB = 52°.
Find ADC.
Angle ADC = ……………..
(c) The diagram shows points P, Q, R and S on the circumference of a circle, centre O.
VT is the tangent to the circle at Q.
Complete the statements.
(i) Angle QPS = angle QRS = ……………. ° because ………………………………………………………………
(ii) Angle SQP = ……………. ° because ………………………………………………………………………………….
(iii) Part (c)(i) and part (c)(ii) show that
the cyclic quadrilateral PQRS is a …………………………………………….
Answer/Explanation
Answer:
(a) (i) 27
(ii) 3.89 or 3.888 to 3.889
(b) 76 cao
(c) (i) 90
angle in semicircle
(ii) 27
tangent [perpendicular to] radius
(iii) rectangel
Question
2. (a) 
The diagram shows an octagon.
All of the sides are the same length.
Four of the interior angles are each 32°.
The other four interior angles are equal.
Find the value of x.
x = …………………………………………
(b)
P, Q and R lie on a circle, centre O.
Angle PQR = y° and angle POR = (2y – 60)°.
Find the value of y.
y = ……………………………
Answer/Explanation
Ans:
(a) 122
(b) 105
Question
(a) The points A, B, C and D lie on a circle.
AC is a diameter of the circle.
ST is the tangent to the circle at A.

Find the value of
(i) x,
Answer/Explanation
Ans: 42
(ii) y.
Answer/Explanation
Ans: 111
(b) The diagram shows a shaded shape formed by three semi-circular arcs.
The radius of each semi-circle is shown in the diagram.

(i) Calculate the perimeter of the shaded shape.
Answer/Explanation
Ans: 37.7 or 37.69 to 37.704 nfww
(ii) The shaded shape is made from metal 1.6mm thick.
Calculate the volume of metal used to make this shape.
Give your answer in cubic millimetres.
Answer/Explanation
Ans: 12100, 12060, 12070,
12062.4 to 12065.6 nfww
Question
(a) 
In the pentagon ABCDE, angle EAB = angle ABC = 110° and angle CDE = 84°.
Angle BCD = angle DEA = x°.
(i) Calculate the value of x.
(ii) BC = CD.
Calculate angle CBD.
(iii) This pentagon also has one line of symmetry.
Calculate angle ADB.
(b) A, B and C lie on a circle centre O.
Angle AOC = 3y° and angle ABC = (4y + 4)°.
Find the value of y.
(c) 
In the cyclic quadrilateral PQRS, angle SPQ = 78°.
(i) Write down the geometrical reason why angle QRS = 102°.
(ii) Angle PRQ:Angle PRS = 1:2.
Calculate angle PQS.
(d)
The diagram shows two similar fi gures.
The areas of the fi gures are 5 \(cm^2\) and 7.2\(cm^2\).
The lengths of the bases are l cm and 6.9cm.
Calculate the value of l.
Answer/Explanation
Answer:
(a) (i) 118
(ii) 31
(iii) 22
(b) 32
(c) (i)
Opposite angles [cyclic quad] add to 180
(ii) 68
(d) 5.75
Question

The vertices A, B, C, D and E of a regular pentagon lie on the circumference of a circle, centre O, radius 7 cm.
They also lie on the sides of a rectangle WXYZ.
(a) Show that
(i) angle DOC = 72°,
Answer/Explanation
Ans: 360 ÷ 5
(ii) angle DCB = 108°,
Answer/Explanation
Ans: (180 – 72) + 2
54 × 2
(iii) angle CBY = 18°.
Answer/Explanation
Ans: 180 – 90 – 72
(b) Show that the length CD of one side of the pentagon is 8.23 cm correct to three significant figures.
Answer/Explanation
Ans: 2 × 7 × sin(72/2) oe
8.228 to 8.229
(c) Calculate
(i) the area of the triangle DOC,
Answer/Explanation
Ans: 23.3[0..]
(ii) the area of the pentagon ABCDE,
Answer/Explanation
Ans: 116.5 to 116.52 or 117
(iii) the area of the sector ODC,
Answer/Explanation
Ans: 30.78 to 30.8
(iv) the length XY.
Answer/Explanation
Ans: 12.66 to 12.67 or 12.7
(d) Calculate the ratio
area of the pentagon ABCDE: area of the rectangle WXYZ.
Give your answer in the form 1 : n.
Answer/Explanation
Ans: 1.43 or 1.432 to 1.453 cao
Question

A, B, C and D lie on a circle, centre O.
AB = 7 cm, BC = 10 cm and angle ABD = 77°.
AOC is a diameter of the circle.
(a) Find angle ABC.
Answer/Explanation
Ans: 90
(b) Calculate angle ACB and show that it rounds to 35° correct to the nearest degree.
Answer/Explanation
Ans: tan(ACB) = 7 ÷ 10 oe
34.9(9…)
(c) Explain why angle ADB = angle ACB.
Answer/Explanation
Ans: same segment
(d) (i) Calculate the length of AD.
Answer/Explanation
Ans: 11.9 or 11.8(9….) www 3
(ii) Calculate the area of triangle ABD.
Answer/Explanation
Ans: 38.6 (38.58 to 38.62) www 2
(e) The area of triangle AED = 12.3 cm2, correct to 3 significant figures.
Use similar triangles to calculate the area of triangle BEC.
Answer/Explanation
Ans: 8.69 or 8.7(0) or 8.685 to 8.700…. cao
www 3
Question
(a)
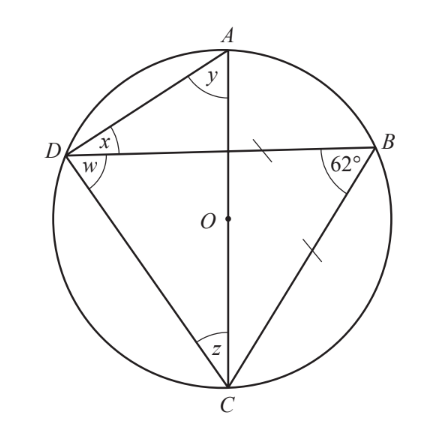
A, B, C and D are points on the circumference of a circle centre O. AC is a diameter. BD = BC and angle DBC = 62U. Work out the values of w, x, y and z. Give a reason for each of your answers.
w = because
x = because
y = because
z = because
(b)

(i) Write down as a column vector.
(ii) $\overrightarrow{A C}=\left(\begin{array}{l}0 \\ 7\end{array}\right)$.
Work out $\overrightarrow{B C}$ as a column vector.
(c)

$\overrightarrow{O R}=\mathbf{r}$ and $\overrightarrow{O T}=\mathbf{t}$.
$P$ is on $R T$ such that $R P: P T=2: 1$.
$Q$ is on $O T$ such that $O Q=\frac{2}{3} O T$.
Write the following in terms of $\mathbf{r}$ and/or $\mathbf{t}$.
Simplify your answers where possible.
(i) $\overrightarrow{Q T}$
(ii) $\overrightarrow{T P}$
(iii) $\overrightarrow{Q P}$
(iv) Write down two conclusions you can make about the line segment QP.
▶️Answer/Explanation
(a) $w=59$
(angle in) isosceles (triangle)
$
x=31
$
(angle in) semicircle $(=90)$ oe
$
y=62
$
(angles in) same segment or (on) same arc $($ are $=$ )
$z=28$
(angles in) triangle $(=180)$
(b) (i) $\left(\begin{array}{l}2 \\ 3\end{array}\right)$
(ii) $\left(\begin{array}{r}-2 \\ 4\end{array}\right)$
(c) (i) $\frac{1}{3} \mathbf{t}$ final answer
(ii) $\frac{1}{3}(-\mathbf{t}+\mathbf{r})$ final answer
(iii) $\frac{1}{3} \mathbf{r}$ final answer
(iv) $Q P=\frac{1}{3} O R$ oe
$Q P$ is parallel to $O R$ or $\mathbf{r}$