Question
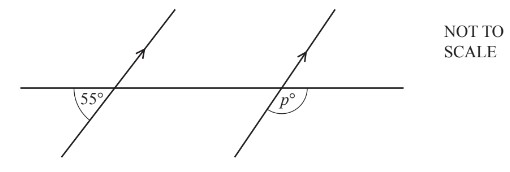
Find the value of p.
Answer/Explanation
Ans:
p = 125
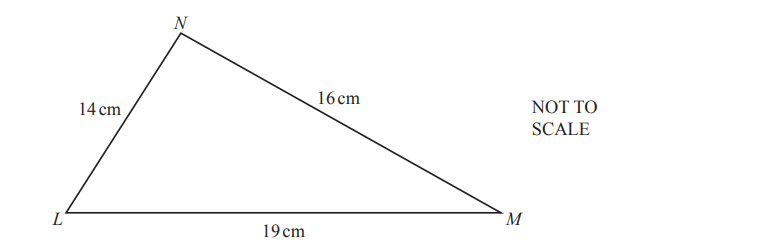
Question
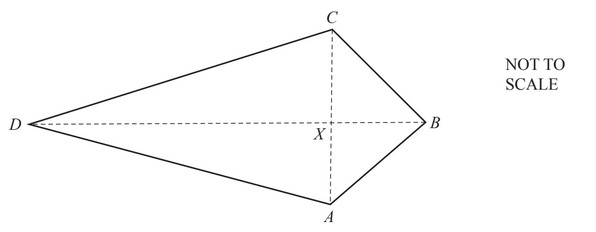
ABCD is a kite.
The diagonals AC and BD intersect at X.
AC = 12cm, BD = 20cm and DX:XB = 3:2 .
(a) Calculate angle ABC.
(b) Calculate the area of the kite.
Answer/Explanation
Ans:
(a) 73.7 or 73.73 to 73.74
(b) 120
Question
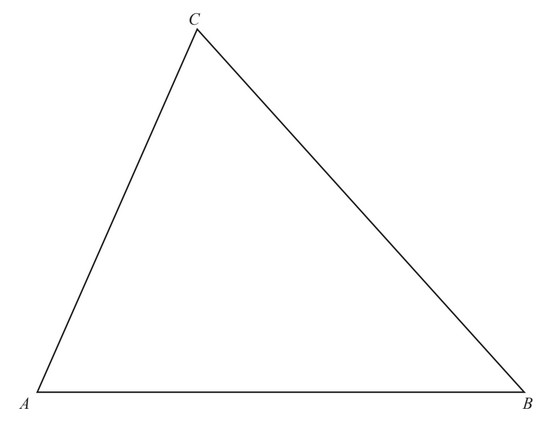
(a) Construct the locus of points, inside the triangle, that are 5cm from B.
(b) Construct the locus of points, inside the triangle, that are equidistant from AB and BC.
(c) Shade the region, inside the triangle, containing points that are
• more than 5cm from B
and
• nearer to AB than to BC.
Answer/Explanation
Ans:
(a) Accurate arc, centre B, radius 5 cm meeting both BA and BC
(b) Accurate bisector through angle B with 2 pairs of correct arcs and reaching to at least AC
(c) Correct region identified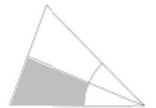
Question
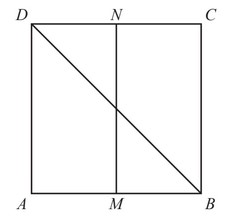
The diagram shows a square ABCD.
M is the midpoint of AB and N is the midpoint of CD.
(a) Complete the statement.
The line MN is the locus of points inside the square which are
(b) Shade the region inside the square containing points which are
nearer to AB than to BC and nearer to A than to B.
Answer/Explanation
Ans:
(a) Equidistant from A and B
(or C and D or AD and BC)
(b) 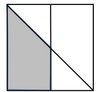
Question
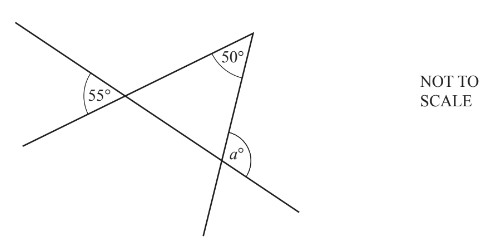
Use the information in the diagram to fi nd the value of a.
Answer/Explanation
Ans:
105
Question
A triangle has sides of length 2cm, 8cm and 9cm.
Calculate the value of the largest angle in this triangle.
Answer/Explanation
Ans: 113.9 to 114.0
Question
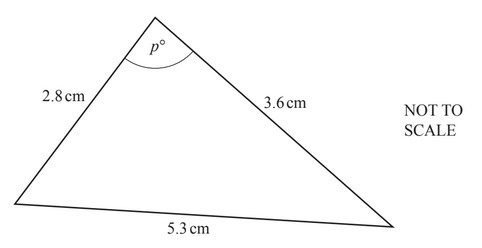
Find the value of p.
P = ………………..
Answer/Explanation
Ans:
111.2 or 111.1 to 111.2
Question
Five angles of a hexagon are each 115°.
Calculate the size of the sixth angle.
Answer/Explanation
Ans:
145
Question
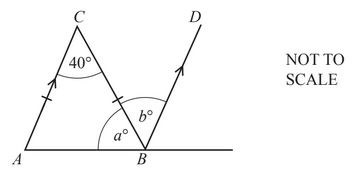
Triangle ABC is isosceles and AC is parallel to BD.
Find the value of a and the value of b.
a = …………………………………………..
b = …………………………………………..
Answer/Explanation
Ans:
[a = ] 70
[b = ] 40
Question
(a) 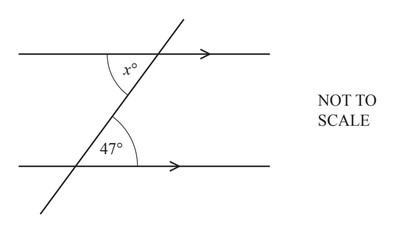
Find the value of x.
x = ………………………………………….
(b) 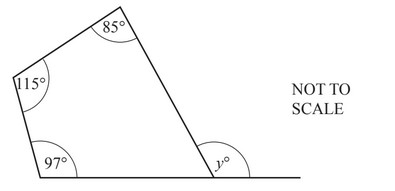
Find the value of y.
y = …………………………………………..
(c) 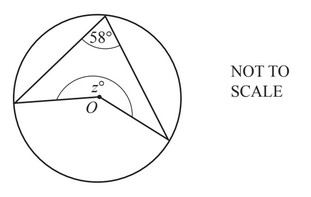
The diagram shows a circle, centre O.
Find the value of z.
z = …………………………………………..
Answer/Explanation
Ans:
(a) 47
(b) 117
(c) 244
Question
The diagram shows a regular octagon joined to an equilateral triangle.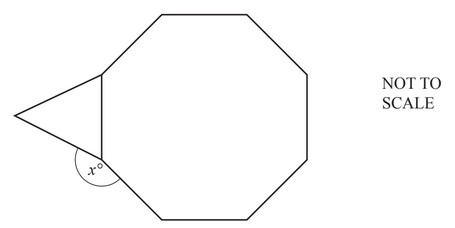
Work out the value of x.
x = …………….
Answer/Explanation
Ans:
165
Question
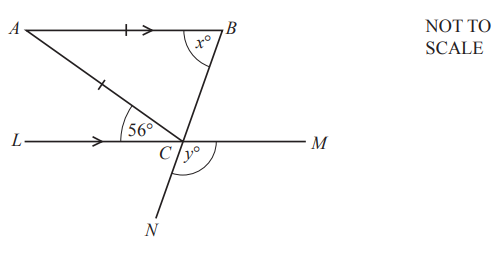
The diagram shows an isosceles triangle ABC with AB = AC.
LCM and BCN are straight lines and LCM is parallel to AB.
Angle ACL = 56°.
Find the value of x and the value of y.
Answer/Explanation
x=62
y=118
Question
(a) 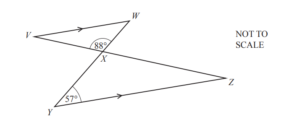
Two straight lines VZ and YW intersect at X.
VW is parallel to YZ, angle XYZ = 57° and angle VXW = 88°.
Find angle WVX.
Answer/Explanation
Ans: 35
(b) 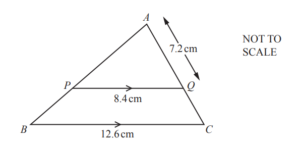
ABC is a triangle and PQ is parallel to BC.
BC = 12.6 cm, PQ = 8.4cm and AQ = 7.2 cm.
Find AC.
Answer/Explanation
Ans: 10.8
Question
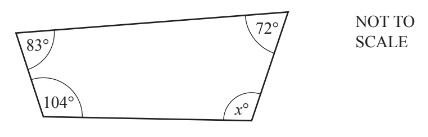
The diagram shows a quadrilateral.
Find the value of x.
x = …………………
Answer/Explanation
Ans:
101
Question
(a) 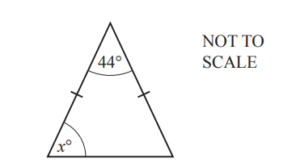
The diagram shows an isosceles triangle.
Find the value of x.
Answer/Explanation
Ans: 68
(b) The exterior angle of a regular polygon is 24°.
Find the number of sides of this regular polygon.
Answer/Explanation
Ans: 15
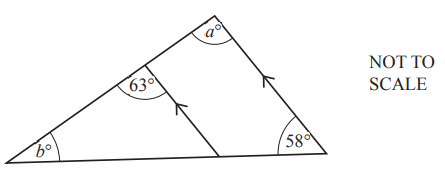
Question
Calculate angle LMN.
Angle LMN = ………………………………………..
Answer/Explanation
46.2 or 46.17 to 46.18
Question
Complete the statements.
a = ……………………………………….. because ……………………………………………………………………………………..
………………………………………………………………………………………………………………………………………………….
b = ……………………………………….. because ……………………………………………………………………………………..
………………………………………………………………………………………………………………………………………………….
Answer/Explanation
63
corresponding angles
59
angles in a trinagle add up to
180
Question
The diagram shows two parallel lines PAQ and SBCT.
AB = AC and angle QAC = 43°.
Find the value of x.
x = …………………………………
Answer/Explanation
94
Question
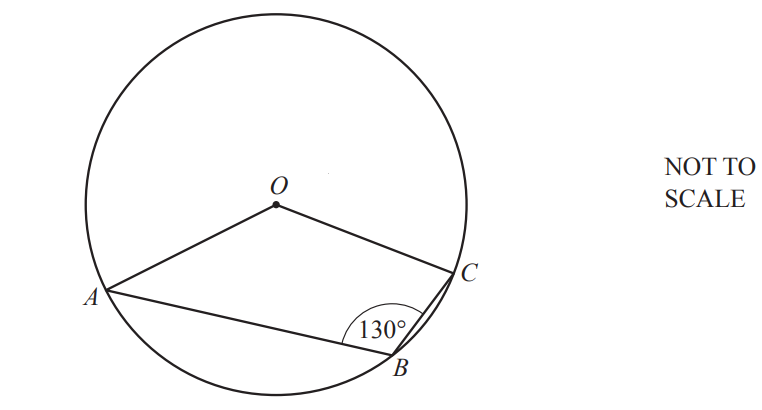
A, B and C are points on the circle, center O.
Find the obtuse angle AOC.
Angle AOC = [2]
Answer/Explanation
Ans:
8 100
Question
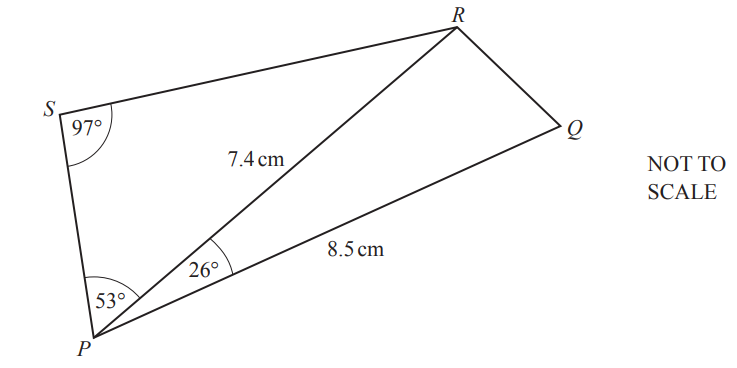
Calculate
(a) SR,
SR = __ cm [3]
(b) RQ.
RQ = __ cm [4]
Answer/Explanation
Ans:
24(a) 5.95 or 5.954…
24(b) 3.73 or 3.733 to 3.734
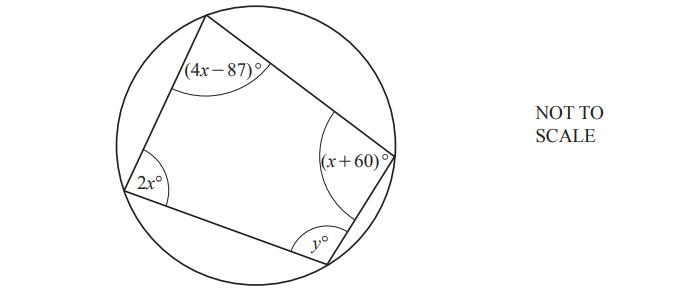
Question
The diagram shows a cyclic quadrilateral.
Find the value of y.
y = …………………………………………
Answer/Explanation
107
Question
The interior angle of a regular polygon with n sides is 156°.
Work out the value of n.
n = …………………………………………
Answer/Explanation
15
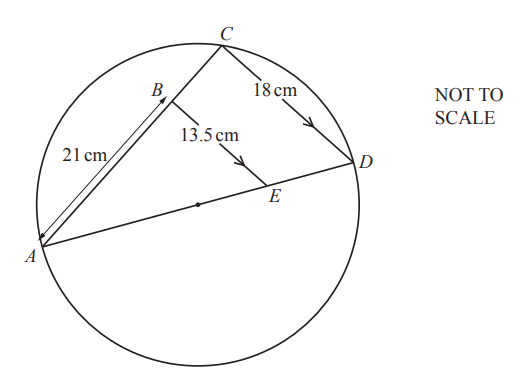
Question
C lies on a circle with diameter AD.
B lies on AC and E lies on AD such that BE is parallel to CD.
AB = 21cm, CD = 18cm and BE = 13.5cm.
Work out the radius of the circle.
Answer/Explanation
16.6 or 16.64…
Question
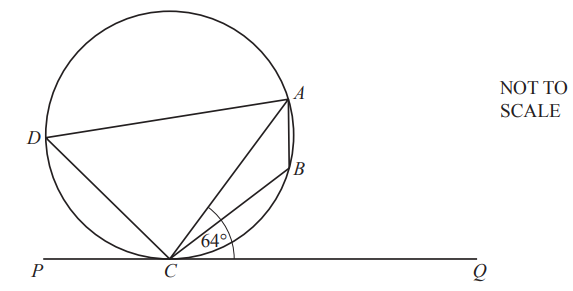
A, B, C and D lie on the circle.
PCQ is a tangent to the circle at C.
Angle ACQ = 64°.
Work out angle ABC, giving reasons for your answer.
Angle ABC = …………………….. because …………………………………………………………………………………
………………………………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………………………
Answer/Explanation
.116°
alternate segment theorem
angles in opposite segments are
supplementary or cyclic quadrilateral
or
angles at a point on a straight line
Question
The diagram shows a trapezium.
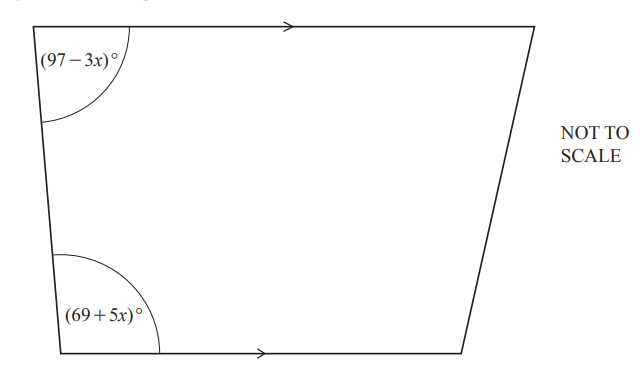
Work out the value of x.
x = …………………………………………..
Answer/Explanation
7
Question
Question
Find the interior angle of a regular polygon with 24 sides.
………………………………………….
Answer/Explanation
165
Question
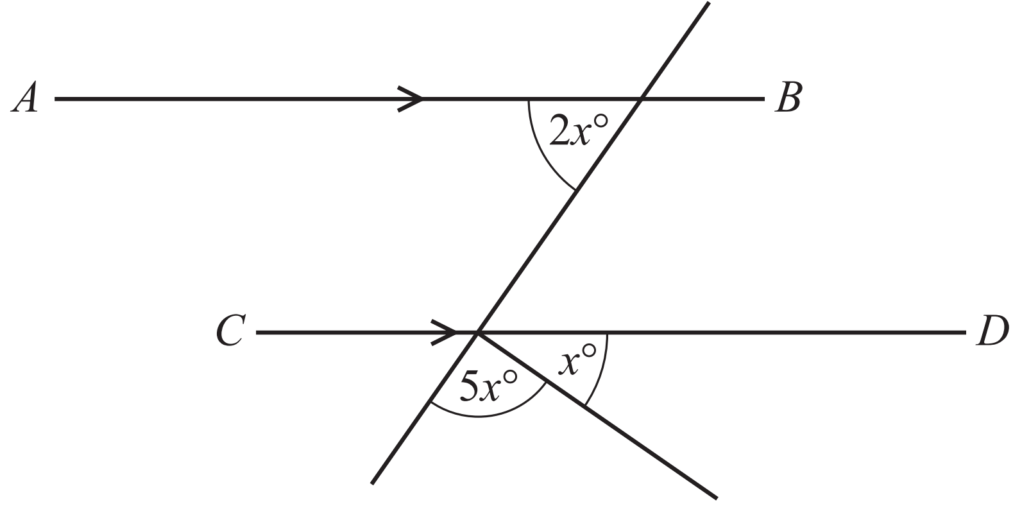
AB is parallel to CD.
Calculate the value of x.
Answer/Explanation
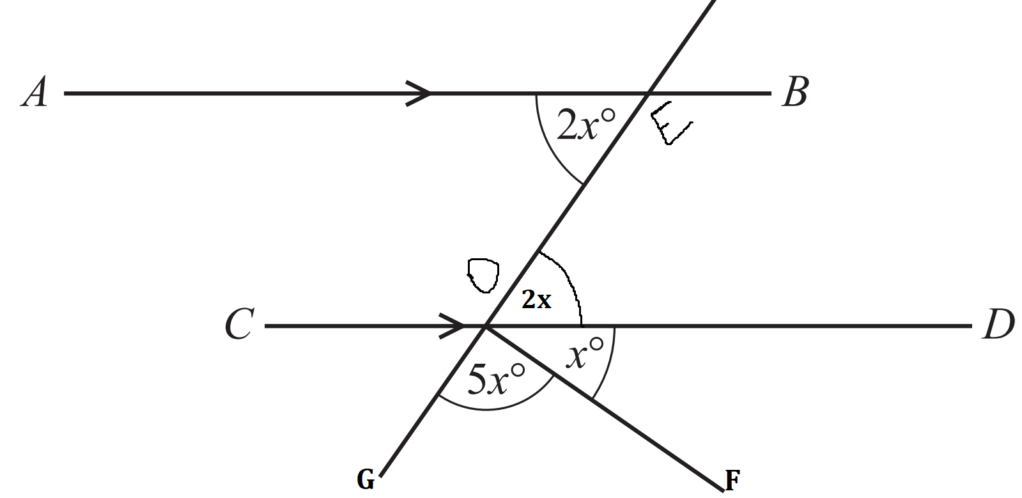
Since, AB and CD are parallel to each other,
So, \(\angle AEO\)=\(\angle DOE\) [by alternate angle property]
Now, \(\angle DOB\)+\(\angle DOF\)+\(\angle FOG\)=\(180^\circ\)
2x+x+5x=180
8x=180
x=\(22.5^\circ\)
Question
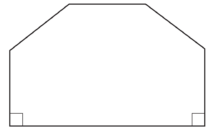
The front of a house is in the shape of a hexagon with two right angles.
The other four angles are all the same size.
Calculate the size of one of these angles.
Answer/Explanation
A hexagon consists six sides and corresponding six angles
The sum of its interior angles of a polygon is given by : \((n – 2) \times180 degrees\)
where, n is the number of sides.
For a hexagon( n = 6), sum of interior angles is:
\( (6 – 2) \times180 = 4\times 180 = 720 degrees\)
Since, two of the angles are right angles
So the sum of the other four angles is:
\( = 720 – 2 \times90 = 540 degrees\)
Since the four angles are all the same size angle,So,
\(Size of each angle = \frac{540}{4}= 135 degrees\)
Therefore, each of the four angles is 135 degrees.