Question
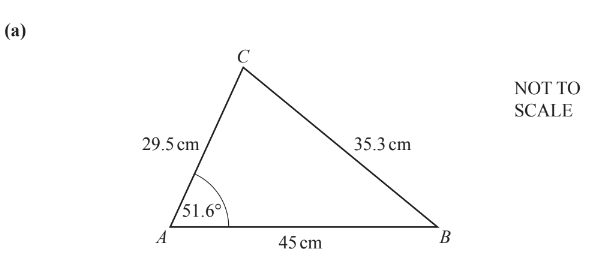
In triangle ABC, AB = 45cm, AC = 29.5cm, BC = 35.3cm and angle CAB = 51.6°.
(i) Calculate angle ABC.
(ii) Calculate the area of triangle ABC.
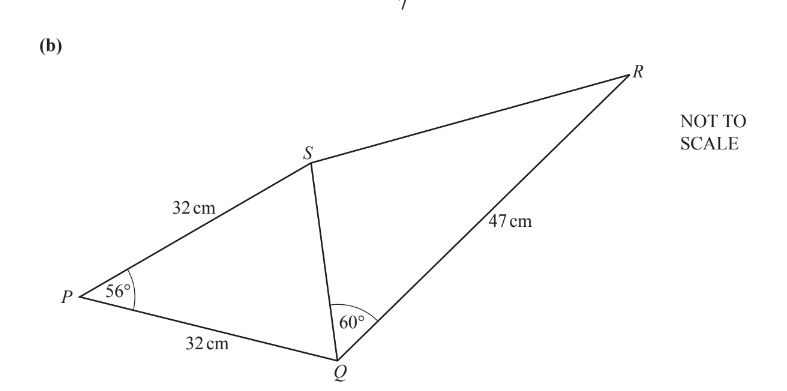
The diagram shows a quadrilateral PQRS formed from two triangles, PQS and QRS.
Triangle PQS is isosceles, with PQ = PS = 32cm and angle SPQ = 56°.
QR = 47cm and angle SQR = 60°.
(i) Calculate SR.
(ii) Calculate the shortest distance from P to SQ.
Answer/Explanation
4(a)(i) 40.9 or 40.91…
4(a)(ii) 520 or 520.0 to 520.2…
4(b)(i) 41.2 or 41.21 to 41.23
4(b)(ii) 28.3 or 28.25 to 28.29…
Question
(a) A rectangle measures 8.5cm by 10.7cm, both correct to 1 decimal place.
Calculate the upper bound of the perimeter of the rectangle.
…………………………………….. cm
(b)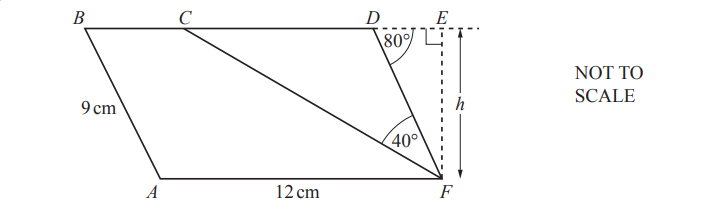
ABDF is a parallelogram and BCDE is a straight line.
AF = 12cm, AB = 9 cm, angle CFD = 40° and angle FDE = 80°.
(i) Calculate the height, h, of the parallelogram.
h = ……………………………………. cm
(ii) Explain why triangle CDF is isosceles.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(iii) Calculate the area of the trapezium ABCF.
(c)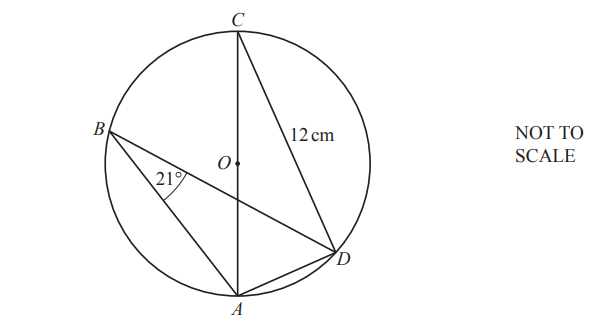
A, B, C and D are points on the circle, centre O.
Angle ABD = 21° and CD = 12 cm.
Calculate the area of the circle.
…………………………………… \(cm^{2}.\)
(d)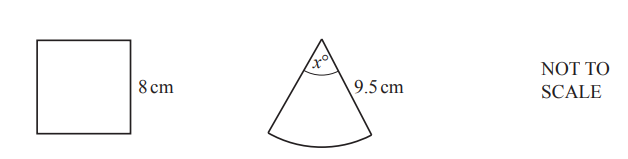
The diagram shows a square with side length 8cm and a sector of a circle with radius 9.5cm
and sector angle x°.
The perimeter of the square is equal to the perimeter of the sector.
Calculate the value of x.
x = …………………………………………
Answer/Explanation
(a) 38.6
(b)(i) 8.86 or 8.863…
(ii) ∠CDF = 100 leading to ∠DCF = 40
Or
∠EDF = 80 leading to ∠DCF = 40
two equal angles’
(iii) 66.5 or 66.45 to 66.47…
(c) 130 nfww or 129.6 to 129.8
(d) 78.4 or 78.37 to 78.41
Question
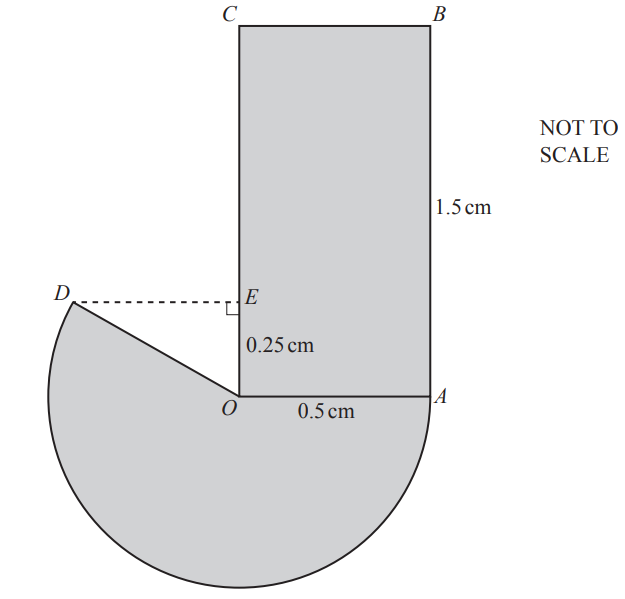
The diagram shows a company logo made from a rectangle and a major sector of a circle.
The circle has center O and radius OA.
OA = OD = 0.5cm and AB = 1.5 cm.
E is a point on OC such that OE = 0.25cm and angle OED = 90°.
(a) Calculate the perimeter of the logo.
cm [5]
(b) Calculate the area of the logo.
cm2 [3]
(c) A mathematically similar logo is drawn.
The area of this logo is 77.44cm2.
(i) Calculate the radius of the major sector in this logo.
cm [3]
(ii) A gold model is made.
This model is a prism with a cross-section of area 77.44cm2.
This gold model is 15mm thick.
One cubic centimeter of gold has a mass of 19 grams.
Calculate the mass of the gold model in kilograms.
kg [3]
Answer/Explanation
Ans:
6(a) 5.83 or 5.832 to 5.833
6(b) 1.21 or 1.208…
6(c)(i) 4[.00…]
6(c)(ii) 2.20704