Question
(a)
The diagram shows a sector OXY of a circle with centre O and radius 9.5cm.
The sector angle is 53°.
A lies on OX, B lies on OY and OA = OB.
(i) Show that the area of the sector is \(41.7cm^{2}\)
, correct to 1 decimal place.
(ii) The area of triangle OAB is \(\frac{1}{3}\) of the area of sector OXY.
Calculate OA.
OA = ……………………………………. cm
(b)
The diagram shows a sector OPQ of a circle with centre O and radius 24cm.
The sector angle is 60°.
A cone is made from this sector by joining OP to OQ.
Calculate the volume of the cone.
[The volume, V, of a cone with radius r and height h is \(V=\frac{1}{3}\pi r^{2}h\).]
………………………………….. \(cm^{3}\)
Answer/Explanation
(a)(i)\(\frac{53}{360}\times \pi \times 9.5^{2}\)
1.74 to 41.75
(ii) 5.9[0] or 5.899 to 5.903..
(b) 396 or 397 or 396.4 to 396.6
Question
The diagram shows a sector of a circle with centre O, radius 8 cm and sector angle 165°.
(a) Calculate the total perimeter of the sector.
…………………………………….. cm
(b) The surface area of a sphere is the same as the area of the sector.
Calculate the radius of the sphere.
[The surface area, A, of a sphere with radius r is \(A=4\pi r^{2}.\)]
…………………………………….. cm
(c)
A cone is made from the sector by joining OA to OB.
(i) Calculate the radius, r, of the cone.
r = ……………………………………. cm
(ii) Calculate the volume of the cone.
[The volume, V, of a cone with radius r and height h is \(V=\frac{1}{3}\pi r^{2}h \).]
…………………………………… \(cm^{3}\).
Answer/Explanation
(a) 39[.0] or 39.03 to 39.04…
(b) 2.71 or 2.708…
(c)(i) 3.67 or 3.666 to 3.667
(ii) 100 or 100.0 to 100.1… final answer
Question
(a) A rectangle measures 8.5cm by 10.7cm, both correct to 1 decimal place.
Calculate the upper bound of the perimeter of the rectangle.
…………………………………….. cm
(b)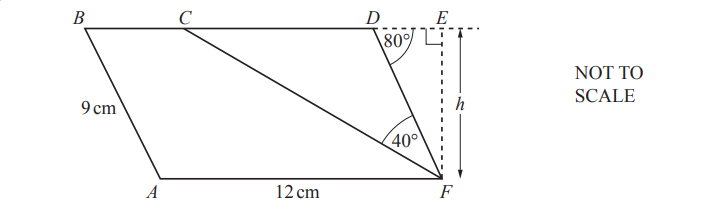
ABDF is a parallelogram and BCDE is a straight line.
AF = 12cm, AB = 9 cm, angle CFD = 40° and angle FDE = 80°.
(i) Calculate the height, h, of the parallelogram.
h = ……………………………………. cm
(ii) Explain why triangle CDF is isosceles.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(iii) Calculate the area of the trapezium ABCF.
(c)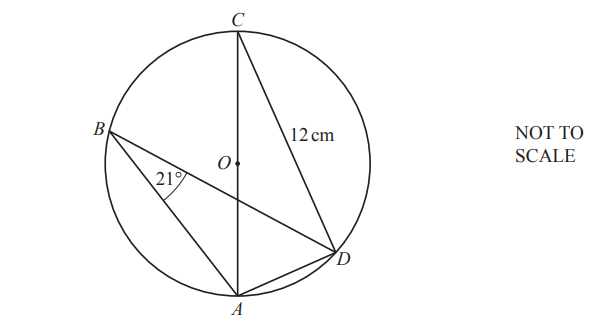
A, B, C and D are points on the circle, centre O.
Angle ABD = 21° and CD = 12 cm.
Calculate the area of the circle.
…………………………………… \(cm^{2}.\)
(d)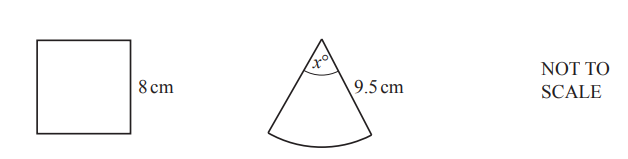
The diagram shows a square with side length 8cm and a sector of a circle with radius 9.5cm
and sector angle x°.
The perimeter of the square is equal to the perimeter of the sector.
Calculate the value of x.
x = …………………………………………
Answer/Explanation
(a) 38.6
(b)(i) 8.86 or 8.863…
(ii) ∠CDF = 100 leading to ∠DCF = 40
Or
∠EDF = 80 leading to ∠DCF = 40
two equal angles’
(iii) 66.5 or 66.45 to 66.47…
(c) 130 nfww or 129.6 to 129.8
(d) 78.4 or 78.37 to 78.41
