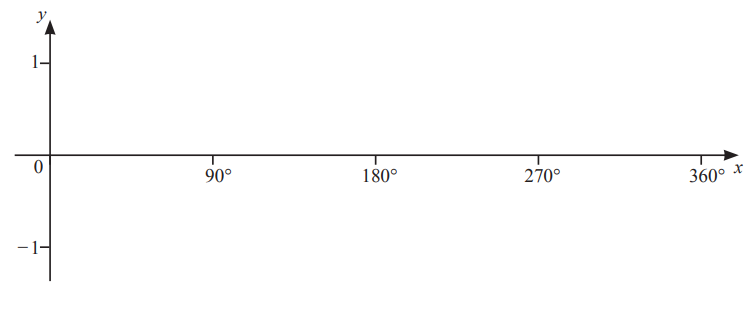
Question
(a) On the diagram, sketch the graph of \(y=\cos x\) for \(0^{\circ}\leq x\leq 360^{\circ}.\)
(b) Solve the equation \(4\cos x+2=3\) for \(0^{\circ}\leq x\leq 360^{\circ}.\)
x = ……………….. and x = ………………..
Answer/Explanation
(a)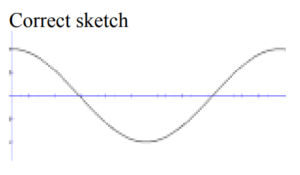
(b)75.5 or 75.52…
and
284.4 to 284.5
Question
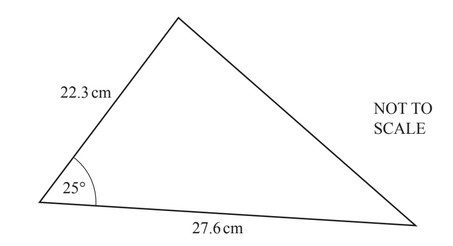
Calculate the area of this triangle.
………………………… \(\cm^2\)
Answer/Explanation
Ans:
130 or 130.0 to 130.1
Question
(a) Solve the equation tan x = 11.43 for \(0\leqslant x\leqslant 360^{\circ}\)
(b) Sketch the curve \(y=x^{3}-4x\)
(c) A curve has equation \(y=x^{3}+ax+b\)
The stationary points of the curve have coordinates (2, k) and (-2, 10 – k).
Work out the value of a, the value of b and the value of k.
Answer/Explanation
12(a) 85[.0], 265[.0] and no others
12(b) 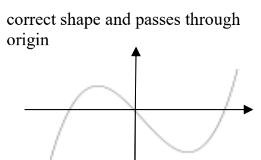
12(c) a = –12
b = 5
k = –11
Question
Write the following in order of size, largest first.
\(\sin {158}^{\circ},\cos {158}^{\circ},\cos {38}^{\circ},\sin{38}^{\circ}\)
Answer/Explanation
Since,
\(\sin{158}^{\circ}\)=0.37
\(\cos {158}^{\circ}\)=-0.92
\(\cos {38}^{\circ}\)=0.78
\(\sin{38}^{\circ}\)\=0.61
So, by the help of above values:
\(\cos {158}^{\circ}<\sin {158}^{\circ}<\sin {38}^{\circ}<\cos{38}^{\circ}\)