Question
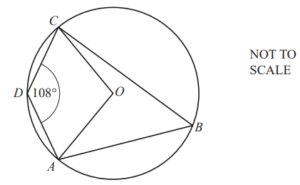
A, B, C and D lie on a circle centre O. Angle ADC = 108°.
Work out the obtuse angle AOC.
Answer/Explanation
Ans: 144
Question
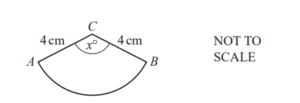
ABC is a sector of a circle, radius 4 cm and centre C.
The length of the arc AB is 8 cm and angle ACB = x°.
Calculate the value of x .
Answer/Explanation
Ans: 114.6 or 114.57 (67027..) to 114.59 (1155..)
Question
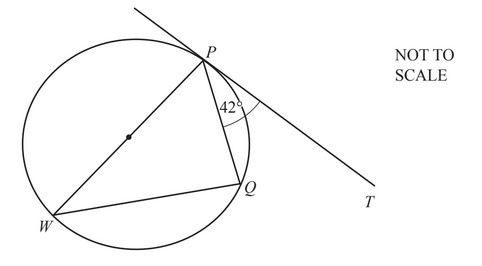
In the diagram, PT is a tangent to the circle at P.
PW is a diameter and angle TPQ = 42°.
Find angle PWQ.
Angle PWQ = …………………………………………
Answer/Explanation
Ans:
42
Question
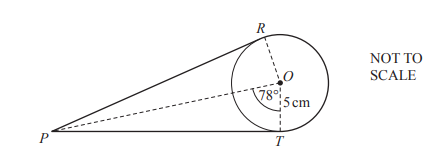
R and T are points on a circle, centre O, with radius 5 cm.
PR and PT are tangents to the circle and angle POT = 78°.
A thin rope goes from P to R, around the major arc RT and then from T to P.
Calculate the length of the rope.
Answer/Explanation
Ans: 64.8 to 64.9
Question
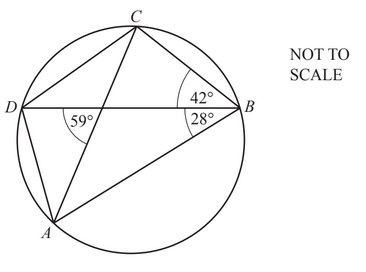
A, B, C and D lie on the circle.
Find
(a) angle ADC,
(b) angle ADB.
Answer/Explanation
Ans:
(a) Angle ADC = 110
(b) Angle ADB = 79
Question
Z E B R A
Write down the letters in the word above that have
(a) exactly one line of symmetry,
Answer/Explanation
Ans: E B A cao
(b) rotational symmetry of order 2.
Answer/Explanation
Ans: Z cao
Question
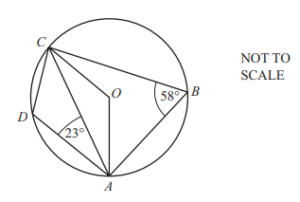
A, B, C and D lie on a circle centre O.
Angle ABC = 58° and angle CAD = 23°.
Calculate
(a) angle OCA,
Answer/Explanation
Ans: 32
(b) angle DCA.
Answer/Explanation
Ans: 35
Question
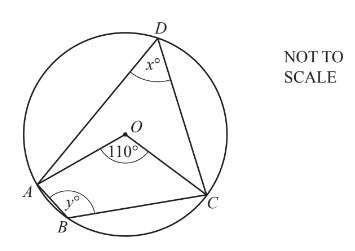
A, B, C and D lie on the circle, centre O.
Find the value of x and the value of y.
x = …………………………………………
y = …………………………………………
Answer/Explanation
Ans:
[x =] 55
[y =] 125
Question
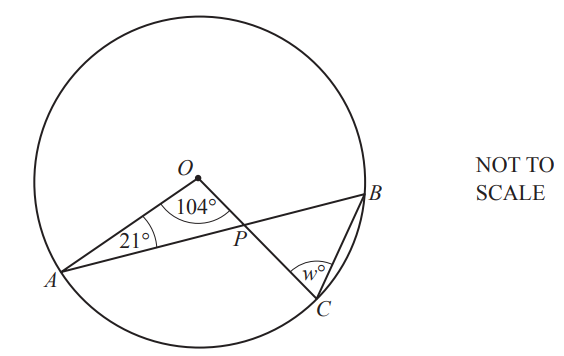
A, B and C are points on the circle, center O.
AB and OC intersect at P.
Find the value of w.
w = __
Answer/Explanation
Ans:
15 73
Question
The diagram shows a regular pentagon.
AB is a line of symmetry.
Work out the value of d.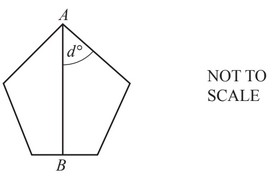
d = …………………………………………..
Answer/Explanation
Ans:
54
Question
6 Factorise completely
\(15k^{2}m-20m^{4}\)
Answer/Explanation
\(5m(3k^{2}-4m^{3})\)
Question
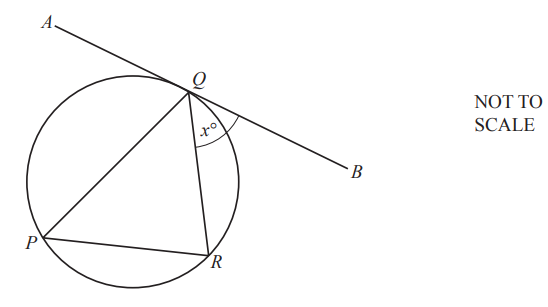
P, R and Q are points on the circle.
AB is a tangent to the circle at Q.
QR bisects angle PQB.
Angle BQR = x° and x < 60.
Use this information to show that triangle PQR is an isosceles triangle.
Give a geometrical reason for each step of your work.
Answer/Explanation
Complete explanation with
geometrical reasons
Question
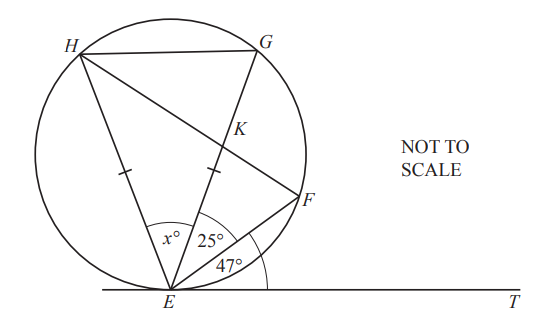
Points E, F, G and H lie on the circle and EG = EH.
HF and EG intersect at K.
ET is a tangent to the circle at E.
Angle FET = 47° and angle FEG = 25°.
Find the value of x.
Answer/Explanation
36
Question
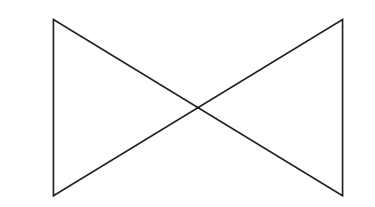
(a) Complete this statement.
The diagram has rotational symmetry of order ……………….
(b) On the diagram, draw all the lines of symmetry.
Answer/Explanation
(a) 2
(b) 2 correct lines
Question
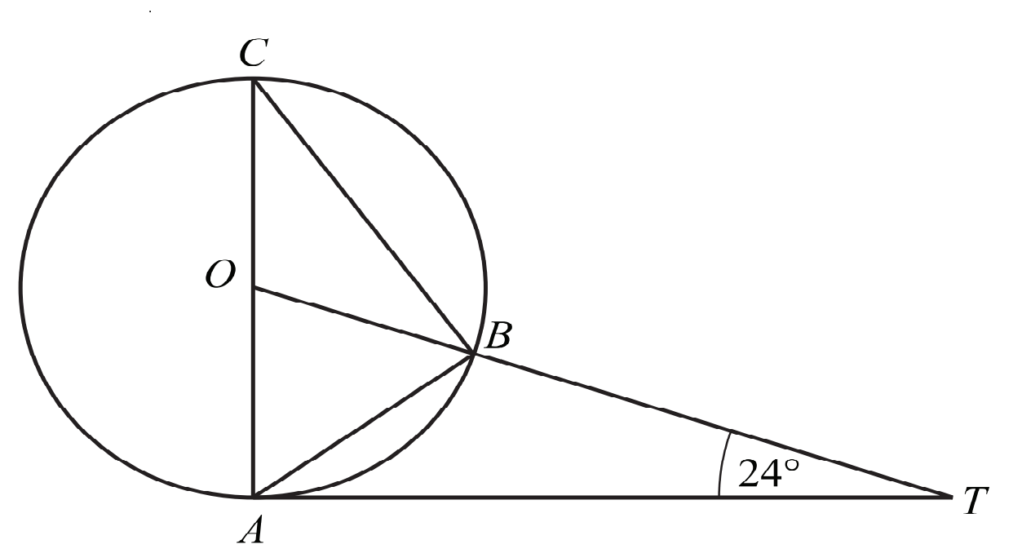
A, B and C are points on a circle, centre O.
TA is a tangent to the circle at A and OBT is a straight line.
AC is a diameter and angle OTA = 24°.
Calculate
(a) angle AOT
b) angle ACB
(c) angle ABT
Answer/Explanation
(a) Theorem: angle sum property of a triangle
sum of all interior angles of a triangle =180
Therefore, \(\angle ATO\)+\(\angle AOT\)+\(\angle OAT\)=\(180^\circ\)
Here, \(\angle OAT\)=\(90^\circ\)
Given, \(\angle ATO\)=\(24^\circ\)
24+x+90=180
x=\(66^\circ\)
(b) Here OB=OC (radius)
This implies that \(\angle OCB\)=\(\angle OBC\)(angles corresponding to equal are equal)
Let \(\angle OCB\)=\(\angle OBC\)=x
Now, TA is tangent
This implies that \(\angle AOT\)=\(90^\circ\)(tangent is perpendicular to radius at the point of contact)
In triangle AOT,
\(\angle OTA\)+\(\angle AOT\)+\(\angle OAT\)=\(180^\circ\)
90+24+\(\angle AOT\)=\(180^\circ\)
114+\(\angle AOT\)=\(180^\circ\)
\(\angle AOT\)=\(66^\circ\)
Now AC is diameter
This implies that \(\angle AOT\)+\(\angle BOC\)=\(180^\circ\)(linear pair)
\(\angle BOC\)=180-66
\(\angle BOC\)=\(114^\circ\)
Now,\(\angle BOC\)+\(\angle OCB\)+\(\angle OBC\)=\(180^\circ\)
114+2x=180
x=33
\(\angle ACB\)=\(33^\circ\)
(c) In triangle AOB , AO=BO(radius)
\(\angle ABO\)=\(\angle BAO\)(angle corresponding to equal sides are equal)
Let \(\angle ABO\)=\(\angle BAO\)=y
\(\angle AOB\)+\(\angle OBA\)+\(\angle OAB\)=\(180^\circ\)(angle sum property of triangle )
66+2y=180
y=57
In triangle ABT ,
\(\angle AOB\)+\(\angle TAB\)=\(90^\circ\)
\(\angle TAB\)=90-54
\(\angle TAB\)=33
\(\angle ABT\)+\(\angle BAT\)\(\angle ATB\)=\(180^\circ\)
\(\angle ABT\)=\(123^\circ\)
Question
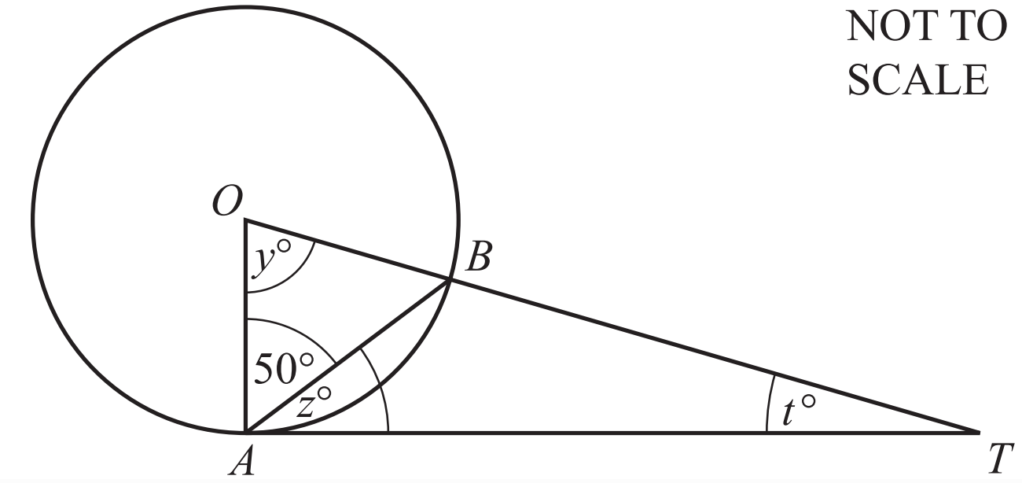
TA is a tangent at A to the circle, centre O.
Angle OAB = 50°.
Find the value of
(i) y,
(ii) z,
(iii) t
Answer/Explanation
y+50+z+t=180–(i)
In triangle AOB
y+50+\angle{ABO}=180\)
\(\angle{OAT}=90 degrees\)(As TA is tangent , at point of tangency, it is perpendicular to the radius)
So, 50+z=90 degrees
\(\Rightarrow z=40 degrees\)
Since, OA=OB, This implies, \(\angle{OAB}=\angle{OBA}\)
So, y+50+50=180
y=80 degrees
From equation(i) :
80+50+40+t=180 degrees
t=10 degrees
Question
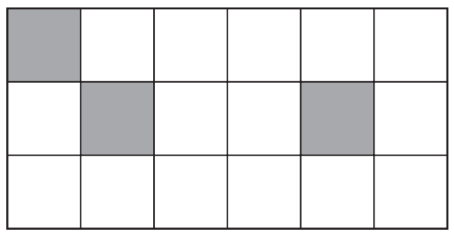
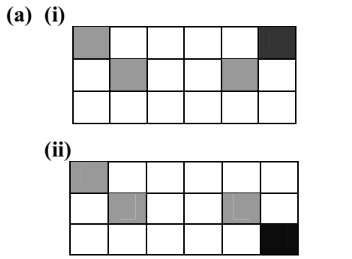
(a) Shade one square in each diagram so that there is
(i) one line of symmetry,
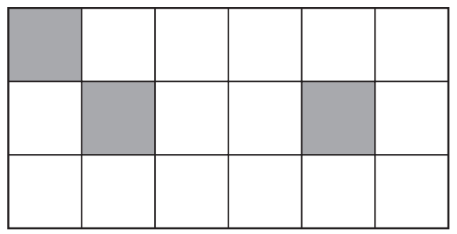
(ii) rotational symmetry of order 2.
(b) The pyramid below has a rectangular base. The vertex of the pyramid is vertically above the centre of the base. Write down the number of planes of symmetry for the pyramid.
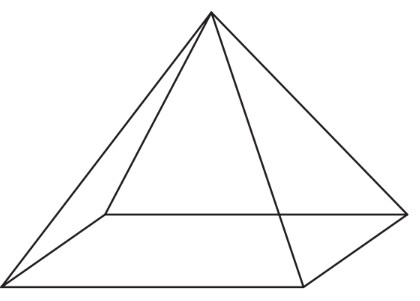
▶️Answer/Explanation
(b) 2
Question
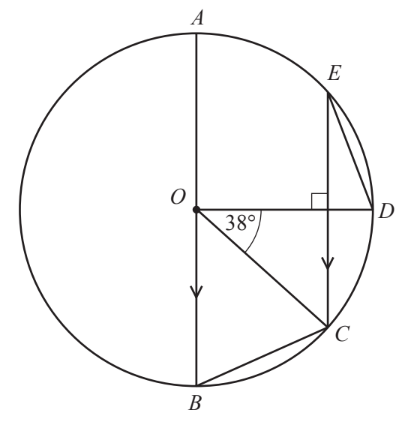
AB is the diameter of a circle, centre O. C, D and E lie on the circle. EC is parallel to AB and perpendicular to OD. Angle DOC is 38°.
Work out
(a) angle $B O C$,
(b) angle $C B O$,
(c) angle $E D O$.
▶️Answer/Explanation
(a) 52
(b) 64
(c) 71
Question
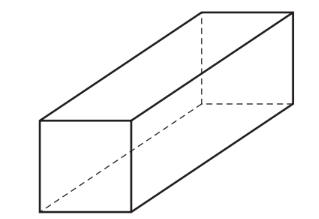
This cuboid has a square cross-section. Write down the number of planes of symmetry.
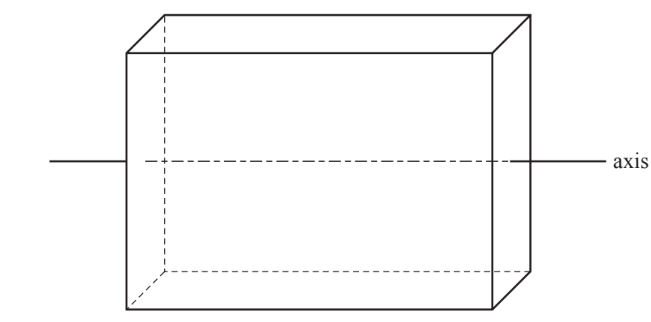
This cuboid has a rectangular cross-section.
The axis shown passes through the centre of two opposite faces.
Write down the order of rotational symmetry of the cuboid about this axis.
▶️Answer/Explanation
(a) 5
(b) 2
Question
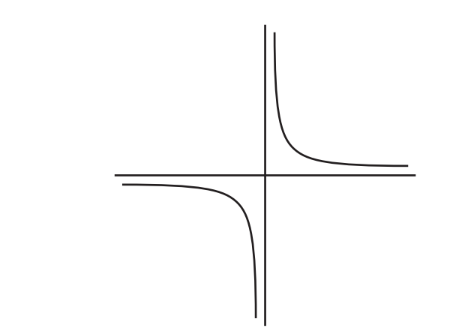
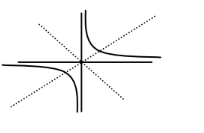
(a) Write down the order of rotational symmetry of the diagram.
(b) Draw all the lines of symmetry on the diagram.
▶️Answer/Explanation
(a) 2
(b)
Question
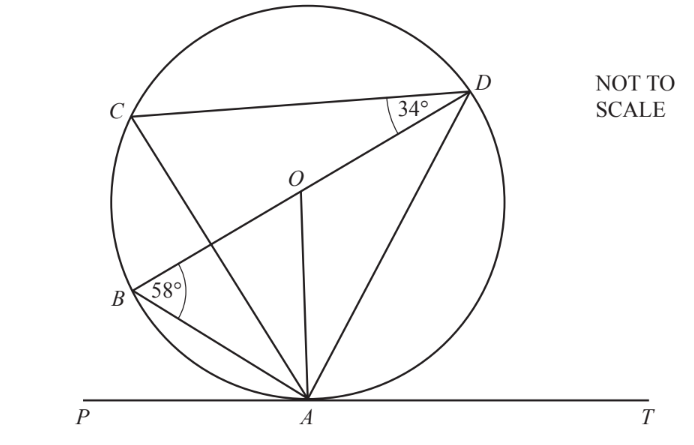
$A, B, C$ and $D$ lie on the circle, centre $O$. $B D$ is a diameter and $P A T$ is the tangent at $A$. Angle $A B D=58^{\circ}$ and angle $C D B=34^{\circ}$.
Find
(a) angle $A C D$,
(b) angle $A D B$,
(c) angle $D A T$,
(d) angle $C A O$.
▶️Answer/Explanation
(a) 58
(b) 32
(c) 58
(d) 24
Question

For the diagram above write down
(a) the order of rotational symmetry,
(b) the number of lines of symmetry.
▶️Answer/Explanation
(a) 6
(b) 0
Question
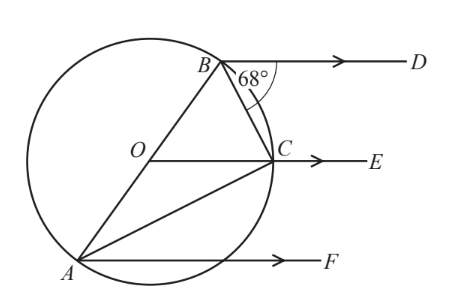
Points $A, B$ and $C$ lie on a circle, centre $O$, with diameter $A B$. $B D, O C E$ and $A F$ are parallel lines.
Angle $C B D=68^{\circ}$.
Calculate
(a) angle $B O C$,
(b) angle ACE.
▶️Answer/Explanation
(a) 44
(b) 158