Question
(a) Find the magnitude of the vector \(\binom{-1}{7}\).
(b) The determinant of the matrix \(\begin{pmatrix}6 &2m \\ 5 & m\end{pmatrix}\)Find the value of m
(c) \(L=\begin{pmatrix}2 &5 \\ 3 & 9\end{pmatrix}\) \(M= \binom{-4}{2}\) N=(\(1\) \(7)\)
Work out the following.
(i) NM
…………………………………………
(ii) LM
………………………………………..
(iii) \(L^{2}\)
…………………………………………
(iv) \(L^{-1}\)
…………………………………………
Answer/Explanation
(a) 7.07 or 7.071…
(b)−6
(c)(i) (10) final answer
(ii)\(\binom{2}{6}\) final answer
(iii)\(\begin{pmatrix}19 & 55\\ 33 & 96\end{pmatrix}\) final answer
(iv)\( \frac{1}{3}\begin{pmatrix}9 & -5 \\ -3 & 2\end{pmatrix}\)
Question
(a) \(\vec{OA}=\begin{pmatrix}4\\ 3\end{pmatrix} \) \(\vec{AB}=\begin{pmatrix}8\\ -7\end{pmatrix} \) \(\vec{AC}=\begin{pmatrix}-3\\ 6\end{pmatrix}\)
Find
(i)\(\left | \vec{OB} \right |,\)
\(\left | \vec{OB} \right |=……………………….\)
(ii)\( \left | \vec{BC} \right |,\)
\(\left | \vec{BC} \right |…………………..\)
(b)
PQRS is a parallelogram with diagonals PR and SQ intersecting at X.
\(\vec{PQ}= a\) and \(\vec{PS}=b.\)
Find \vec{QX} in terms of a and b.
Give your answer in its simplest form.
\(\vec{QX} = ………………………………………..\)
(c)\( M=\begin{pmatrix}2 & 5 \\ 1 & 8\end{pmatrix}\)
Calculate
(i)\( M^{2},\)
\(M^{2}=\left ( \right )\)
(ii)\(M^{-1}\)
\(M^{-1}=\left ( \right )\)
Answer/Explanation
(a)(i) 12.6 or 12.64 to 12.65
(ii) \(\begin{pmatrix}-11\\ 13\end{pmatrix}\)
(b)\(\frac{1}{2}(b-a)\)
(c)(i) \(\begin{pmatrix}9 & -50\\ 10 & 69\end{pmatrix}\)
(ii)\(\frac{1}{11}\begin{pmatrix}8 & -5\\ -1 & 2\end{pmatrix}\)
Question
(a) 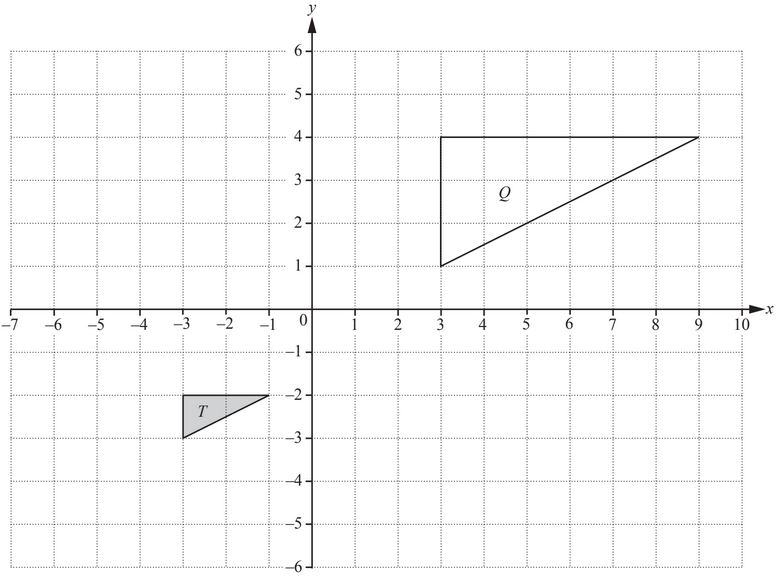
(i) Draw the image of triangle T after a translation by the vector \(\begin{pmatrix}
5\\-2
\end{pmatrix}\)
(ii) Draw the image of triangle T after a reflection in the line y = 1.
(iii) Describe fully the single transformation that maps triangle T onto triangle Q.
(b) M = \(\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}\) N = \(\begin{pmatrix}
4 & 3\\
1 & k
\end{pmatrix}\) P = \(\begin{pmatrix}
1 & 3\\
0 & 6
\end{pmatrix}\)
(i) Work out M +P.
(ii) Work out PM.
(iii) |M| = |N|
Find the value of k.
k = ……………………………..
(c) (i) Describe fully the single transformation represented by the matrix \(\begin{pmatrix}
0 & -1\\
1 & 0
\end{pmatrix}\)
(ii) Find the matrix which represents a reflection in the line y = x.
Answer/Explanation
Answer:
(a) (i) Triangle drawn,
vertices (2, – 4), (2, – 5), (4, – 4)
(ii) Triangle drawn,
vertices (– 3, 4), (– 3, 5), (– 1, 4)
(iii) Enlargement
[factor] 3
[centre] (– 6, – 5)
(b) (i) \(\begin{pmatrix}
2 & 5\\
3 & 10
\end{pmatrix}\)
(ii) \(\begin{pmatrix}
10 & 14\\
18 & 24
\end{pmatrix}\) final answer
(iii) \(\frac{1}{4}\) oe
(c) (i) Rotation
90 ̊ [anti-clockwise] oe
(0, 0) oe
(ii) \(\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}\)