Question
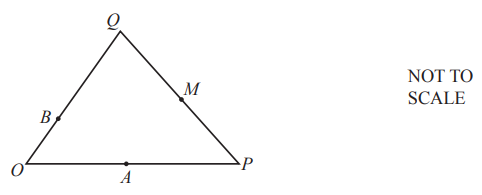
O is the origin, \(\underset{OP}{\rightarrow}=\underset{2OA}{\rightarrow},\underset{OQ}{\rightarrow}=\underset{3OB}{\rightarrow} and \underset{PM}{\rightarrow}=\underset{MQ}{\rightarrow}.\)
\(\underset{OP}{\rightarrow}=p\) and \(\underset{OQ}{\rightarrow}=q\).
Find, in terms of p and q, in its simplest form
(a) \(\underset{BA}{\rightarrow}\),
\(\underset{BA}{\rightarrow}\) = [2]
(b) the position vector of M.[2]
Answer/Explanation
Ans:
25(a) \(-\frac{1}{3}q+\frac{1}{2}p\) oe
25(b) \(\frac{1}{2}p+\frac{1}{2}q\) oe
Question
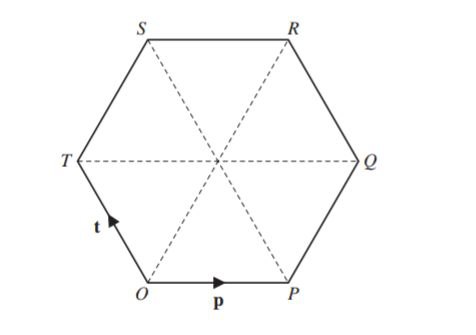
O is the origin and OPQRST is a regular hexagon.
\(\overrightarrow{OP}=p and \overrightarrow{OT}=t.\)
Find, in terms of p and t, in their simplest forms,
(a) \(\overrightarrow{PT}\),
Answer/Explanation
Ans: -p+t
(b) \(\overrightarrow{PR}\),
Answer/Explanation
Ans: p+2t
(c) the position vector of R.
Answer/Explanation
Ans: 2(p + t) or 2p + 2t
Question
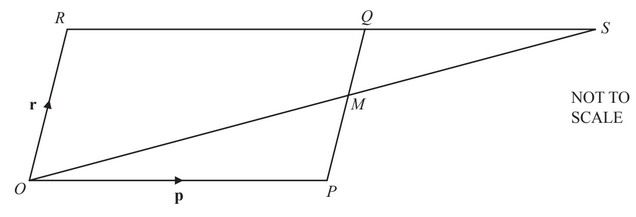
OPQR is a parallelogram, with O the origin.
M is the midpoint of PQ.
OM and RQ are extended to meet at S.
\(\overrightarrow{OP}=p\) and \(\overrightarrow{OR}=r\).
(a) Find, in terms of p and r, in its simplest form,
(i) \(\overrightarrow{OM}\),
(ii) the position vector of S.
(b) When \(\overrightarrow{PT} = -\frac{1}{2}p + r\), what can you write down about the position of T?
Answer/Explanation
Ans:
(a) (i) \(\overrightarrow{OM} = p + \frac{1}{2} r\)
(ii) 2p + r
(b) Midpoint of RQ
Question
\(M=\bigl(\begin{smallmatrix}1 & & 2\\3 & & 4\end{smallmatrix}\bigr)\) \(P=\bigl(\begin{smallmatrix}5 & & 6\\7 & & 8\end{smallmatrix}\bigr)\)
(a) Find MP.
\(\begin{pmatrix}& & \\& &\end{pmatrix}\)[2]
(b) Find \(\left | M \right |\) .[1]
Answer/Explanation
Ans:
19(a) \(\begin{pmatrix}19 & 22\\43 & 50\end{pmatrix}\)
19(b) –2 final answer
Question
O is the origin, \(\underset{OA}{\rightarrow} = 2x+3y\) and \(\underset{BA}{\rightarrow} = x-4y.)
Find the position vector of B, in terms of x and y, in its simplest form.[2]
Answer/Explanation
Ans:
8 x + 7y
Question
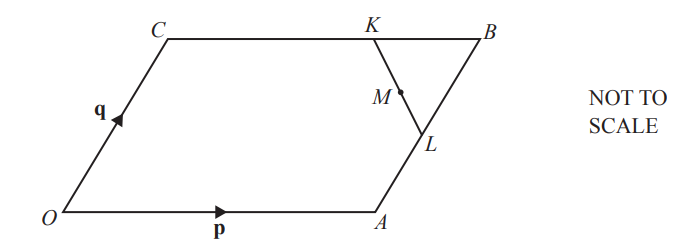
OABC is a parallelogram and O is the origin.
CK = 2KB and AL = LB.
M is the midpoint of KL.
\(\underset{OA}{\rightarrow}\) = p and \(\underset{OC}{\rightarrow}\)= q.
Find, in terms of p and q, giving your answer in its simplest form
(a) \(\underset{KL}{\rightarrow}\),
\(\underset{KL}{\rightarrow}\) = [2]
(b) the position vector of M. [2]
Answer/Explanation
Ans:
25(a) \(\frac{1}{3}p-\frac{1}{2}q\) oe simplified
25(b) \(\frac{5}{6}p-\frac{3}{4}q\) oe simplified
Question
(a) Ahmed increases 40 by 300%.
From this list, put a ring around the correct calculation.
\(40\times 1.300\) \( 40\times 3 \) \(40\times400\) \(40\times 40\) \( 40\times 4\) \(40\times 300\)
(b) Ahmed finds the magnitude of the vector\(\begin{pmatrix}2\\ -3\end{pmatrix}.\)
From this list, put a ring around the correct calculation.
\(\sqrt{2^{2}+-3^{2}}\) \(2^{2} -3^{2}\) \( \sqrt{2^{2}-3^{2}}\) \(2^{2}+(-3)^{2}\) \( \sqrt{2^{2}+(-3)^{2}}\).
Answer/Explanation
(a) 40 × 4
(b) \(\sqrt{2^{2}+(-3)^{2}}\)
Question
\(\vec{XY}=3a+2b\) and \(\vec{ZY}=6a+4b\)
Write down two statements about the relationship between the points X, Y and Z.
1 ……………………………………………………………………………………………………………………………………….
2 ……………………………………………………………………………………………………………………………………….
Answer/Explanation
X,YandZ are collinear
X is the midpoint of ZY
Question
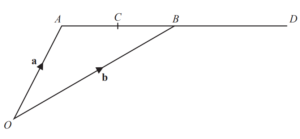
A and B have position vectors a and b relative to the origin O.
C is the midpoint of AB and B is the midpoint of AD.
Find, in terms of a and b, in their simplest form
(a) the position vector of C
(b) the vector CD
Answer/Explanation
(a) \(\frac{1}{2} a +\frac{1}{2} b \)
(b) \(\frac{-1}{2}+\frac{3}{2}\)
Question
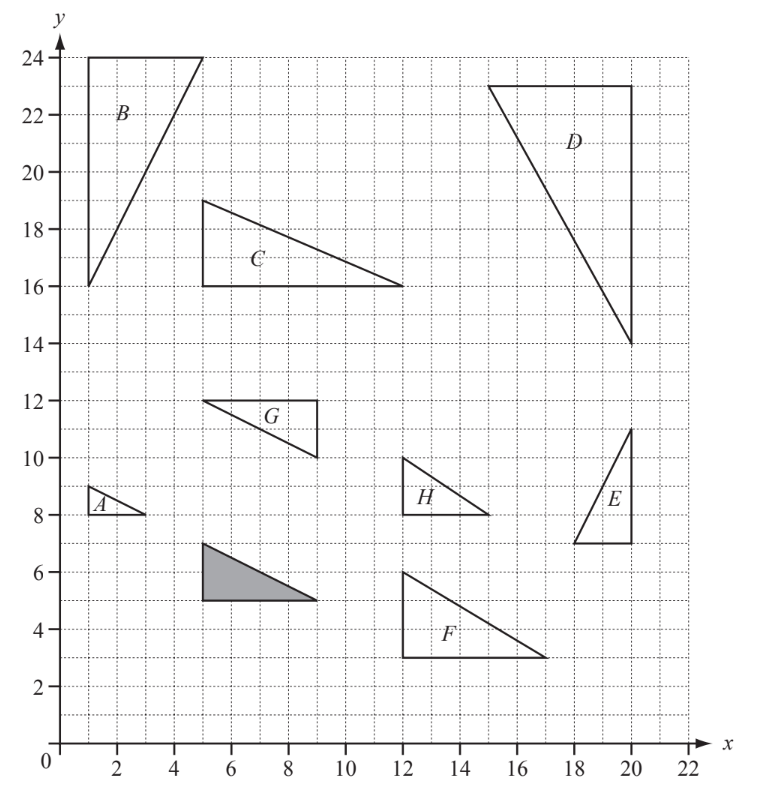
Write down the letters of all the triangles which are
(a) congruent to the shaded triangle,
(b) similar, but not congruent, to the shaded triangle.
▶️Answer/Explanation
(a) E, G
(b) A, B
Question
(a) A is a (2 × 4) matrix, B is a (3 × 2) matrix and C is a (1 × 3) matrix. Which two of the following matrix products is it possible to work out?
$\begin{array}{lll}\mathbf{A}^2 \quad \mathbf{B}^2 \quad \mathbf{C}^2\end{array}$ AB AC BA BC CA CB
(b) Find the inverse of
$
\left(\begin{array}{cc}
\frac{1}{2} & \frac{3}{4} \\
\frac{1}{8} & \frac{1}{4}
\end{array}\right)
$
Simplify your answer as far as possible.
(c) Explain why the matrix $\left(\begin{array}{ll}4 & 2 \\ 6 & 3\end{array}\right)$ does not have an inverse.
▶️Answer/Explanation
(a) $\mathbf{C B}$ and $\mathbf{B A}$ cao
(b) $\left(\begin{array}{cc}8 & -24 \\ -4 & 16\end{array}\right)$ cao
(c) determinant is zero
Question
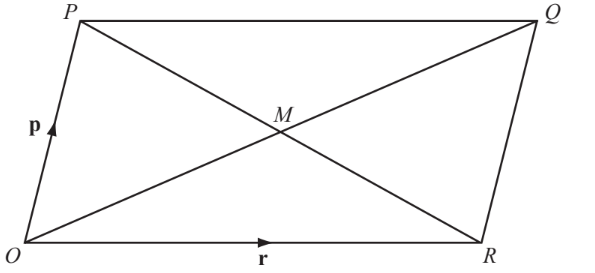
$O$ is the origin and $O P Q R$ is a parallelogram whose diagonals intersect at $M$.
The vector $\overrightarrow{O P}$ is represented by $\mathbf{p}$ and the vector $\overrightarrow{O R}$ is represented by $\mathbf{r}$.
(a) Write down a single vector which is represented by
(i) $\mathbf{p}+\mathbf{r}$,
(ii) $\frac{1}{2} \mathbf{p}-\frac{1}{2} \mathbf{r}$.
(b) On the diagram, mark with a cross $(\mathrm{x})$ and label with the letter $S$ the point with position vector
$
\frac{1}{2} \mathbf{p}+\frac{3}{4} \mathbf{r} \text {. }
$
▶️Answer/Explanation
(a) (i) OQ
(ii) RM or MP
(b)