Question
This year, 40 students have each travelled by one or more of plane (P), train (T) or boat (B).
7 have travelled only by plane.
11 have travelled only by train.
9 have travelled only by boat.
\(n(P\cap T) = 8\)
\(n(B\cap T )= 3\)
\(n(B\cap P )= 6\)

(A) Complete the Venn diagram.
(b) Find \(n((P\cup B){}’)\)
………………………………………….
(c) Use set notation to complete the statement.
\(\left ( P \cup T\cup B\right ){}’= ………………………\)
(d) Two students are chosen at random.
Calculate the probability that they both have travelled only by plane.
………………………………………….
(e) Two students are chosen at random from those who have travelled by train.
Calculate the probability that they both have also travelled by plane.
………………………………………….
Answer/Explanation
(a)
(b) 11
(c)\(\phi\) or {}
(d)\(\frac{7}{260}\)
(e)\(\frac{14}{95}\)
Question
(a) The probability that Shalini is late for school on any day is\( \frac{1}{6}\)
(i) Complete the tree diagram for Monday and Tuesday.
Monday Tuesday
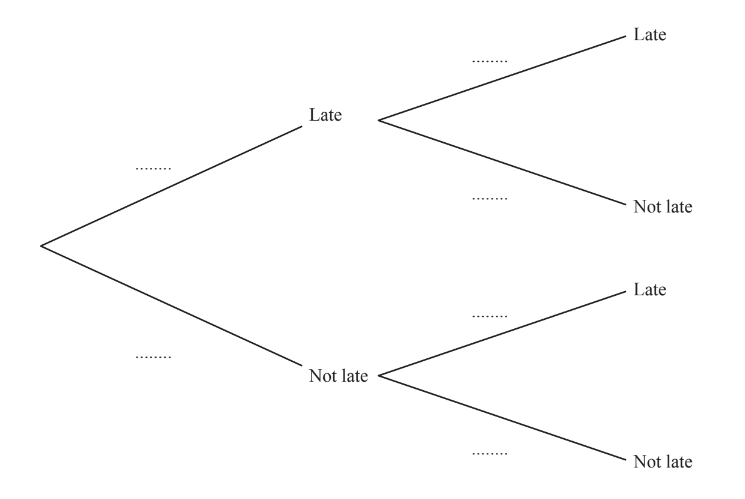
(ii) Calculate the probability that Shalini is late on Monday but is not late on Tuesday.
(b) The Venn diagram shows the number of students in a group of 50 students who wear glasses (G), who wear trainers (T ) and who have a mobile phone (M ).
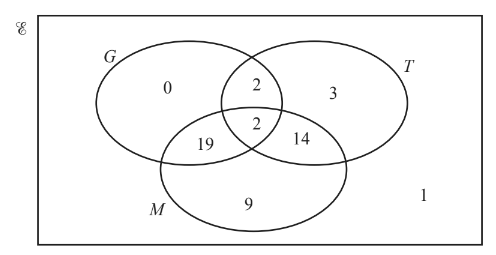
(i) Use set notation to describe the region that contains only one student.
(ii) Find n\( \left ( T’\cap (G\cup M) \right )\)
(iii) One student is picked at random from the 50 students.
Find the probability that this student wears trainers but does not wear glasses.
(iv) Two students are picked at random from those wearing trainers.
Find the probability that both students have mobile phones
Answer/Explanation
.
11(a)(i)\( \frac{1}{6}\) oe on all late branches
11(a)(i) \( \frac{5}{6}\) oe on all late branches
11(a)(ii) \(\frac{5}{36}oe\)
11(b)(i) \( (G\cup T\cup M)’\)oe
11(b)(ii) 28
11(b)(iii) \(\frac{17} {50}oe
11(b)(iv) \(\frac{4}{7}\) oe
Question
(a) There are 32 students in a class.
5 do not study any languages.
15 study German (G).
18 study Spanish (S).
(i) Complete the Venn diagram to show this information.
(ii) A student is chosen at random.
Find the probability that the student studies Spanish but not German.
………………………………………….
(iii) A student who studies German is chosen at random.
Find the probability that this student also studies Spanish.
………………………………………….
(b) A bag contains 54 red marbles and some blue marbles.
36% of the marbles in the bag are red.
Find the number of blue marbles in the bag.
………………………………………….
(c) Another bag contains 15 red beads and 10 yellow beads.
Ariana picks a bead at random, records its colour and replaces it in the bag.
She then picks another bead at random.
(i) Find the probability that she picks two red beads.
………………………………………….
(ii) Find the probability that she does not pick two red beads.
………………………………………….
(d) A box contains 15 red pencils, 8 yellow pencils and 2 green pencils.
Two pencils are picked at random without replacement.
Find the probability that at least one pencil is red.
………………………………………….
Answer/Explanation
(a)(i)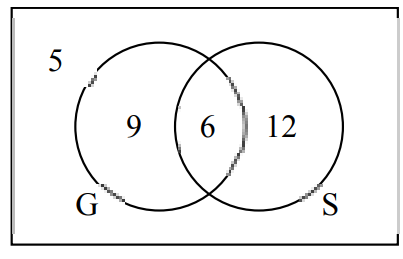
(ii)\(\frac{3}{8}\)
(iii)\(\frac{2}{5}\)
(b) 96
(c)(i) \(\frac{9}{25}\)
(ii)\( \frac{16}{25}\)
(d)\(\frac{17}{20}\)
Question
Sushila, Ravi and Talika each have a bag of balls.
Each of the bags contains 10 red balls and 8 blue balls.
(a) Sushila takes one ball at random from her bag.
Find the probability that she takes a red ball.[1]
(b) Ravi takes two balls at random from his bag, without replacement.
Find the probability that one ball is red and one ball is blue. [3]
(c) Talika takes three balls at random from her bag, without replacement.
Calculate the probability that the three balls are the same colour.[4]
Answer/Explanation
Ans:
3(a) \(\frac{5}{9} oe\)
3(b) \(\frac{80}{153} oe\)
3(c) \(\frac{11}{51} oe\)
Question
(a) A bag contains red beads and green beads.
There are 80 beads altogether.
The probability that a bead chosen at random is green is 0.35 .
(i) Find the number of red beads in the bag.
(ii) Marcos chooses a bead at random and replaces it in the bag.
He does this 240 times.
Find the number of times he would expect to choose a green bead.
(b) A different bag contains 2 blue marbles, 3 yellow marbles and 4 white marbles.
Huma chooses a marble at random, notes the colour, then replaces it in the bag.
She does this three times.
Find the probability that
(i) all three marbles are yellow,
(ii) all three marbles are different colours.
(c) Another bag contains 2 green counters and 3 pink counters.
Teresa chooses three counters at random without replacement.
Find the probability that she chooses more pink counters than green counters.
Answer/Explanation
Ans:
(a) (i) 52
(ii) 84
(b) (i) \(\frac{27}{729}\) oe
(ii) \(\frac{144}{729}\) oe
(c) \(\frac{42}{60}\) oe
Question
(a) 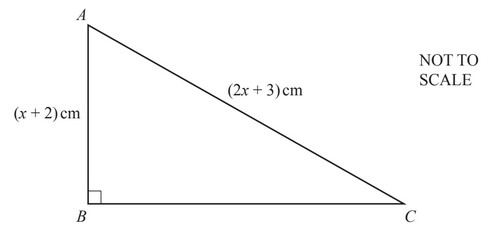
In triangle ABC, AB = (x + 2) cm and AC = (2x + 3) cm.
sin ACB = \(\frac{9}{16}\)
Find the length of BC.
(b) A bag contains 7 white beads and 5 red beads.
(i) The mass of a red bead is 2.5 grams more than the mass of a white bead.
The total mass of all the 12 beads is 114.5 grams.
Find the mass of a white bead and the mass of a red bead.
(ii) Two beads are taken out of the bag at random, without replacement.
Find the probability that
(a) they are both white,
(b) one is white and one is red.
Answer/Explanation
Answer:
(a) 6.61 (6.614…) www
(b) (i) White = 8.5, red = 11
(ii) (a) \(\frac{42}{132}\) or \(\frac{21}{66}\) oe \(\frac{14}{44}\) oe \(\frac{7}{22}\)
(ii) (b) \(\frac{70}{132}\) or \(\frac{35}{66}\)
(0.53[0] or 0.5303…)
Question
90 students are asked which school clubs they attend.
D = {students who attend drama club}
M = {students who attend music club}
S = { students who attend sports club}
39 students attend music club.
26 students attend exactly two clubs.
35 students attend drama club.
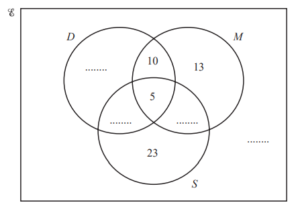
(a) Write the four missing values in the Venn diagram.
Answer/Explanation
Ans: 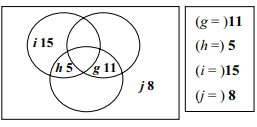
(b) How many students attend
(i) all three clubs,
Answer/Explanation
Ans: 5
(ii) one club only?
Answer/Explanation
Ans: 51
(c) Find
(i) n(D ∩ M),
Answer/Explanation
Ans: 15
(ii) n((D ∩ M) ∩ S’ ).
Answer/Explanation
Ans: 10
(d) One of the 90 students is chosen at random.
Find the probability that the student
(i) only attends music club,
Answer/Explanation
Ans: \(\frac{13}{90}oe[0.144]\)
(ii) attends both music and drama clubs.
Answer/Explanation
Ans: \(\frac{15}{90}oe[0.167]\)
(e) Two of the 90 students are chosen at random without replacement.
Find the probability that
(i) they both attend all three clubs,
Answer/Explanation
Ans: \(\frac{20}{8010}oe[0.0025[0]]\)
(ii) one of them attends sports club only and the other attends music club only.
Answer/Explanation
Ans: \(\frac{598}{8010}oe[0.0747]\)
Question
The probability that it rains on Monday \(\frac{3}{5}\)
If it rains on Monday, the probability that it rains on Tuesday is \(\frac{4}{7}\)
If it does not rain on Monday, the probability that it rains on Tuesday is \(\frac{5}{7}\)
(a) Complete the tree diagram.

(b) Find the probability that it rains
(i) on both days,
(ii) on Monday but not on Tuesday,
(iii) on only one of the two days.
(c) If it does not rain on Monday and it does not rain on Tuesday, the probability that it does not
rain on Wednesday is \(\frac{1}{4}\)
Calculate the probability that it rains on at least one of the three days.
Answer/Explanation
(a)

(b)(i) The probability that it rains on both days is:
Product of probabilities when it rained on monday and tuesday:
\(\frac{3}{5}\).\(\frac{4}{7}\)
= \(\frac{12}{35}\)
(ii) The probability that it rains on Monday but not on tuesday:
Product of probabilities when it rained on monday but not on tuesday:
\(\frac{3}{5}\).\(\frac{3}{7}\)
= \(\frac{9}{35}\)
(iii) The probabilities that it rains on only one of the two days:
Addition of the probability of( no rain on Monday and rain on Tuesday), and the( probability of rain on Monday and no rain on Tuesday):
P( No rain on Monday) .P( Rain on Tuesday)+P(Rain on Monday) .P(No rain on Tuesday)
\(\frac{2}{5}\).\(\frac{5}{7}\)+\(\frac{3}{5}\).\(\frac{3}{7}\)
=\(\frac{19}{35}\)
(c) Probability that it rains on at least one of the three days=P(rain on monday).P(no rain on tuesday).P(no rain on wednesday)+P( no rain on monday).P(rain on tuesday).P(no rain on wednesday)+P(no rain on monday).P(no rain on tuesday).P(rain on wednesday)
=\(\frac{34}{35}\)
Question
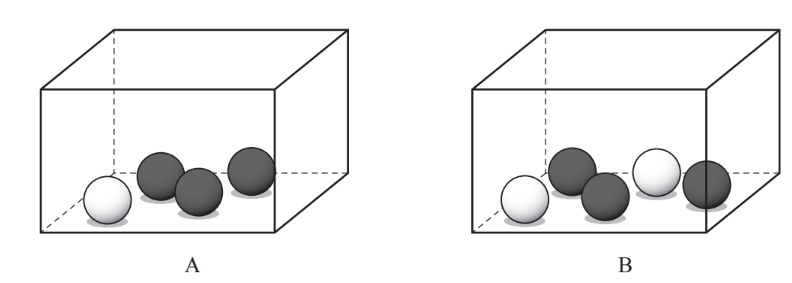
Box A contains 3 black balls and 1 white ball.
Box B contains 3 black balls and 2 white balls.
(a) A ball can be chosen at random from either box.
Complete the following statement.
There is a greater probability of choosing a white ball from Box Explain your answer.
(b) Abdul chooses a box and then chooses a ball from this box at random.
The probability that he chooses box A is $\frac{2}{3}$.
(i) Complete the tree diagram by writing the four probabilities in the empty spaces.
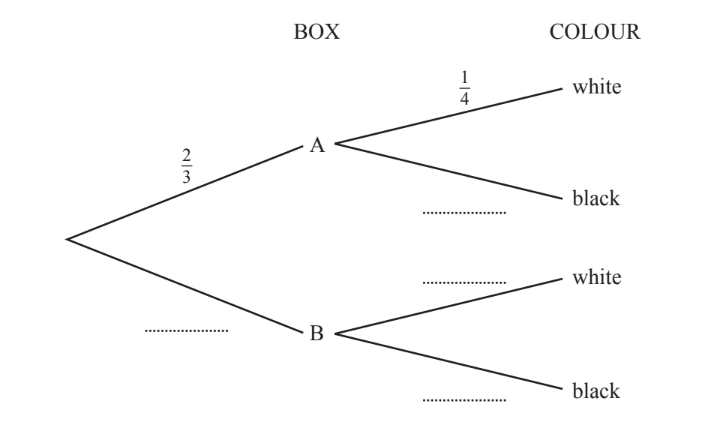
(ii) Find the probability that Abdul chooses box A and a black ball.
(iii) Find the probability that Abdul chooses a black ball.
(c) Tatiana chooses a box and then chooses two balls from this box at random (without replacement).
The probability that she chooses box $\mathrm{A}$ is $\frac{2}{3}$.
Find the probability that Tatiana chooses two white balls.
▶️Answer/Explanation
(a) $\mathrm{B}$ and $\frac{2}{5}, \frac{1}{4}$ oe
(b) (i) $\frac{1}{3}, \frac{3}{4}, \frac{2}{5}, \frac{3}{5}$
(ii) $\frac{6}{12}$ oe cao
(iii) $\frac{42}{60}$ oe cao
(c) $\frac{2}{60}$ oe cao